Движущейся жидкости

В системе из трех дифференциальных уравнений движения идеальной жидкости (56) содержится четыре неизвестных параметра движения 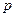; ; ; . Для того, чтобы определить эти параметры, необходимо четвертое уравнение. Таким уравнением является дифференциальное уравнение неразрывности.

Выделим в движущейся идеальной жидкости параллелепипед (рис. 21) со сторонами 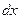; ; 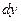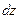, представляющий собой неподвижную часть пространства, заполненного движущейся жидкостью. Будем считать, что движение жидкости происходит без образования пустот и переуплотнений, т.е. с постоянной плотностью.

Рис. 21.

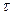В точке А в момент времени скорость движения будет 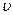, а ее проекции на координатные оси - .

Так как скорости движения частиц изменяются с изменением их положения в пространстве, то в тот же момент времени 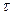скорость в точке В 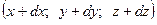, отстоящей от точки А на расстоянии 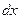будет равна 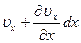. Частная производная в градиенте давления принята потому, что при переходе частицы из точки А в точку В меняется только координата .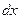

Таким образом, за время 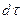через грань АСДЕ параллелепипеда будет втекать жидкость массой

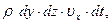
а через грань ВС₁Д₁Е₁ вытекать

.

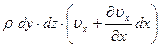Следовательно, за время 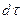изменение массы жидкости в параллелепипеде в результате движения через грани, нормальные к оси 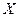будет равно

.

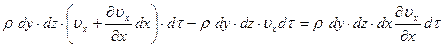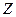Изменения массы жидкости через грани нормальные к осям и соответственно будут равны

;

.

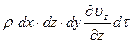Так как форма параллелепипеда остается неизменной, а движение жидкости происходит без образования пустот и переуплотнений, общая сумма изменений массы внутри параллелепипеда будет равна нулю, т.е.

или после сокращения:

(59)

Физический смысл уравнения (59) состоит в том, что сумма изменений проекций скоростей в направлении соответствующих координатных осей равна нулю. Это значит, что объем несжимаемой жидкости, которая втекает в параллелепипед, равна объему жидкости, вытекающему из него.