Закон Бернулли и его следствие

Из уравнения Эйлера для движения жидкости можно получить уравнение Бернулли в диф форме:

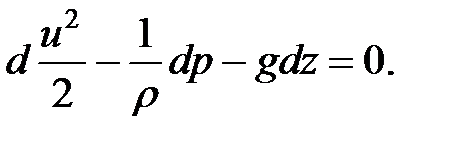
после интегрирования получаем уравнение: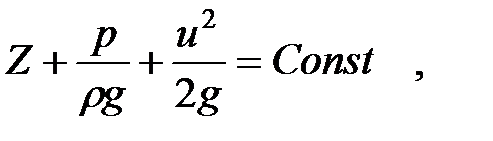

Полученное уравнение называется уравнением Д. Бернулли для элементарной струйки установившегося движения невязкой (не облад внутр трением) капельной жидкости. Вязкостью жидкостей называется свойство жидкостей оказывать сопротивление сдвигу. Все реальные жидкости обладают определенной вязкостью, которая проявляется в виде внутреннего трения при относительном перемещении смежных частиц жидкости. Вязкость капельных жидкостей в большой степени зависит от температуры; с увеличением температуры она уменьшается. Под идеальной жидкостью понимают воображаемую жидкость, обладающую абсолютной подвижностью, т.е. лишенную вязкости, абсолютно несжимаемую, не расширяющуюся с изменением температуры, абсолютно не способную сопротивляться разрыву.

В уравнение 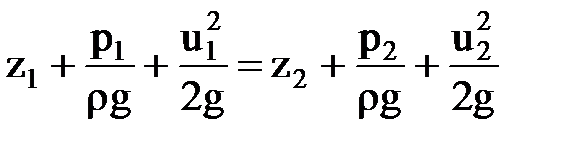входят три вида механической энергии, отнесенные к единице веса.

z₁ и z₂ – удельная энергия положения; это потенциальная энергия единицы веса, поднятой соответственно на высоту z₁ и z₂ относительно плоскости сравнения 0-0., геодезический напор.

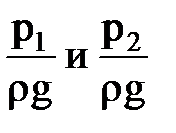– удельная энергия давления в сечениях 1-1 и 2-2 элементарной струйки идеальной жидкости, статический напор.

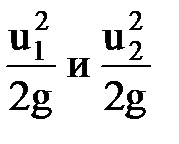– удельная кинетическая энергия; это кинетическая энергия единицы веса в соответствующих сечениях струйки, скоростной напор.

Уравнение Д. Бернулли показывает, что полная удельная энергия (энергия единицы веса) сохраняется неизменной вдоль элементарной струйки идеальной жидкости. Полный напор равен сумме всех трех напоров.

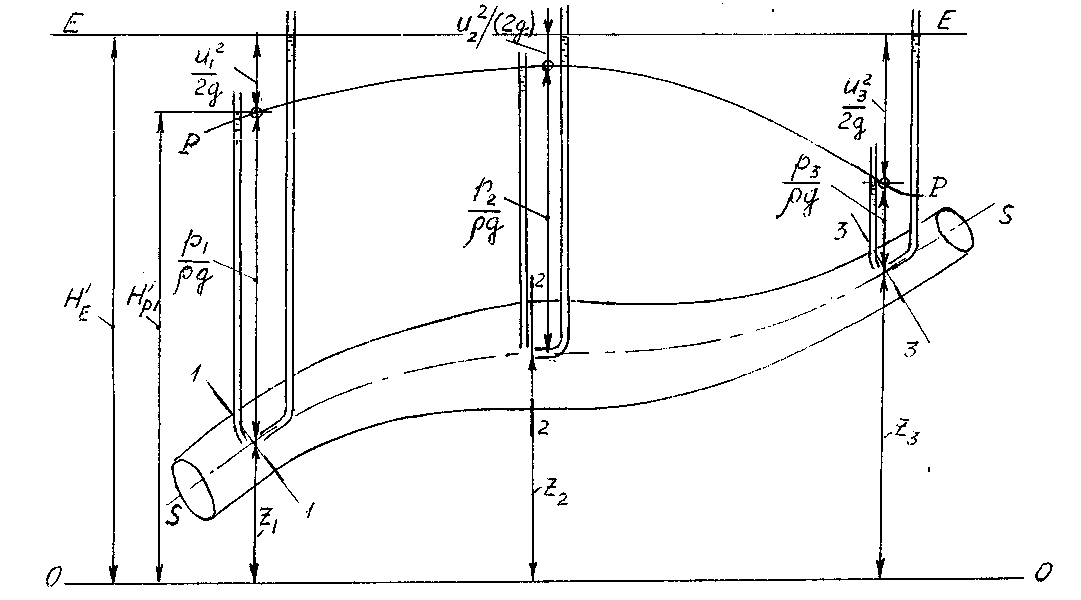Геометрическая интерпретация уравнения Бернулли для элементарной струйки идеальной жидкости

На рисунке 3. 15 приведена геометрическая интерпретация уравнения Бернулли для элементарной струйки идеальной жидкости.