Правила и образец оформления лабораторной работы
Отчет по лабораторной работе должен содержать следующие пункты.
1. Название, цель работы и данные исполнителя (титульный лист).
2. Структурная схема эксперимента или установки.
3. Таблица измеренных и рассчитанных данных.
4. Основные расчетные формулы и краткие пояснения к ним.
5. Расчет абсолютной и относительной погрешностей эксперимента.
6. Графики или диаграммы эксперимента (если требуется по заданию).
7. Запись окончательного результата и выводы по работе.
ПРИМЕР ОФОРМЛЕНИЯ ЛАБОРАТОРНОЙ РАБОТЫ
«ИЗМЕРЕНИЕ ОБЪЕМА ПАРАЛЛЕЛЕПИПЕДА»
Результаты девяти измерений длины L, высоты H и ширины Z параллелепипеда представлены в таблице измерений. При этом размеры L и Z были измерены штангенциркулем класса точности 0,1 мм, а размер H измерен микрометром класса точности 0,01 мм.
| № п/п | сред. | с.к.о. | |||||||||
| H, мм | 3,97 | 4,01 | 3,99 | 3,95 | 3,98 | 4,03 | 3,97 | 4,05 | 4,03 | ||
| DH, мм | |||||||||||
| L, мм | 39,8 | 40,1 | 40,0 | 40,1 | 40,0 | 39,9 | 40,0 | 40,1 | 40,0 | ||
| DL, мм | |||||||||||
| Z, мм | 20,1 | 20,0 | 19,9 | 20,0 | 20,0 | 20,1 | 20,0 | 20,2 | 19,9 | ||
| DZ, мм |
Инструментальные погрешности измерения длины, ширины и высоты:
°DL = °DZ = ±0,05 мм; °DH = ±0,005 мм.
Все вычисления основаны на использовании формул, приведенных в литературе [1] «Методические указания к выполнению лабораторных работ по физике для студентов биологических специальностей сельскохозяйственной академии. Механика и молекулярная физика. – Ульяновск: УГСХА, 2003».
Вычисляем средние арифметические каждой величины по формуле (3)
`H = (3,97+4,01+3,99+3,95+3,98+4,03+3,97+4,05+4,03)/9 » 4,00 мм;
`L = (39,8+40,1+40,0+40,1+40,0+39,9+40,0+40,1+40,0)/9 » 40,0 мм;
`Z = (20,1+20,0+19,9+20,0+20,0+20,1+20,0+20,2+19,9)/9 » 20,0 мм
и модули абсолютных ошибок каждого измерения по формуле (1)
DH: 0,03; 0,01; 0,01; 0,05; 0,02; 0,03; 0,03; 0,05; 0,03;
DL: 0,2; 0,1; 0,0; 0,1; 0,0; 0,1; 0,0; 0,1; 0,0;
DZ: 0,1; 0,0; 0,1; 0,0; 0,0; 0,1; 0,0; 0,2; 0,1.
После этого можно определить средние арифметические ошибки всех прямых измерений по формуле (3) и с.к.о. по формуле (7).
D`H = (0,03+0,01+0,01+0,05+0,02+0,03+0,03+0,05+0,03)/9 » 0,029 мм;
D`L = (0,2+0,1+0,0+0,1+0,0+0,1+0,0+0,1+0,0)/9 » 0,07 мм;
D`Z = (0,1+0,0+0,1+0,0+0,0+0,1+0,0+0,2+0,1)/9 » 0,07 мм.
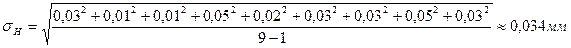
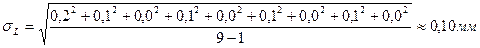

Проведенные вычисления позволяют заполнить полностью всю таблицу, которая после ее заполнения будет иметь следующий вид:
| № п/п | сред. | с.к.о. | |||||||||
| H, мм | 3,97 | 4,01 | 3,99 | 3,95 | 3,98 | 4,03 | 3,97 | 4,05 | 4,03 | 4,00 | 0,034 |
| DH, мм | 0,03 | 0,01 | 0,01 | 0,05 | 0,02 | 0,03 | 0,03 | 0,05 | 0,03 | 0,029 | |
| L, мм | 39,8 | 40,1 | 40,0 | 40,1 | 40,0 | 39,9 | 40,0 | 40,1 | 40,0 | 40,0 | 0,10 |
| DL, мм | 0,2 | 0,1 | 0,0 | 0,1 | 0,0 | 0,1 | 0,0 | 0,1 | 0,0 | 0,07 | |
| Z, мм | 20,1 | 20,0 | 19,9 | 20,0 | 20,0 | 20,1 | 20,0 | 20,2 | 19,9 | 20,0 | 0,10 |
| DZ, мм | 0,1 | 0,0 | 0,1 | 0,0 | 0,0 | 0,1 | 0,0 | 0,2 | 0,1 | 0,07 |
Для расчета суммарной абсолютной погрешности косвенного измерения объема параллелепипеда по формуле (16) необходимо предварительно определить частные производные по переменным H, L и Z.
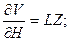
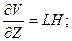
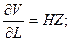
Кроме того, определяем случайные погрешности прямых измерений по формуле (14) и учитываем инструментальные погрешности, которые складываем со случайными погрешностями при подстановке в формулу (16), так как они относятся к классу аддитивных погрешностей.

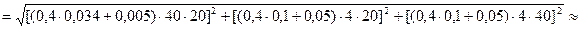
» 22 мм3.
Таким образом, с достоверностью 0,6 объем параллелепипеда, измеренный по его линейным размерам, равен: 3200 ± 22 мм3. При этом относительная погрешность измерения объема: gV = (22/3200)×100% » 0,7%.
Если принять за случайные абсолютные погрешности прямых измерений средние арифметические ошибки DH, DL и DZ (упрощенная методика расчета погрешностей), то с учетом инструментальных погрешностей, относительная погрешность измерения объема параллелепипеда будет равна:
 (»1,1%).
(»1,1%).
Из последнего вычисления видно, что расчет относительной погрешности косвенного измерения по упрощенной методике дает несколько завышенное значение, что расширяет доверительный интервал (примерно на 36%), повышая вероятность попадания истинного значения измеряемой величины в этот интервал.
В условиях учебного процесса из-за лимита учебного времени имеет смысл отдать предпочтение именно упрощенной методике расчета относительной погрешности.
Необходимо отметить, что данная упрощенная методика расчета относительной погрешности не претендует на ее использование при обработке научного эксперимента и предназначена только для учебных целей.
Дата добавления: 2015-04-15; просмотров: 1404;
