Потенциал. Разность потенциалов. Потенциал точечного заряда, диполя, сферы.

Известно, что работа сил потенциального поля может быть представлена как убыль потенциальной энергии, т. е.

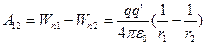. (11-25)

Отсюда следует, что потенциальная энергия пробного заряда 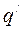в поле заряда q будет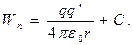

При 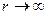потенциальная энергия должна обращаться в нуль, поэтому значение постоян­ной С полагаем равным нулю. В итоге получаем, что

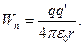(11-26)

Величину

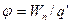(11-27)

называют потенциалом электрического поля в данной точке. Потенциал 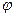, наряду с напря­женностью электрического поля 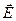, используется для описания электрического поля. Потенциал точечного заряда q, как следует из (11-26) и (11-27),

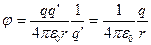, (11-28)

т. е. 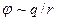(прямо пропорционален величине заряда и обратно пропорционален расстоя­нию от него). Потенциал в СИ измеряется в вольтах:

1 В= 1Дж/1 Кл.

Если поле создает система точечных зарядов 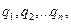то потенциал

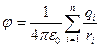. (11-29)

Из формулы (11-27) вытекает, что заряд q’, находящийся в точке поля с потенциалом 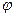, обладает потенциальной энергией

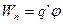. (11-30)

Следовательно, работу сил поля над зарядом q’ можно выразить через разность потен­циалов

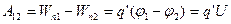,(11-31)

здесь 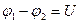- разность потенциалов между двумя точками поля, которая называется на­пряжением. Напряжение 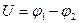тоже измеряется в вольтах.

Воображаемая поверхность, все точки которой имеют одинаковый потенциал, назы­вается эквипотенциальной поверхностью.

Ее уравнение имеет вид .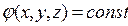

Для точечного заряда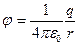

и эквипотенциальная поверхность является сферической. При перемещении заряда q’ вдоль эквипотенциальной поверхности на отрезок dl по­тенциал не изменяется, т. е. 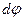= 0, следовательно,

.

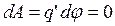Вектор напряжен­ности электрического поля 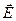, перпендикулярен эквипотенциальной поверхности.