Видимость в зрелищных помещениях

Этот метод является простейшим численным методом решения задачи Коши. Рассмотрим его на примере решения обыкновенного дифференциально­го уравнения первого порядка (6.47) с соответствующим начальным условием (6.48).

Расчетную формулу метода Эйлера можно получить, используя разло­жение функции и(х) в ряд Тейлора в окрестности некоторой точки х_i:

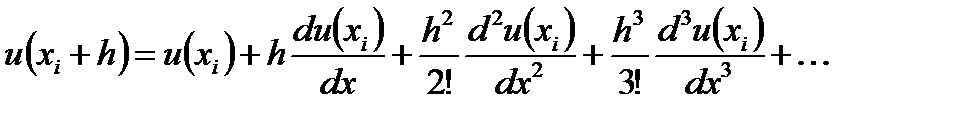(6.49)

Если приращение h мало (то есть h<<x_i), то члены ряда, начиная со слагаемого, включающего h во второй степени, могут быть отброшены как малые величины. Тогда из (6.49) в первом приближении получим:

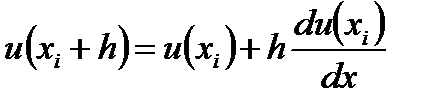(6.50)

Воспользуемся формулой (6.50), применив ее к единственной известной из условия задачи точке x₀. Найдем в х₀ производную du(x₀)/dx, подставив (6.48) в (6.47):

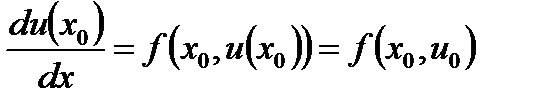
Подставив последнее выражение в (6.50) и полагая x_i = x₀, получим

u (x₀ + h) = u (x₀) + hf (x₀, u (x₀, u (x₀))

или, сокращая обозначения, в окончательном виде

u₁ = u₀ + hf (x₀, u₀)

Таким образом, (6.50) при известном значении функции u₀ = u(x₀) в на­чальной точке x₀ позволяет найти приближенное значение u₁ = u(x₁) при ма­лом смещении h от x₀. На рис. 6.2 графически показан начальный шаг решения методом Эйлера.

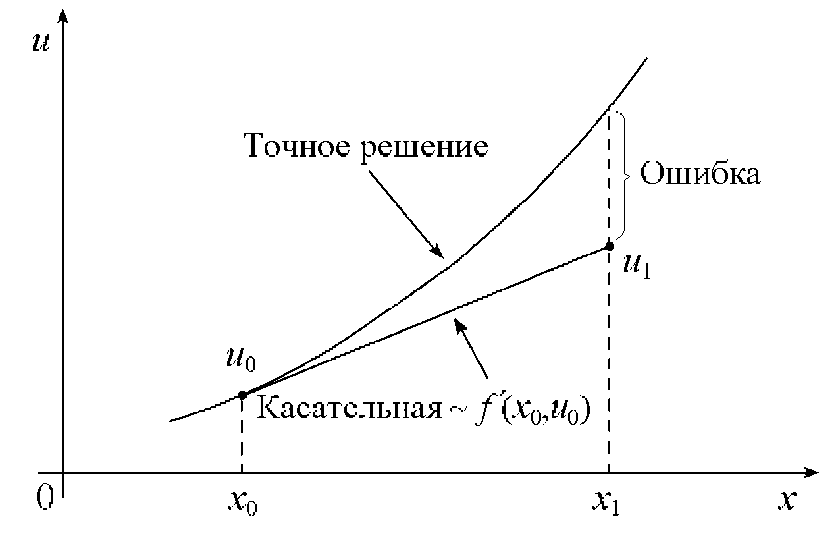
Рис. 6.2 ‑ Метод Эйлера

Решение можно продолжить, используя найденное значение функции u₁ для вычисления следующего значения - u₂. Распространяя эти рассужде­ния на последующие точки, запишем расчетную формулу метода Эйлера в виде

u_i+1 = u_t + hf (x_i, u_i), i = 0,1,2,.... (6.51)

Из рис. 6.1 видно, что ошибка метода Эйлера на шаге связана с исполь­зуемой линейной аппроксимацией u(x). Хотя тангенс угла наклона касатель­ной к кривой точного решения в точке (x₀,u₀) известен и равен du(x₀)/dx, он изменяется при смещении от x₀ до x_i. Следовательно, при сохранении начального наклона касательной на всем интервале h расчет u₁ выполняется с погрешностью.

Ошибка метода Эйлера на каждом шаге имеет порядок h², так как чле­ны, содержащие h во второй и более высоких степенях, отбрасываются - см. (6.49) и (6.50). Уменьшая h можно снизить локальную ошибку на шаге.

Видимость в зрелищных помещениях

Видимость со всех зрительных мест происходящего на сцене, эстраде, экране или арене является важнейшей задачей при проектировании помещений и зданий массового пользования (театров, кинотеатров, стадионов и др.). В зависимости от специфики зрелищных сооружений массового пользования (театр, кинотеатр или стадион) теория и метод расчета видимости при построении зрительных мест не меняется. Однако принципы, которыми руководствуются при проектировании зрительного пространства, а также нормативы видимости для театров, кинотеатров или стадионов значительно отличаются друг от друга.

К числу факторов, от которых зависит видимость в театре (кинотеатре) или стадионе, относят: объемно-пространственную структуру интерьера сооружения и его частей (сцена и зал, арена и трибуны); условия освещенности (естественные или Искусственные), а также физиологические законы зрения. Геометрический фактор видимости включает в себя следующие элементы: удаление зрителя от наблюдаемой точки; горизонтальный и вертикальный зрительные углы, определяющие положение зрителя по отношению к наблюдаемому зрелищу и, следовательно, степень зрительного искажения наблюдаемых процессов; отсутствие преград на пути зрительного луча от наблюдаемой точки к глазу зрителя.

При расчетах видимости необходимо правильно выбрать точку наблюдения зрителей. Например, для оперных театров ее обычно принимают в центре игровой площадки на уровне пола сцены, а в драматических театрах ‑ на линии портала сцены, т. е. на уровне 0,5 м от пола; в кинотеатрах такая точка расположена на нижнем краю экрана. При проектировании кинотеатров надлежит пользоваться нормами СНиП II-73‑76. Для беспрепятственной видимости выбранной точки (объекта) необходимо обеспечить условие, при котором зрительный луч (отрезок прямой, проведенный к ней от глаза наблюдателя) должен проходить на высоте с = 0,12 м над уровнем глаза впереди сидящего зрителя для кинотеатров*, крытых спортивных сооружений с - 0,12 м, открытых с = 0,15 м; с = 0,6...0,8 м ‑ для театров и концертных залов.

При с а10,12 м (для кинотеатров), если все зрелище не проглядывается между головами, возникает загораживание зрелища. Поэтому, чтобы создать равные условия видимости из всех рядов, специалисты предлагают не постоянные, а переменные превышения с для разных рядов. В последних исследованиях рекомендуют дифференцировать конкретные величины превышений с для разных рядов по разным видам зрелищ и в зависимости от расчетных координат зрителя.

АКУСТИЧЕСКИЕ ТРЕБОВАНИЯ, ОПРЕДЕЛЯЮЩИЕ ВЫБОР ОБЪЕМНО-ПЛАНИРОВОЧНЫХ РЕШЕНИЙ ЗАЛОВ С ЕСТЕСТВЕННОЙ АКУСТИКОЙ

К залам с естественной акустикой относятся: лекционные, театральные, концертные залы многоцелевого назначения средней вместимости. Деление на залы с естественной акустикой и залы, оборудованные системой звукоусиления, условно. В настоящее время практически все большие залы оборудуют звукоусилительной установкой, но при этом сохраняются требования обеспечения оптимальных акустических условий без средств звукоусиления.

Основные акустические требования, предъявляемые к данным залам, во многом сходны и зависят главным образом от объемно-планировочных решений залов.

Для залов с естественной акустикой необходимо выполнение следующих основных требований:

· обеспечение всех зрителей достаточной звуковой энергией;

· создание диффузного звукового поля, исключающего возможность образования таких акустических дефектов, как эхо и фокусирование звука;

· обеспечение оптимального времени реверберации.

Удовлетворение данных требований достигается рациональным выбором объема, геометрической формы зала, очертания его внутренних поверхностей.