Построение фрактальных изображений.

Фрактал – это самоподобный объект, у которого любая меньшая часть похожа на целый объект. Обычно фрактальные фигуры строятся с помощью рекурсивных подпрограмм. Простейшим примером фрактальной фигуры является снежинка:

Алгоритм рисования снежинки: из одной точки – центра вырастают k кристалликов-отрезков длины r, свободный конец каждого из которых служит центром новой снежинки с длиной кристаллика–отрезка, в 3 раза меньшей r. Указанный процесс продолжается n раз. Выше показаны снежинки при n=1,2 и k=6.

Для построения снежинок введем рекурсивную процедуру, параметрами которой будут координаты центра снежинок x0, y0, радиус– длина r и глубина рекурсии n. Для размещения рисунка в центре экран начальный радиус определим по формуле: , полагая dim=240, k=1/3. Получим: k=160/(1–1/3ⁿ). Координаты концов отрезка (x,y) будем находить, используя параметрическое задание уравнения окружности со смещением на заданный угол:

.

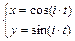Чтобы величины 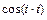и 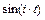не вычислялись в цикле многократно, запомним их значения в массивах C и S.

Program Sneg;

Uses Graph;

Const

k=6; {количество кристаллов}

n=5; {глубина рекурсии}

t=2*Pi/k; {угол поворота}

Var

Driver,Mode,I :Integer;

C,S :array[1..k] of Real;

Procedure Snow(x0,y0,r,m:Integer);

Var

x,y,i:Integer;

Begin

For i:=1 to k do

Begin

x:=x0+Round(r*C[i]);

y:=y0-Round(r*S[i]);

Line(x0,y0,x,y);

If m>1 then Snow(x,y,r div 3,m-1)

end;

End;

Begin

Driver:=Detect;

InitGraph(Driver,Mode,'');

For i:=1 to k do

Begin

C[i]:=Cos(i*t);

S[i]:=Sin(i*t);

end;

Snow(GetMaxX div 2,GetMaxY div 2,

Round(160/(1-1/(Exp(n*Ln(3))))),n);

ReadLn;

CloseGraph;

End.