УТЯЖЕЛЕННЫЙ НИЗ КОЛОННЫ ШТАНГ

Распределение частоты обрывов по длине колонны штанг изображается кривыми (рисунок 43).

Если кривая 1 подтверждает теоретические представления об уменьшении обрывности по мере движения к насосу за счет уменьшения нагрузки на штанги, то кривая 2 дает противоположный результат.

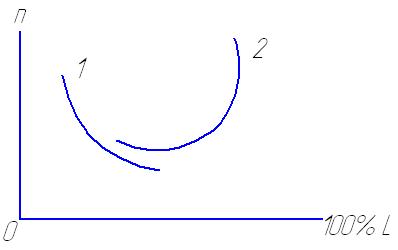
1-насос диаметром 44 мм; 2-насос диаметром 70 мм

Рисунок 43 – Распределение частоты обрывов по длине колонны штанг

Исследования позволили объяснить этот факт явлением продольного изгиба штанг, возникающим при ходе штанг вниз по причине трения плунжера о цилиндр, сопротивление при перетоке жидкости через нагнетательный клапан, трения штанг о вязкую жидкость, это нагрузка достигает 2,50 – 3,01 кН при применении насоса диаметром 68 мм.

Рассмотрим процесс изгиба штанг.

В нормальной штанге сила Р действует по оси штанги, а напряжение определяется так (рисунок 44):

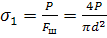(164)

где F – площадь поперечного сечения штанги.

В изогнутой штанге возникает пара сил и, следовательно, изгибающий момент. Его величина составит:

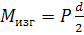(165)

где d – диаметр штанг.

Напряжение от изгиба определяется по формуле:

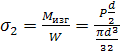(166)

где W – момент сопротивления штанги.

Суммарное напряжение от действий двух сил:

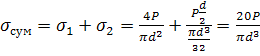(167)

Рисунок 44-Схем к расчету процесса изгиба штанг

Напряжение в изогнутой штанге 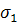в 5 раз превышает напряжение в прямой штанге 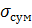. Этим и объясняется увеличение обрывности штанг в нижней части колонны.

Для исключения этого явления Фаерман И.Л. рекомендует применять утяжеленный низ штанг, массу которого можно рассчитать.

Для определения величины трения плунжера о втулку применяют эмпирическую формулу

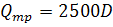, (168)

где D – диаметр плунжера в см.

Длину утяжеленного низа определяют из соотношения:

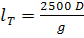, (169)

где g – вес 1 м утяжеленного низа.

Имеются таблицы, в которых рекомендуются масса и длина утяжеленного низа в зависимости от диаметра насоса.