Гидравлический расчет параллельно соединенных трубопроводов.

Трубопровод в точке А разветвляется на несколько труб, которые затем вновь объединяются в точке В; расход Q основного трубопровода до деления и после объединения труб один и тот же (рис.). Задача расчета состоит в том, чтобы определить расходы в отдельных ветвях системы Q1, Q2,…, Qn, а также потери напора hw между точками А и В. Общий расход Q диаметры и длины параллельных труб (d1, d2,…, dn; l1,l2,…,ln) предполагаются известными.

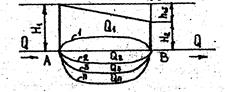
Рис. Параллельное соединение трубопроводов (1, 2, 3…n - ветви трубопроводов).

Потери напора в любой трубе ответвления одинаковы, так как в обеих общих (крайних) точках разветвления имеется, один и тот же напор H1 и общий конечный напор H2, т.e. hw=H1-H2=hw1=hw2=hw3.

Для первой ветви можно записать hw=S1Q1². Аналогично для других ветвей имеем

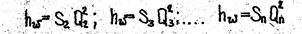
или

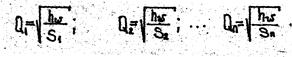(21)

Используя условие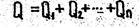

находим

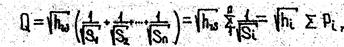
где pi=1/(Si)² - проводимость

Последнее уравнение можно переписать в виде

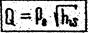
где P0=SPi.

Таким образом при параллельном соединении трубопроводов проводимости отдельных ветвей складываются.

Из последнего уравнения находим требуемый напор:

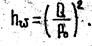
Расходы отдельных ответвлений находим по формуле (21). Так, например, для первой ветви имеем

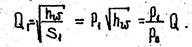
Приведенное решение получено в предположении квадратичного закона сопротивления. Для расчета параллельных трубопроводов в неквадратичной области сопротивления можно использовать поправки на неквадратичность.

Для каждой из n параллельных ветвей

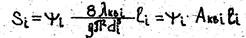
где i - порядковый номер ветви; y - поправка на неквадратичность для i-й ветви; Аквi - удельное сопротивление для i-й ветви в квадратичной области. Поправки yi вычисляем по формуле (19).

Зная поправки y, уточняем расходы в отдельных ветвях трубопровода. Так, например, для первой ветви

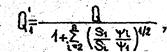
а потери напора определяются по формуле

/

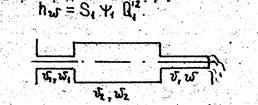
Рис. К расчету короткого трубопровода

В коротких трубах (рис.) сумма местных потерь соизмерима с потерями на трение, и расчеты таких труб ведутся с обязательным учетом потерь напора на местные сопротивления. Основная задача расчета состоит в определении пропускной способности (расхода) трубопровода. Формула для определения расхода может быть получена путем преобразования уравнения (5)

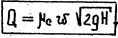(27)

где w - площадь сечения на выходе из трубы в атмосферу; m - коэффициент расхода системы, определенный из вьражения

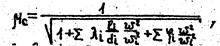(28)

В котором li, li, di, wi - соответственно коэффициенты гидравлического трения, длины, диаметра, площади сечения отдельных участков короткого трубопровода, а Vi - коэффициенты местных сопротивлений, отнесенные к скоростям в соответствующих участках.

Скорость движения на выходе из трубы в атмосферу определяется по формуле

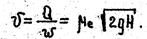
Для трубопровода постоянного сечения с имеющимися на нем местными сопротивлениями последняя формула приводится к виду

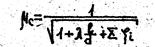
При расчете коротких труб по формулам (27) и (28) не учитывается взаимное влияние местных сопротивлений. Значения коэффициентов местного сопротивления (а часто и коэффициентов гидравлического трения) берутся по данным, относящимся к квадратичной области сопротивления.

По сравнению с движением жидкости, движение газов характеризуется некоторыми особенностями, обусловленными главным образом различием физических свойств капельных и газообразных жидкостей. При гидравлическом (аэродинамическом) расчете трубопроводов для газов следует различать два случая: движение при малых относительных перепадах давления и движение при больших перепадах (под относительным перепадом давления DP/Pср понимают отношение абсолютного перепада давления между начальным и конечным сечением DР к среднему давлена на участке Pср=(P1+P2)/2).

В первом случае (DP/Pср<5%) можно, пренебрегая сжимаемостью, считать плотность транспортируемого газа неизменной по длине трубопровода. Тогда гидравлический (аэродинамический) расчет трубопроводов для газов принципиально не отличается от расчета трубопроводов для несжимаемых жидкостей.

При больших относительных перепадах давления (DP/Pср>5%) пренебрегать сжимаемостью газа нельзя и нужно учитывать уменьшение давления транспортируемого газа по длине трубопровода, сопровождающееся снижением плотности газа с возрастанием его скорости в направлении движения.

23. Гидравлический расчет истечения жидкости через отверстия и насадки.

Истечение жидкости через отверстия и насадки является одним из главных вопросов гидравлики. Зависимости, которые установлены при изучении истечения жидкости, широко применяют в расчетах, связанных с созданием компактных струй (пожарные.брандспойты, гидромониторы), воздушных завес, наполнением и опорожнением резервуаров, бассейнов, водохранилищ, а также при разработке форм сопел, насадок и форсунок.

Экспериментально установлено, что при истечении жидкости из отверстий происходит сжатие струи в ее начальном сечении, т.е. уменьшение её поперечного сечения. Сжатие струи происходит вследствие того, что частицы жидкости подходят к отверстию с разных сторон и по инерции движутся в отверстии по сходящимся траекториям. Параллельное течение струй в отверстии возможно только в том случае, когда толщина стенок сосуда близка к размерам отверстия, а стенки отверстия имеют плавные очертания с расширением внутрь сосуда. При этом отверстие превращается в коноидальный насадок.

Отверстие считается малым, если его размер по высоте h не превышает 0,1 величины давления Н, действующего на него; средним - 0,1H<h<(0,3-0,4)H и большим - при h>0,4Н.

В зависимости от толщины стенки D отверстия классифицируют следующим образом: отверстия в тонкой стенке - D<3h; отверстия в толстой стенке - D>3h.

Отвеpстием в тонкой стенке называют отверстие, имеющее острую кромку, когда толщина стенки не влияет на форму струи и условия истечения жидкости.

У отверстия с совершенным сжатием вытекающей из него струи границы достаточно удалены от границ жидкости в резервуаре, причем стенки резервуара не оказывают влияния на условия сжатия струи. Опытом установлено, что стенки резервуара влияют на сжатие струи только тогда, когда расстояние кромок отверстия до боковой стенки или дна меньше трех диаметров для круглого отверстия или трехкратной величины сторон - для прямоугольного. Отверстием с несовершенным сжатием вытекающей из него струи жидкости называют такое отверстие, одна или несколько сторон которого находятся на близком расстоянии от поверхности жидкости или стенки резервуара.

Отверстием с полным сжатием вытекающей из него струи жидкости называют такое отверстие, в котором струя испытывает сжатие со всех сторон. В отверстии с неполным сжатием вытекающая струя не сжимается с одной или нескольких сторон. Примером такого отверстия может служить донное отверстие, в котором по дну сжатие отсутствует, а струя сжимается только с трех сторон.

Для оценки степени сжатия струи используют коэффициент сжатия струи e, под которым понимают отношение площади сжатого сечения wс к площади отверстия w:wc/w=e. Причиной, вызывающей сжатие струи, является инерционность частиц, приближающихся к отверстию резервуара по радиальным направлениям. Эти частицы, стремясь по инерции сохранить направление своего движения, огибают край отверстия и образуют поверхность струи на участке сжатия. За сжатым сечением струя практически не расширяется, а при больших скоростях истечения может распадаться на капли. Опытом установлено, что для отверстий небольших размеров с острыми кромками в случае совершенного сжатия e=0,64...0,60. Для малых отверстий (с размером стороны по вертикали не более 0,1Н) коэффициент сжатия является постоянным, тогда как в больших отверстиях он изменяется в зависимости от некоторых факторов, в том числе от напора Н перед отверстием и размеров отверстия.

Истечение жидкости через малые отверстия в тонкой плоской стенке.

В случае незатопленного отверстия (рис) считают, что напор во всех точках сжатого сечения струи одинаков. Предполагая отверстие круглым (d - диаметр отверстия), проведем плоскость сравнения О-О через центр тяжести сжатого сечения. Обозначим через H потенциальный напор или, что то же самое, заглубление центра отверстия под уровень жидкости, через vс и wс - скорость и площадь поперечного сечения струи в сжатом сечении С-С соответственно. Уравнение Бернулли для сечения 1-1 (уровень свободной поверхности) и сжатого сечения струи С-С имеет вид:

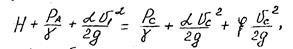
где v1 и vс - средние скорости в соответствующих сечениях; V - коэффициент сопротивления, учитывающий потери напора от сечения 1-1 до сечения С-С (потери сосредоточены главным образом в районе отверстия).

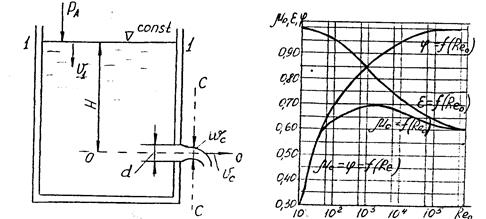
Рис. 1 - Схема истечения жидкости в атмосферу через малое отверстие в тонкой стенке

2 - график А.Д. Альтшуля

После преобразования уравнения Бернулли получим формулу средней скорости для идеальной жидкости vс=(2gh)^0,5 – формула Торичелли, а так же формулу расхода жидкости, проходящего через отверстие.

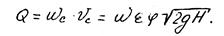
Обозначив m0=ej, формулу расхода жидкости в случае истечения через малое отверстие получим в виде

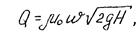
где m0 - коэффициент расхода отверстия, который показывает, насколько действительный расход жидкости при истечении из отверстия уменьшается по сравнению с теоретическим расходом в идеальном случае, т.е. при истечении идеальной жидкости без сжатия струи.

Обычно коэффициенты m0 и e определяют опытным путем, а коэффициент j находят путем вычислений.

Коэффициент сопротивления V выражают через коэффициент скорости:

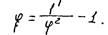
Коэффициент истечения жидкости зависит от числа Рейнольдса. На рис. приведены кривые (график А.Д. Альтшуля) зависимости коэффициентов m0, j и e от числа Рейнольдса для случая истечения жидкости из малого отверстия в тонкой стенке. С увеличением Re коэффициент скорости j возрастает, приближаясь к 1, а e уменьшается от I до 0,6. Коэффициент m0 вначале возрастает, а затем уменьшается.

При истечении жидкости из малого отверстия в тонкой стенке под уровень расход жидкости в сжатом сечении при истечении через затопленное отверстие

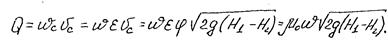
Коэффициент расхода m0 при истечении из затопленных отверстий имеет примерно такое же значение, как и при истечении в атмосферу.

Истечение жидкости через большие отверстия в тонкой плоской стенке при постоянном напоре.

Если при истечении жидкости через малое отверстие можно было принимать, что напор Н в пределах отверстия постоянен, то в случае больших отверстий напор в пределах их сечений изменяется от H1 в верхней части отверстия до H2 в нижней. Для определения расхода жидкости через большое отверстие с учетом переменного напора по глубине разбивают площадь поперечного сечения отверстия на полоски высотой dH. Каждую из полосок рассматривают как малое отверстие с постоянным напором H и расходом

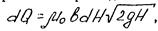
где b - ширина большого отверстия прямоугольного сечения; m0 - коэффициент расхода малого отверстия; H - напор для малого отверстия.

Принимая m0=const получают расход жидкости, проходящей через большое отверстие:

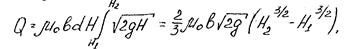
где H1 и H2 - пределы интегрирования.

Окончательная формула расхода жидкости при истечении через большое отверстие примет вид:

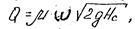
где Hс – превышение горизонта воды в сосуде над центром тяжести большого отверстия; m0 - коэффициент расхода большого отверстия. Большие значения m0 относятся к отверстиям с плавными боковыми и донными подходами к ним.

Истечение жидкости через насадки.

Насадками называют короткие трубы, имеющие различные формы живого сечения и постоянные или меняющиеся размеры основного канала по длине. Длину насадков обычно принимают равной трем – пяти характерным размерам живого сечения. Насадки применяют для измерения расхода жидкости, организации направленного слива, создания струй фонтанных, пожарных, гидромониторных и др. Воздействием струй воды приводят во вращение колеса ковшовых гидротурбин, струями высокого давления разрушают твердые горные породы, режут металлы и т.д.

Поток жидкости, поступающий в насадок, в большинстве случаев отрывается от стенки насадка у входа, сужается, расширяется и вновь касается у выхода. Область отрыва заполнена завихренной массой жидкости. В этой области создается пониженное давление, что увеличивает действующий напор, и поэтому коэффициент расхода насадков выше, чем отверстий (рис.).

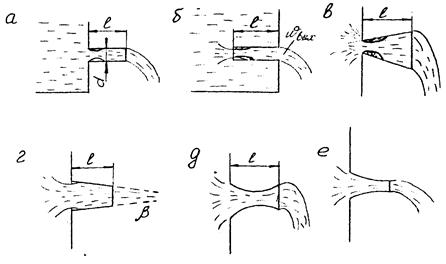
Рис. Виды насадков: а - внешний цилиндрический (Вентури); б - внутренний цилиндрический (Борда); в – конически расходящийся; г - конически-сходящийся; д - коноидально-расходящийся; е – коноидальный.

Насадок с хорошо закругленными краями (мерное сопло) – наиболее распространенная форма насадка, применяемого для определения расхода жидкости. Фланец насадка заподлицо с днищем устанавливают в мерную емкость. Это мерное устройство называют данаидой. Радиус закругления в насадках принимают равным R=(З...4)d; протяженность цилиндрической части составляет l=0,25d. Такое очертание насадка обеспечивает выход струи без сжатия, т.е. e=1. Коэффициент расхода калиброванного насадка, изготавливаемого из металла, не подвергающегося коррозии, вполне стабилен.

Расход жидкости при помощи данаиды определяют по формуле:

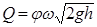
Для насадка Вентури после соответствующих преобразований получим следующие соотношения.

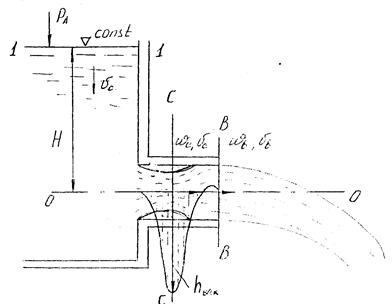
Рис. Схема насадка Вентури.

Скорость потока при выходе из насадка

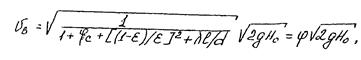
где j - коэффициент скорости для насадка,

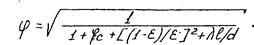
Расход жидкости, проходящей через цилиндрический насадок,

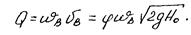
Так как в области выхода потока насадок работает полным сечением, то коэффициент сжатия e=1. Поэтому коэффициент расхода жидкости через насадок равен коэффициенту скорости: mн=j.

Следует заметить, что увеличение длины патрубка приводит к возрастанию V и, соответственно, к уменьшению коэффициента расхода насадка. Поэтому для цилиндрических насадков обычно принимают длину l=(3...4)d, при которой насадок еще работает полным сечением с образованием вакуума, причем величиной V пренебрегают. В случае меньшей длины насадка струя не успевает расширяться до полного её сечения и истечение будет происходить как из отверстия в тонкой стенке. Значения коэффициентов для насадков различных типов можно принимать по табл.

Последняя формула справедлива для насадков всех типов, а также для отверстий в толстой стенке.

Увеличение пропускной способности насадка в сравнении с отверстием происходит за счет образования вакуума в сжатом сечении.

Расход жидкости, проходящей через насадок ,

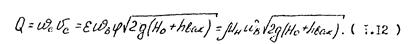
Заменив в зависимости (I2) hвак на 0,75H0 получим

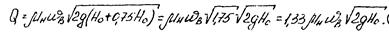
Сравнивая эти формулы для расхода жидкости через малое отверстие, можно сделать вывод, что в результате образования вакуума пропускная способность цилиндрического насадка увеличивается по сравнению с малым отверстием того же диаметра в тонкой стенке.

В конически расходящихся насадках в области сжатого сечения создается вакуум, как и в цилиндрических насадках, но большей величины. При этом величина вакуума возрастает с ростом угла конусности. При большом угле конусности возможен отрыв струи от стенок насадки и, следовательно, срыв вакуума. Опытом установлено, что оптимальный угол конусности составляет 5-7°. Конически расходящиеся насадки из-за расширения потока отличаются от всех других насадков значительными потерями напора. Расходящиеся насадки имеют малые скорости выхода вследствие увеличения площади поперечного сечения потока.

Конически сходящиеся насадки используют для увеличения скорости выхода жидкости, т.е. создания струй, обладающих большой удельной кинетической энергией. Струи, выходящие из таких насадков, отличаются компактностью и способностью на длительном расстоянии сохранять свою форму, не распадаясь на отдельные капли. Коэффициент расхода насадка зависит от угла конусности и достигает своего максимального значения при угле 13°24', так как в этом случае площадь сжатого сечения оказывается равной площади выходного сечения. При дальнейшем увеличении угла конусности затрачивается энергия на сжатие струи при выходе из насадка и в связи с этим уменьшается коэффициент расхода.

Коноидальный насадок представляет собой усовершенствованный сходящийся насадок. Он выполняется по форме струи жидкости, вытекающей из отверстия, что устраняет сжатие струи и сводит до минимума потери напора.

Явления, происходящие во внутреннем и внешнем цилиндрическом насадке (насадке Борда), аналогичны. Условия входа жидкости в нём несколько хуже вследствие большего изгиба линий тока, поэтому коэффициент расхода внутреннего насадка несколько меньше, чем внешнего.

24. Гидравлические сопротивления при обтекании твердого тела потоком жидкости или газа.

Суммарное сопротивление при обтекании твердого тела.

В общем случае сопротивление при обтекании твердого тела потоком жидкости или при движении твердого тела в жидкость представляет собой сумму сопротивлений трения и сопротивлений давления. Суммарное или полное сопротивление (лобовое сопротивление обычно определяется по формуле, структура которой предложена ещё Ньютоном:

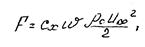
где cx - коэффициент лобового сопротивления, зависит от формы тела, Re и, в несколько меньшей степени, от степени турбулентности невозмущенного потока.

Зависимости cх от Re получают экспериментально для конкретного тела.

Для твердых тел с резко меняющимся профилем (диски, пластины, расположенные поперек потока кубы, профили зданий и т.п.) коэффициент лобового сопротивления практически не зависит от числа Re. Опытным путем установлена экспериментальная зависимость cx=f(Re) для различных условий движения шаров в жидкости, представленная в логарифмических координатах (рис.).

Изменение числа Re влечет за собой изменение соотношения между действующими на тело силами трения, инерции и давления (рис.) Причем увеличение Rе приводит к уменьшению влияния сил трения и повышению влияния сил инерции и давления. Кроме того, при изменении Rе меняется положение точки отрыва пограничного слоя и его структура. До тех пор, пока пограничный слой остается ламинарным (10<Rе<10³), точка отрыва находится в лобовой части сферы (рис. а).

При 10³<Re<10⁵ ламинарный пограничный слой постепенно переходит в турбулентный и точка отрыва смещается в кормовую область (рис. б).

В этом диапазоне чисел Rе сопротивление увеличивается за счет возрастания действия разности давлений перед шаром и за ним. Кривая cx=f(Re) приближается к горизонтали. Полный переход ламинарного пограничного слоя в турбулентный происходит при Re=Reкр=10⁵. В этом случае угол a»110-120° и величина области отрывного течения становится наименьшей (рис. в). Сопротивление резко уменьшается, такое давление называется кризисом сопротивлений.

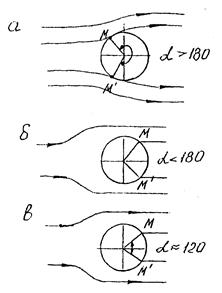
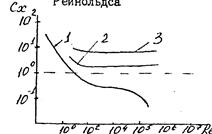
Рис. 1-Изменение положения точки отрыва пограничного слоя на сфере при различных числах Рейнольдса 2-зависимость коэффициента лобового сопротивления от числа Рейнольдса (1-шар, 2-цилиндр, 3-диск).

Для твердых тел с резко меняющимся профилем (диски, пластины, расположенные поперек потока, кубы, некоторые профили зданий) коэффициент лобового сопротивления практически не зависит от числа Re.

25. Скорость витания, методы ее расчета, практическое значение.

При свободном падении твердой частицы в жидкой или газовой среде, находящейся в покое, только в первый момент наблюдается ускоренное движение; в дальнейшем возникающая сила сопротивления уравновешивается действием силы тяжести и частица падает равномерно, с постоянной скоростью. Эта скорость называется гидравлической крупностью. Это понятие имеет большое значение при изучении процессов взвешивания и отстаивания в жидкости, а также для расчета трубопроводов для гидротранспорта частиц.

При изучении аналогичных процессов в воздушной среде используется понятие скорости витания. Под последней понимают скорость восходящего потока воздуха (в вертикальной трубе), при которой твердые частицы, находящиеся в этом потоке, будут совершать колебательные движения приблизительно на одном уровне (как бы витать), т.е. будут находиться во взвешенном состоянии. Иначе говоря, это понятие эквивалентно гидравлической крупности применительно к воздушной среде.

Выведем формулу скорости витания частицы шарообразной формы.

Сила тяжести частицы (или её вес)

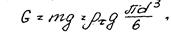
где r_t - плотность частицы.

В воздушной среде частица падает под действием силы G¢, меньшей чем G, вследствие влияния архимедовой силы А.

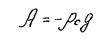
где r0 - плотность воздуха.

Таким образом, сила падения

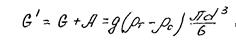
Сила сопротивления при падении частицы в воздухе

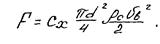
Так как эти силы уравновешиваются при равномерном падении, то

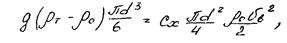
откуда

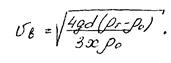(21)

Поскольку плотность воздуха r0 значительно меньше плотности rт транспортируемого материала, разность rт-r0 без большой ошибки можно заменить на rт. Тогда формула для скорости витания шарообразной частицы принимает вид

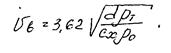
Итак, зная коэффициент сопротивления частицы cx, нетрудно по формуле определить скорость витания. Так как значения cx в свою очередь, зависят от скорости, задача решается методом подбора.

Для частиц определенной формы коэффициент лобового сопротивления зависит только от числа Рейнольдса, поэтому уравнение равномерного осаждения (всплывания) твердых частиц можно представить в виде зависимости числа Рейнольдса от критерия Архимеда:

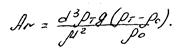
При Re<2 скорость витания определяется по уравнению Стокса:

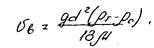
Для области действия закона Стокса (Ar<=36) используется зависимость

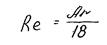
Для переходной области, где 2<Rе<500, что соответствует изменению критерия Ar в пределах 36<Ar<83000,

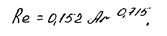
Для автомодельной области, где Ar>83000

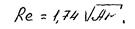
Для расчетов может быть использована и единая интерполяционная зависимость, связывающая критерии Re и Ar для всех режимов осаждения:

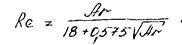
Таким образом, рассчитав критерий Ar, определяют по его значению область, в которой происходит осаждение. Вычисляют, пользуясь одним из уравнений, отвечающим этой области, значение Re и находят по нему скорость осаждения

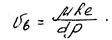
В практических условиях форма твердых частиц, концентрация и характер транспортируемого материала различны. Поэтому, чтобы получить конкретные данные для расчета, скорость витания различных материалов определяют экспериментальным путем в специальной трубе витания. Она изменяется в широких пределах - от 2 до 12 м/с.

Для обеспечения пневмотранспорта твердых материалов среднюю скорость движения воздуха в трубопроводе берут несколько большей (в зависимости от формы частиц и концентрации материала) скорости витания, определенной для шаровидной частицы по формуле (21).

Понятие скорости витания по существу относится к вертикальным участкам трубопроводов пневмотранспорта. На горизонтальных участках условия для перемещения твердых частиц иные.

Рассмотрим механизм перемещения твердых частиц в горизонтальной трубе (рис.). Возьмем шаровидную частицу, расположенную на дне трубы. При обтекании шара, как и при обтекании цилиндра, вверху частицы вследствие увеличения скорости образуется область пониженного давления и возникает подъемная сила P, которая при достаточной скорости поднимает частицу. Сила сопротивления F перемещает частицу в направлении движения воздуха в трубе, а сама частица начинает вращаться (в данном случае по часовой стрелке) в результате эффекта вязкостного трения. В дальнейшем, когда частица поднялась, действие подъемной силы Р прекращается,| но вращение частицы благодаря инерции и наличию поперечного градиента осредненных скоростей сохраняется. Последнее образует циркуляцию и соответствующую ей подъемную силу Pу (эффект Магнуса). Эта сила, как правило, недостаточна для поддержания частицы во взвешенном состоянии. Поэтому частица, описав некоторую траекторию, падает на дно трубы и описанное явление повторяется.

В результате частицы движутся в воздушном потоке, описывая сложные, а после поворота, трубы - винтовые траектории. Средняя скорость потока воздуха, при которой частицы начинают двигаться указанным образом в горизонтальной трубе, называется скоростью веяния.

Если весьма увеличить скорость течения воздуха, то можно добиться того, что твердые частицы будут перемещаться в горизонтальном трубопроводе, не падая на дно, т.е. будут находиться во взвешенном состоянии. Такая способность турбулентного потока объясняется наличием в нем поперечных пульсаций. Однако осуществлять пневмотранспорт таким образом вследствие большой разницы плотностей воздуха и материала экономически нецелесообразно, а в некоторых случаях даже невозможно. Наоборот, гидротранспорт, где разность плотностей материала и воды в большинстве случаев незначительна, осуществляется при таких скоростях течения воды, когда частицы находятся во взвешенном состоянии.

Скорость веяния по абсолютной величине мало отличается от скорости витания. Поэтому на практике расчет пневмотранспорта ведут по скорости витания.

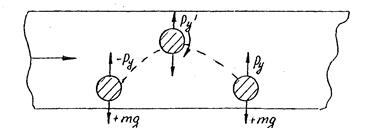
Рис. Механизм перемещения твердых частиц потоком воздуха в горизонтальном направлении

26. Классификация нагнетателей (насосов, вентиляторов). Особенности рабочих процессов динамических и объемных нагнетателей. Основные рабочие параметры, напорные характеристики.

Гидравлической машиной называют устройство, преобразующее механическую работу в энергию потока жидкости и наоборот. Гидравлическая машина, в которой в результате обмена энергией происходит преобразование механической энергии жидкости в механическую работу (вращение вала, возвратно-поступательное движение поршня и т. д.), называется турбиной или гидродвигателем. Гидравлическая машина, в которой происходит преобразование механической работы в механическую энергию жидкости, называется нагнетателем. К нагнетателям относятся насосы и воздуходувные машины. Воздуходувные машины служат для повышения давления и подачи воздуха или другого газа. В зависимости от степени сжатия воздуходувные машины разделяют на вентиляторы и компрессоры.

Вентилятор - воздуходувная машина, предназначенная для подачи воздуха или другого газа под давлением до 15 кПа при организации воздухообмена.

Компрессор - воздуходувная машина, предназначенная для сжатия, и подачи воздуха и какого-либо газа под давлением не ниже 0,2 MПа.

Насос - устройство, служащее для напорного перемещения (всасывания, нагнетания) главным образом капельной жидкости, в результате сообщения ей энергии.

Основное назначение нагнетателя - повышение полного давления перемещаемой среды. В зависимости от свойств среды (газ, чистая жидкость, загрязненная жидкость и взвесь, вязкая жидкость, агрессивная жидкость, жидкий металл, сжиженный газ и т. п.) применяются нагнетатели различных типов и конструкций. В практике довольно часто встречаются нагнетатели разных типов, названия которым даны в зависимости от их назначения и особенностей эксплуатации (например, питательные, циркуляционные, конденсатные насосы для тепловых электростанций и т.п.). Нагнетатели в основном классифицируют по принципу действия и конструкции. В этом смысле их подразделяют на объемные и динамические.

Объемные нагнетатели работают по принципу вытеснения, когда давление перемещаемой среды повышается в результате сжатия. К ним относятся возвратно-поступательные (диафрагменные, поршневые) и роторные (аксиально- и радиально-поршневые, шиберные, зубчатые, винтовые и т. п.) насосы.

Динамические нагнетатели работают по принципу силового воздействия на перемещаемую среду. К ним относятся лопастные (радиальные, центробежные, осевые) нагнетатели и нагнетатели трения (вихревые, дисковые, струйные и т.п.).

Нагнетатели используемые в системах теплогазоснабжения и вентиляции, должны удовлетворять следующим основным требованиям:

1) соответствие фактических параметров работы (p, L и N) заданным расчетным условиям;

2) возможность регулирования подачи и давления в определенных пределах;

3) устойчивость и надежность в работе;

4) простота монтажа;

5) бесшумность при работе.

Из группы динамических насосов самое широкое распространение получили центробежные насосы (лопастные), которые применяются в системах водоснабжения, отопления, в технологических процессах.

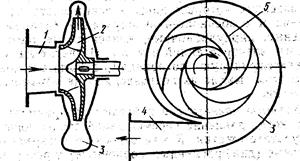
Рис. Схема центробежного насоса

1-входной патрубок; 2-рабочее колесо; 3-корпус; 4-нагнетательный патрубок; 5-лопатка

К основным параметрам работы нагнетателей относятся: подача, напор, мощность, КПД нагнетателя.

Подача – объем жидкости, подаваемой нагнетателем в единицу времени. Из определения следует, что расход жидкости, проходящей в трубопроводе, равен подаче нагнетателя, сообщающего этой жидкости движение. Подача насоса - Q, м³/с, подача вентилятора – L, м³/с (м³/ч).

Напор (давление). Напор нагнетателя - понятие энергетическое. Напор насоса представляет собой энергию, сообщенную единице веса жидкости, прошедшей через насос (H). Давление вентилятора представляет собой энергию, сообщенную единице объема газа, прошедшего через вентилятор (P).

Мощность – энергия, сообщаемая или затрачиваемая в единицу времени. Полезная мощность потока жидкости, выходящей из нагнетателя N=QH. Полезная мощность газа, выходящего из вентилятора N=LP.

В любой насосной или вентиляторной установке мощность в различных ее узлах не одинакова. Т.к. мощность на валу меньше, чем мощность электрическая, из-за потерь при работе электродвигателя, то необходимо учитывать КПД электродвигателя Nв=Nэhэ.

Т.о. нагнетателю подается мощность на валу – потребляемая нагнетателем мощность. Полезная мощность нагнетателя меньше, чем мощность на валу, на величину потерь мощности в нагнетателе. Эти потери мощности учитываются КПД нагнетателя Nп=Nвhн.

Потери мощности в нагнетателе подразделяют на гидравлические, объемные и механические.

Механическими являются потери мощности на различные виды трения в рабочем органе нагнетателя.

Объемные потери возникают в результате утечек жидкости через уплотнения в нагнетателе, а также перетоков из областей высокого давления в области низких, обусловленных особенностями конструкций.

Гидравлический КПД учитывает потери, которые возникают вследствие наличия гидравлических сопротивлений в подводе, рабочем колесе и отводе.

Характеристики работы насоса изображаются на специальном графике, по которому можно определять параметра работы нагнетателя в конкретной сети. При этом определяется будут ли в сети необходимые значения характеристик при использовании данного нагнетателя.

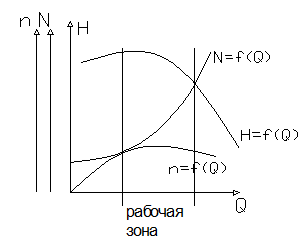
Рис. Характеристики работы насоса.