Й блок.

15. Уравнение неразрывности движения капельных и газообразных жидкостей, его практическое значение.

Основным условием, которое должно соблюдаться при течении жидкости или газа, является непрерывность изменения параметров потока в зависимости от координат и времени, т.е. условие сплошности. Это значит, что жидкость или газ должны двигаться в соответствующих каналах как сплошная среда без разрывов.

Условие неразрывности или сплошности для элементарной струйки имеет вид

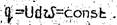
Это уравнение распространяется и на поток с конечным поперечным живым сечением, который представляет собой совокупность бесконечного множества элементарных струек

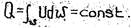
U - скорость элементарной струйки.

Заменим U на среднюю скорость V.

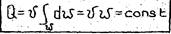
Отсюда следует, что при условии неразрывности расход вдоль потока есть величина постоянная. Если

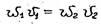или

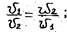
то есть отношение средних скоростей в различных сечениях потока обратно. пропорционально площади живых сечений, вдоль трубки тока масса жидкости остается постоянной.

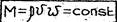
т. е. для сжимаемых жидкостей rvw=const.

Если выразить скорость линий тока через её проекции на координатные оси, то уравнение неразрывности будет иметь вид

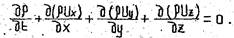
Если течение, установившееся, то условие сохранения сплошности течения можно представить следующим образом:

Когда жидкость, кроме того, еще и несжимаемая, то r=const и тогда

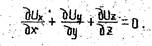
16. Уравнение Бернулли для потока вязкой жидкости. Его геометрический и энергетический смысл.

Решение уравнений движения Эйлера для установившегося потока приводит к одному из наиболее важных и широко используемых уравнений гидродинамики - уравнению Бернулли.

Уравнение Бернулли для идеальной жидкости:

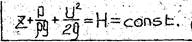
Для двух поперечных сечений 1 u 2 потока имеем

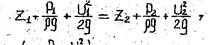
величину 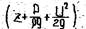называют полным гидродинамическим напором или просто – гидродинамическим напором H.

Формулировка уравнения Бернулли: для всех поперечных сечений установившегося потока идеальной жидкости гидродинамический напор остается неизменным.

Гидродинамический напор включает следующие слагаемые: Z - нивелирная высота, называемая геометрическим или высотным напором (м), представляет собой удельную потенциальную энергию положения в данной точке; P/rg - напор давления или пьезометрический напор, характеризует удельную потенциальную энергию давления в данной точке. Сумма (Z+P/rg), называемая гидростатическим или просто - статическим напором (hсm), выражает полную удельную потенциальную энергию в данной точке. Величины Z и P/rg могут быть выражены как в единицах длины, так и в единицах удельной энергии, то есть энергии, приходящейся на единицу веса жидкости. Величину U²/2g называют скоростным или динамическим напором hск. Скоростной напор характеризует удельную кинетическую энергию в данной точке (сечении).

Таким образом, согласно уравнению Бернулли, при установившемся движении идеальной жидкости сумма скоростного и статического напоров, равная гидродинамическому напору, не меняется при переходе от одного поперечного сечения потока к другому.

Вместе с тем из уравнения Бернулли в соответствии с энергетическим смыслом его членов следует, что при установившемся движении идеальной жидкости сумма потенциальной (Z+P/rg) и кинетической (U²/2g) энергии жидкости для каждого из поперечных сечений потока остается неизменной.

При изменении поперечного сечения трубопроводов и, соответственно, скорости движения жидкости происходит превращение энергии: при сужении трубопровода часть потенциальной энергии давления переходит в кинетическую и наоборот, при расширении трубопровода часть кинетической энергии переходит в потенциальную, но oбщee количество энергии остается постоянным. Отсюда следует, что для идеальной жидкости количество энергии, поступающей с потоков через начальное сечение трубопровода равно количеству энергии удаляющейся с потоком через конечное сечение трубопровода. Таким образов, уравнение Бернулли является частным случаем закона сохранения энергии и выражает энергетический баланс потока.

Проиллюстрируем применение уравнения Бернулли на примере потока идеальной жидкости, движущейся через произвольно расположенный в пространстве трубопровод переменного сечения.

Пусть для точек, лежащих на оси трубопровода в поперечных сечениях I-I и 2-2, нивелирные высоты равны Z1 и Z2 соответственно. Установим в каждой из этих точек две вертикальные пьезометрические трубки, у одной из которых нижний конец загнут навстречу потоку жидкости в трубопроводе.

В прямых вертикальных трубках (с незагнутыми нижними, концами) жидкость поднимается на высоту, отвечающую гидростатическому давлению в точках их погружения, то есть эти трубки будут измерять пьезометрические напоры в соответствующих точках.

.

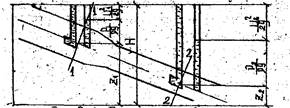
Рис. Геометрическая интерпретация уравнения Бернулли для потока невязкой жидкости

В трубках с нижними концами, направленными навстречу потоку, уровень жидкости будет выше, чем в соседних трубках, так как трубки с загнутыми концами будут показывать сумму пьезометрического и динамического (скоростного) напоров. Однако согласно уравнению Бернулли, во все.х трубках с загнутом нижними концами жидкость поднимается на одну и ту же высоту относительно произвольной горизонтальной плоскости сравнения, равную гидродинамическому напору Н.

Площадь поперечного сечения 2-2 трубопровода меньше сечения 1-1. Поэтому скорость жидкости U2 при данном ее расходе, согласно уравнению неразрывности потока, будет больше U1.

В любом поперечном сечении трубопровода скоростной напор можно измерить по разности показаний установленных здесь трубок (с загнутыми и прямыми нижними концами). Следовательно, эта разность должна быть больше для сечения 2-2, чем для сечения I-I.

Вместе с тем из уравнения Бернулли следует, что высота уровня жидкости в прямой трубке в сечении 2-2 должна быть меньше соответствующей высоты в прямой трубке сечения 1-1 на столько же, на сколько скоростной напор в сечении 2-2 больше, чем в сечении 1-1.

Приведенный пример демонстрирует взаимный переход потенциальной энергии в кинетическую при изменении площади сечения трубопровода, а также постоянство этих энергий в любом поперечном сечении трубопровода, соответственно

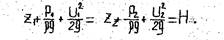
При движении реальных жидкостей начинают действовать силы внутреннего трения, обусловленные вязкостью жидкости и режимом её движения, а также силы трения о стенки трубы. Эти силы оказывают
сопротивление движению жидкости. На преодоление возникающего гидравлического сопротивления должна расходоваться некоторая часть энергии потока. Поэтому oбщee количество энергии потоке по длине трубопровода будет непрерывно уменьшаться вследствие перехода потенциальной энергии в потерянную энергию, затрачиваемую на трение и безвозвратно теряемую при рассеивании тепла в окружающую среду.

При движении реальной жидкости высоты её подъема (относительно плоскости сравнения) в трубках с концами, обращенными навстречу потоку, уже не будут равны в сечениях I-I и 2-2, как для идеальной жидкости. Разность высот в этих трубках, обусловленная потерями энергии не пути жидкости от сечений I-I и 2-2, характеризует потерянный напор hп.

Для соблюдения баланса энергии, при движении реальной жидкости, в правую часть уравнения Бернулли должен быть введен член, выражающий потерянный напор. Тогда уравнение .Бернулли для элементарной струйки реальной жидкости будет иметь вид

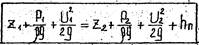
Потерянный напор hп характеризует удельную (то есть отнесенную к единице веса жидкости) энергию, расходуемую на преодоление гидравлического сопротивления при движении реальной жидкости.

После умножения, членов уравнения, на rg, имеем

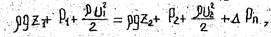
где 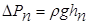- потери давления.

Определение потери напора или давления необходимо при расчетах энергии, затраченной на перемещение реальных жидкостей при помощи насосов, компрессоров и т.д.

В практических расчетах уравнение Бернулли для струйки реальной жидкости распространяют на целый поток реальной жидкости, состоящий из множества струек. При этом учитывают, что поток реальной жидкости ограниченный стенками имеет неравномерное распределение скоростей по сечению и потери энергии (напора) вдоль потока.

Неравномерность распределения скоростей по сечению движущейся вязкой жидкости объясняется торможением потока вдоль стенок из – за действия сил молекулярного сцепления между жидкостью и стенкой. Использование для расчета удельной кинетической энергии средней по сечению скорости приводит к ошибке, которая .может быть скорректирована введением поправочного коэффициента a (коэффициента Кориолиса).

С учетом вышеизложенного уравнение Бернулли для потока реальной жидкости примет вид

где Shп - суммарные потери напора на участке 1-2.

После умножения членов уравнения на rg имеем

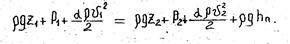или

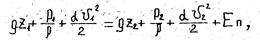
где 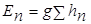- потери удельной энергии отнесенные к единице массы потока на преодоление сопротивлений на рассматриваемом участке.

Эти уравнения называются уравнением баланса удельных энергий реального потока с учетом потерь. Все члены уравнения имеют тот же геометрический и энергетический смысл, что и уравнение Бернулли для элементарной струйки реальной жидкости, из последнего уравнения следует, что удельная энергия Eп затраченная на преодоление сил трения, равна изменению полной удельной энергии потока на том же участке (рис.).

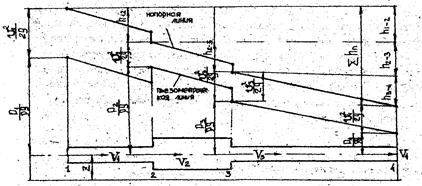
Рис. Графическое представление уравнения Бернулли для реального потока.

Согласно уравнению Бернулли имеем:

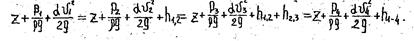
Коэффициент Кориолиса a (или коэффициент кинетической энергии) представляет собой отношение действительной удельной кинетической энергии потока к энергии, подсчитанной по средней скорости

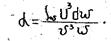
Уравнение Бернулли для газов в дифференциальной форме имеет вид

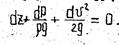
Для газов, обладающих вязкостью, необходимо учитывать потери энергии на сопротивления, поэтому для элементарной струйки имеем

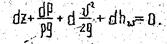
Интегрируя это выражение для элементарной струйки получим

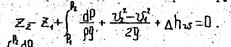
Из уравнения политропы

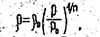
тогда уравнение Бернулли имеет вид

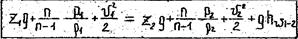
Так как уравнение состояния газов

то

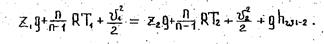
При адиабатическом процессе n=k,. поэтому

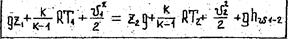
При изотермическом процессе

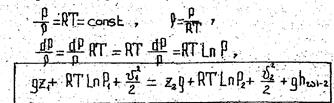
Рассмотрим неустановившийся поток жидкости в канале, ограниченном неподвижными стенками. Выберем два сечения.

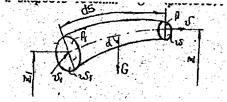
Рис. Течение жидкости в трубке тока в момент времени t.

Для фиксированного момента времени для двух сечений можно эаписать.

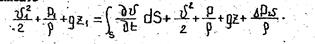
Сумма, представляющая механическую энергию в первом сечении, изменяется во времени. Поэтому и сумма вдоль канала тоже будет функцией времени.

Изменение механической энергии потока между первым и вторым произвольным сечением в данный момент

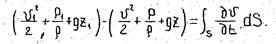
Значение интеграла представляет собой затрату механической энергии на преодоление инерции единицы массы жидкости находящейся между выбранными сечениями потока в данный интервал времени.

При течении вязкой жидкости разность значений механической энергии в рассматриваемых сечениях потока должна еще увеличиться и за счет гидравлических потерь.

Таким образом, при неустановившемся течении в трубе между двумя выбранными сечениями уравнение Бернулли будет иметь вид

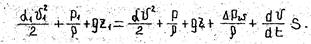
Это уравнение сохранения механической энергии, отнесенной к единице массы жидкости для неустановившегося течения.

Если механическую энергию отнести к единице веса жидкости, то оно приобретает следующий вед:

.

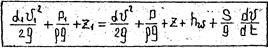17. Виды гидравлических сопротивлений (на трение, местные сопротивления, теоретическое обоснование расчета).

Потерянные на сопротивление напоры в зависимости от характера препятствий, делят на две большие группы:

- потери напора по длине потока, или потери напора на трение;

-потери напора за счет местных сопротивлений.

Потери напора на трение, или гидравлическое трение, обуславливаются вязкостью, реальных жидкостей и газов, возникающей при их движении, и являются результатом обмена количеством движения между молекулами (при ламинарном течении), а также и между отдельными частицами (при турбулентном движении) соседних слоев жидкости (газа), движущихся с различными скоростями.

Для преодоления сопротивления трения и поддержания равномерного поступательного движения жидкости необходимо, чтобы на жидкость действовала сила направленная в сторону её движения и равная силе сопротивления, т.е. на преодоление сопротивления трения нужно затрачивать энергию. Поэтому необходимую для преодоления сил сопротивления энергию или напор называют потерянной энергией или потерями напора.

При движении жидкости между нею и стенками трубы возникают дополнительные силы сопротивления, в результате чего частицы жидкости, прилегающие к поверхности трубы, тормозятся. Это торможение вследствие вязкости жидкости передается следующим слоям, причем скорость движения частиц по мере удаления от оси трубы постепенно уменьшается. Равнодействующая сил, сопротивления, Т, направлена в сторону противоположную движению, и параллельна направлению движения. Это и есть сила гидравлического трения (сопротивление гидравлического трения).

Потери напора за счет местных сопротивлений, возникают при местном нарушении нормального течения. За местные сопротивления принимают вентиль, кран, обратный клапан, внезапное расширение, сужение или поворот трубы, разветвление потока, протекание жидкости через отверстия, решетки, дроссельные устройства, обтекание различных препятствий и т.п. Эти явления усиливают обмен количеством движения между частицами движущейся .жидкости (т.е. трение), повышая потери энергии.

Таким образом, потери напора при движении жидкости складываются из потерь напора на трение и потерь напора на местные сопротивления, т.е.

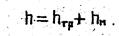
Потери напора на трение зависят от следующих факторов: диаметра трубы d и её длины L, физических свойств жидкости (плотности r и вязкости m), средней скорости движения жидкости в трубе V, средней высоты выступов шероховатости К на стенках трубы.

Формула для определения потерь на трение была получена в XIX в. эмпирическим путем и называется формулой Дарси - Вейсбаха:

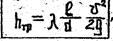
где l - коэффициент гидравлического трения, зависящий как от степени шероховатости стенок, так и от режима движения.

Потери напора на местное сопротивление находят по формуле Вейсбаха:

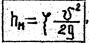
где V - коэффициент местных потерь; V - скорость потока после прохода через местное сопротивление.

Местные гидравлические сопротивления вызываются фасонными частями, арматурой и другим оборудованием трубопроводных сетей, которые изменяют величину или направление скорости движения жидкости на отдельных участках трубопровода (при расширении или сужении потока, в результате его поворота, при протекании потока, через диафрагмы, задвижки и т.д.), что всегда связано с появлением дополнительных потерь напора.

Потери напора, возникающие при преодолении какого-либо местного сопротивления, принято оценивать в долях скоростного напора, соответствующего скорости непосредственно за рассматриваемым местным сопротивлением, т.е. определять их по формуле Вейсбаха.

Коэффициенты разных местных сопротивлений находят, как правило, опытным путем. Таблицы значений этих коэффициентов (или формулы для них) содержатся в инженерных справочниках и руководствах по гидравлике. Для некоторых практически важных случаев значения коэффициентов местных сопротивлений удалось получить, также и теоретическим путем.

Иногда местные потери напора выражают в виде эквивалентной длины Lэ прямого участка трубопровода, сопротивление трения которого по величине равно рассматриваемым местным потерям напора т.е. из условия

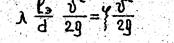
или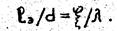

Таким образом, эквивалентная длина учитывает влияние коэффициента гидравлического трения трубопровода, где имеется местное сопротивление, на величину местных потерь напора. В соответствии с этой формулой V возрастает прямо пропорционально l, а следовательно, уменьшается с повышением числа Рейнольдса и снижением относительной шероховатости. При заданной геометрии местного сопротивления V является функцией коэффициента гидравлического трения l.

Основные виды местных потерь напора можно условно разделить на следующие группы:

- потери, связанные с изменением живого сечения потока ( или, что то же, его средней скорости), куда относятся случаи расширения и сужения потока (внезапного или постепенного);

-потери, вызванные изменением направления потока, его поворотом (движение жидкости в коленах, угольниках, отводах на трубопроводах);

-потери, связанные с протеканием жидкости через арматуру различного типа (вентили, краны, обратные клапаны, сетки, отборы, дроссель-клапаны и т.д.);

-потери, возникшие вследствие отделения одной части потока от другой или слияния двух потоков в один общий (движение жидкости в тройниках, крестовинах и отверстиях в боковых стенках трубопроводов при наличии транзитного расхода).

На участках многих местных сопротивлений скорости потока резко возрастают, в результате чего давление в нем уменьшается. Если давление становится ниже давления насыщенных паров жидкости, протекающей через местное сопротивление (или непосредственно за ним), возникает кавитация, неблагоприятно отражающаяся на работе оборудования и приводящая к вибрации, шумам и эрозионному разрушению материала. При наличии кавитации местные потери напора заметно возрастают. Кавитационные свойства местных сопротивлений оцениваются по критическому значению безразмерного числа – числа кавитации X, при котором в данном местном сопротивлении начинается кавитация:

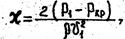
P1 – давление перед местным сопротивлением; Pкр - минимальное давление, при котором возникает кавитация, V1 - средняя скорость перед местным сопротивлением.

Обычно кавитация возникает при минимальном давлении, равном давлению насыщенных паров, т.е.

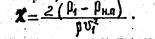
При достижении числом кавитации предельно допустимого (критического) значения Xкр в рассматриваемом местном сопротивлении начинается кавитация. Значения критического числа кавитации для разных местных сопротивлений определяются, как правило, экспериментально. Они связаны с коэффициентом местного сопротивления в бескавитационном режиме. В первом приближении для местных сопротивлений, вызванных изменением сечения потока, можно предложить зависимость:

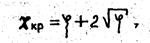
где V - коэффициент местного сопротивления.

Если известно значение критического числа кавитации Xкр, то предельно допустимую скорость в трубопроводе перед местным сопротивлением определяют по формуле:

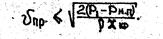
Для скоростей, не превышающих Vпр коэффициенты местного сопротивления определяют без учета влияния кавитации.

18. Режимы движения жидкости. Физический смысл критерия Рейнольдса, его практическое значение.

В природе существуют два различных вида движения жидкости: ламинарное (от латинского слова Lamina – слой, пластина) и турбулентное (от латинского слова turbulentus - вихревой). При ламинарном движении отдельные слои жидкости скользят относительно друг друга, не смешиваясь между собой. При турбулентном или неупорядоченном движении частицы жидкости движутся по сложным, все время изменяющимся траекториям, и в жидкости происходит интенсивное перемешивание.

Уже давно известно, что вязкие жидкости (масло) движутся большей частью упорядоченно, а маловязкие жидкости (вода, воздух) – почти всегда неупорядоченно. Ясность в вопросе о том, как именно будет происходить движение жидкости в тех или иных условиях, внесена в 1883 г. в результате опытов английского физика Рейнольдса.

Опыты Рейнольдса показали, что переход от ламинарного течения к турбулентному происходит при определенной скорости, возрастающей с увеличением, вязкости и снижающейся с уменьшением диаметра трубы. Рейнольдс установил, что состояние потока жидкости в трубе (режим) зависит от безразмерного числа, которое учитывает основные факторы, определяющие это движение: среднюю скорость V, диаметр трубы d, плотность жидкости r и её динамическую вязкость m

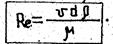
Диаметр d может быть заменен любым линейным размером, связанным с условиями течения или обтекания (диаметр плавающего в жидкости шара, обтекаемой жидкостью пластинки и др.).

Число Рейнольдса, при котором происходит переход от ламинарного движения к турбулентному, называют критическим и обозначают Reкр. При Re>Reкp режим является турбулентным, при Re<Reкр - ламинарным. Критическое число Рейнольдса зависит от условий входа в трубу, шероховатости её стенок, отсутствия или наличия первоначальных возмущений в жидкости, конвективных токов и др.

Наиболее часто в расчетах принимают для критического числа Рейнольдса, при движении жидкости в трубах, значение Reкр=2000, отвечающее переходу движения жидкости из турбулентного в ламинарное; при переходе движения из ламинарного в турбулентное критическое число Рейнольдса имеет большую величину.

Критическое число Rекр увеличивается в сужающихся трубах и уменьшается в расширяющихся. Это можно объяснить тем, что при ускорении .движения частиц жидкости в сужающихся трубах их тенденция к поперечному перемешиванию уменьшается, а при замедленном течении в расширяющихся трубах усиливается.

По критическому числу Reкр можно найти критическую скорость, ниже которой всегда будет происходить ламинарное движение:

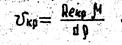
В трубопроводах систем отопления, водоснабжения, вентиляции, газоснабжения и др. движение, как правило, является турбулентным, так как движущаяся среда (вода, воздух, газ, пар) имеет малую вязкость. Ламинарный режим возможен лишь в трубах очень малого диаметра. Более вязкие жидкости, например масла, могут двигаться ламинарно даже в трубах большого диаметра.

С переходом .ламинарного движения в турбулентное изменяется характер распределения скоростей по сечению трубы, а также характер гидравлических сопротивлений.

При ламинарном движении распределение скоростей по сечению имеет параболический характер: непосредственно у стенок скорости равны нулю, а при удалении от них непрерывно и плавно возрастают, достигая максимума на оси трубы (рис. а). При турбулентном движении закон распределения скоростей сложнее; в большей части поперечного сечения скорости лишь незначительно меньше максимального значения (на оси), но зато вблизи стенок величина скорости резко падает в, пределах очень тонкого слоя называемого вязким или пристенным подслоем (рис. б).

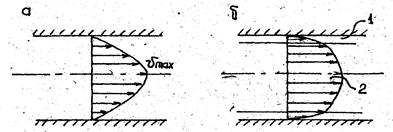
Рис. Распределение скоростей при ламинарном (а) и турбулентном (б) движении жидкости в трубах: I - вязкий подслой; 2 - ядро потока

Более равномерное распределение скоростей по сечению при турбулентном движении объясняется наличием турбулентного перемешивания, осуществляемого поперечными составляющими скоростей. Благодаря этому перемешиванию, частицы с большими скоростями в центре потока и с меньшими скоростями на его периферии, непрерывно сталкиваясь, выравнивают свои скорости. У самой стенки турбулентное перемешивание парализуется наличием твёрдых границ, поэтому там наблюдается значительно более быстрое падение скорости.

Измеряя разность уровней в двух пьезометрах, присоединенных к сечениям 1-1 и 2-2 трубы постоянного диаметра, можно определить потерю напора между этими сечениями из уравнения Бернулли

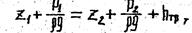
откуда

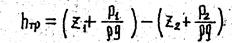
Таким образом, при равномерном движении уменьшение напора по длине трубы определяется разностью пьезометрических высот, отсчитываемых от одной и той же горизонтальной плоскости и, следовательно не зависит от расположения трубы в вертикальной плоскости.

Если пропускать воду по трубе с различной скоростью и, замерив при этом потери напора, построить кривую hтр=f(V), то она будет иметь вид представленный на рис.

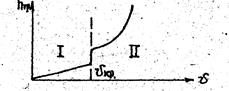
Рис. Зависимость потерь напора на трение от скорости движения жидкости

До Vкр, соответствующей переходу жидкости от ламинарного движения к турбулентному, потери напора изменяются прямо пропорционально скорости (зона I), затем вид кривой изменяется, и потеря напора становятся пропорциональными более высокой степени скорости (зона II).

Следовательно, ламинарный и турбулентный режимы отличаются не только характером движения частиц (наличием поперечных скоростей при турбулентном движении), но также особенностями распределения скоростей по сечению и характером зависимости между потерями напора и скоростью.

Ламинарное движение имеет слоистый характер и происходит без перемешивания частиц. Один слой движется по другому, причем между ними возникает сила трения.

Средняя скорость при ламинарном движении жидкости в трубе равна половине максимальной. Коэффициент Кориолиса a=2, то есть кинетическая энергия ламинарного потока вдвое больше кинетической энергии, подсчитанной по средней скорости.

Потери напора на трение при ламинарном режиме пропорциональны средней скорости движения и не зависят от состояния внутренней поверхности стенок трубы, т.к. характеристика состояния стенок не входит в формулу. Это можно объяснить тем, что жидкость прилипает к стенкам, в результате чего происходит трение жидкости о жидкость, а не жидкости о стенку.

Путем сопоставления формулы потерь напора на трение через гидравлический уклон, с общей зависимостью для потерь напора на трение, получим

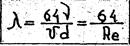
Отсюда следует, что при ламинарном режиме коэффициент гидравлического трения обратно пропорционален числу Рейнольдса.

При достижении числом Re критического значения на контактной поверхности потока с руслом непрерывно зарождаются турбулентные возмущения в виде вихрей различного размера и различной частоты. Эти вихри отрываются от стенок русла и пронизывают толщу поступательного потока, нарушая существовавшее до того упорядоченное (послойное) движение, характерное для ламинарного режима, вызывая в нем интенсивное турбулентное перемешивание. Диффузия образовавшихся у стенки вихрей сопровождается гашением содержащейся в них кинетической энергии турбулентности, при этом механическая энергия потока частично переходит в тепловую.

В результате исследований по сопротивлению трубопроводов были предложены различные эмпирические формулы для определения коэффициента гидравлического трения.

Для вполне шероховатых труб распространена формула

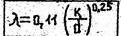
Для расчетов удобна формула Альтшуля, дающая зависимость l=f(Re,Kэ/d) в явном виде:

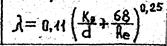
Т.к. l зависит от формы выступов, частоты, характера их расположения и т.д., то учесть влияние этих факторов непосредственно измерениями невозможно. В связи с этим в практику гидравлических расчетов было введено представление об эквивалентной равнозернистой шероховатости Кэ.

Под эквивалентной шероховатостью понимают такую высоту выступов шероховатости, сложенных из песчинок одинакового размера (шероховатость Никурадзе), которая дает при подсчетах одинаковый с заданной шероховатостью коэффициент гидравлического трения.

Таким образом эквивалентная шероховатость трубопроводов из различных материалов не определяется непосредственными измерениями высоты выступов, а находится при гидравлических испытаниях трубопроводов.

19. Основные задачи гидравлического расчета простого трубопровода.

При гидравлическом расчете трубопроводы подразделяют на простые и сложные. Простым называют трубопровод, состоящий из одной линии труб с постоянным расходом пути и передающий жидкость из резервуара в атмосферу или в другой резервуар. Сложные трубопроводы состоят из системы (сети) труб, подающей жидкость сразу в несколько точек. Сеть может быть разветвленной (разомкнутой или тупиковой), или кольцевой (замкнутой) и включать как транзитные (без раздачи жидкости по пути), так и распределительные трубопроводы.

Рассмотрим простой трубопровод, состоящий из труб одного и того же диаметра. При истечении в атмосферу уравнение Бернулли, записанное для сечений на поверхности воды в резервуаре и на выходе из трубы, имеет вид

Преобразовав, получим

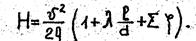(1)

При истечении под уровень аналогично получаем

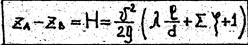(2)

Эти формулы тождественны между собой, и гидравлические расчеты для обеих схем трубопровода будут одинаковыми. Различие состоит только в том, что при истечении под уровень единица, стоящая в скобках в пpaвой части второго уравнения представляет собой коэффициент сопротивления “на выход” потока под уровень, в то время как при истечении в атмосферу она учитывает кинетическую энергию, ocтавшуюся в потоке после выхода из трубопровода, которая может быть так или иначе использована.

Таким образом, напор H при истечении под уровень равен сумме всех сопротивлений: H=Sh_w. При истечении же в атмосферу он делится на две части: кинетическую энергию, уносимую потоком из трубы, и сумму потерь напора

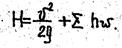
Гидравлический расчет простого трубопровода сводится к решению трех основных задач (для заданных конфигураций трубопровода, его материала и длины).

Первая задача. Требуется определить напор Н, необходимый для пропуска заданного расхода жидкости Q по заданному трубопроводу диаметром d и длиной l.

Задача решается путем непосредственного использования формулы (1) с предварительным вычислением средней скорости V=4Q/Пd².

Тогда искомый напор

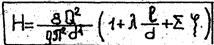(3)

Определение значений коэффициентов l и V в данной задаче не вызывает затруднений, так как число Рейнольдса заранее известно.

Вторая задача. Требуется определить пропускную способность (расход) трубопровода, Q при условии, что известны напор H, длина трубы l и её диаметр d.

Задача решается с помощью формулы (3), согласно которой

(4)

Так как коэффициенты l и V являются функциями числа Рейнольдса, которое связано с неизвестным и искомым здесь расходом Q, то решение находится методом попыток, полагая в первом приближении существование квадратичного закона сопротивления, при котором коэффициенты l и V не зависят от числа Рейнольдса.

Третья задача. Требуется определить диаметр трубопровода d при заданных расходах Q, длине трубопровода l и напоре H. Здесь Также используется формула (4), но возникают затруднения в вычислениях, так как не только неизвестно число Рейнольдса, но по отношению к искомому диаметру d мы получаем уравнение высших степеней или даже (при определении l по формуле Колбрука) трансцендентное уравнение. В связи с этим решаем задачу методом попыток, полагая в первом приближении наличие квадратичного закона сопротивления, при котором коэффициент l является функций только диаметра (при заданной шероховатости стенок трубы). Тогда уравнение (4) приводится к виду

Задаваясь рядом значений диаметра d1, d2, …,dn и вычисляя по формуле (4) соответственно ряд значений расхода Q1, Q2, …,Qn, строим график Q=f(d) (рис.), из которого определяем диаметр, отвечающий заданному расходу.

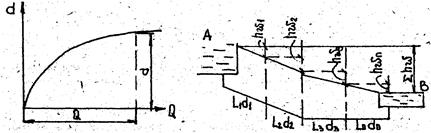
Рис. 1-К расчету диаметра при заданном расходе; 2-последовательное соединение трубопроводов.

Рассмотрим простой трубопровод, составленный из труб разного диаметра (рис.), уложенных в линию одна за другой (последовательное соединение труб). Уравнение Бернулли для этого случая можно записать в виде

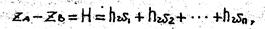
где hw1, hw2 - потери напора на первом, втором и т.д. участках трубопровода.

Потери напора на первом участке с диаметром трубы d1

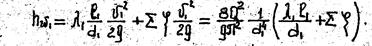
Аналогично для последующих участков

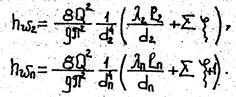
В последнем равенстве в скобках добавлено третье слагаемое - единица, учитывающая потери напора на выход.

Таким образом расчетное уравнение имеет вид

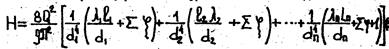(5)

Из уравнения (5) видно, что решение первой и второй задач будет таким же, как для трубопровода постоянного диаметра. Третья же задача, если в ней есть потребность определения всех диаметров для всех участков, становится неопределенной, так как в этом случае уравнение (5) содержало бы n неизвестных. Очевидно, что для определенности решения надо задавать диаметры труб для всех участков кроме одного.

20. Гидравлический расчет длинных трубопроводов в квадратичной области сопротивления.

В зависимости от соотношения между местными потерями напора и потерями на трение трубопроводы делятся на короткие и длинные. В длинных трубопроводах потери напора на трение во много раз превосходят потери на местные сопротивления (ll/d>>SV). Примерами длинных трубопроводов являются магистральные водопроводы, в которых местные потери напора часто составляют менее 2...3% потерь на трение и ими можно пренебречь. В коротких трубопроводах (всасывающие трубы насосных установок, трубы под насыпями; дюкеры и пр.) местные потери напора соизмеримы с потерями на трение.

Для длинных трубопроводов уравнения (1) и (2) можно записать в виде

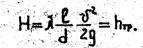(6)

Из уравнения (6) следует, что в длинных трубопроводах весь напор практически затрачивается на преодоление сопротивлений на трение по длине.

Уравнение (3) приводится к виду

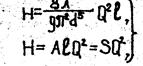(7)

а уравнение (4) к виду

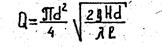
или

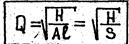(8)

где А - удельное сопротивление трубопровода,

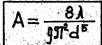
S – сопротивление трубопровода,

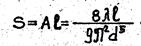
Если обозначить,

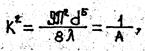
то уравнение (7) имеет вид

(12)

Показатель К, имеющий размерность расхода называется модулем расхода или расходной характеристикой труьопровода.

Показатели A, S и К преддтавляют собой обобщенные гидравлические параметры трубопровода, использование которых значительно упрощает гидравлические расчеты.

Рассмотрим случай, когда движение жидкости в трубопроводе происходит в условиях квадратичного закона сопротивлений. Здесь коэффициент гидравлического трения не зависит от числа Рейнольдса и является функцией только относительной шероховатости трубопровода, что значительно упрощает расчеты.

Действительно, для квадратичной области сопротивления параметры A и К зависят только от диаметра трубопровода (при заданной его шероховатости), а параметр S - от диаметра и длины трубопровода. Следовательно, значения обобщенных гидравлических параметров могут быть заранее вычислены для каждого диаметра d, входящего в установленный стандарт, и сведены в таблицы.

Три основных задачи по расчету трубопроводов с использованием обобщенных гидравлических параметров решаются следующим образом:

1) определение напора Н, необходимого для пропуска расхода Q по заданному трубопроводу диаметром d, производится непосредственно по формуле (7) или (12);

2) для определения пропускной способности трубы Q при заданных d,l,H предварительно находится из таблиц значение А (или K), после чего используется формула (8) или (12);

3) для определения необходимого диаметра d при заданных Q, l и Н предварительно из формул (7) или (12) находится значение A (или К), по которым из таблиц находим значение d.

При последовательном соединении трубопроводов различных диаметров и длины полная потеря напора в трубопроводе

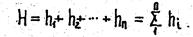
Подставляя для каждой потери напора её выражение по формуле (7) получим

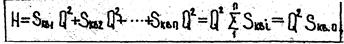(13)

где

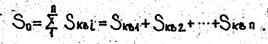
Таким образом при последовательном соединении трубопроводов сопротивления отдельных участков складываются.

Из уравнения (13) находим выражение для пропускаемого расхода:

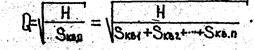
По найденному расходу можно вычислить потери напора на отдельных участках (например, h1=S1Q² и т.д.) и построить кривую давления .(пьезометрическую кривую), которая будет иметь вид ломаной линии .

Неквадратичная область сопротивления.

При движении жидкости в напорных трубопроводах санитарно-технических систем квадратичный закон сопротивления соблюдается не всегда. Так, например, более 80% всех городских газопроводов низкого и среднего давления работают в неквадратичной области сопротивления. В это случае параметры А (или К) зависят не только от диаметра трубы, но также и от скорости движения в ней, в связи с чем решение задач по гидравлическому расчёту трубопроводов несколько усложняется.

Формулу (7) можно представать в виде

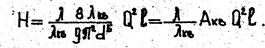(16)

Введем обозначение

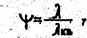
y - поправка на неквадуатичность

Тогда формула (16) примет вид

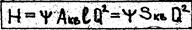
Определяем l по формуле Альтшуля и получим

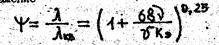(19)

Методика решения задач в неквадратичной области сопротивления.

Требуется определить пропускную способность трубопровода Q, если заданы напор H, длина трубы l и диаметр трубопровода d (вторая типовая задача).

По таблицам находим значение удельного сопротивления А при заданных d и К. Определяем пропускную способность трубопровода при квадратичном законе сопротивления.

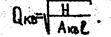
При скорости движения воды V по формуле (19) определяем значение поправки на неквадоатичность y, и вычисляем значения искомого расхода: Q=Qквy^0,5.

Если требуется определить диаметр трубопровода d при заданных Q,Н и l (третья типовая задача), то решение находим следующим образом.

Вычисляем значения удельного сопротивления (принимая y=1) по формуле А=H/(Q²l). По таблице находим для вычисленного значения соответствующий диаметр d1, пользуясь при этом линейной интерполяцией. Затем определяем скорость, соответствующую квадратичному сопротивлению (при диаметре d1).

По таблице или формуле (19), пользуясь найденной скоростью V, определяем поправку y, после чего вычисляем значение А по формуле (2-е приближение)

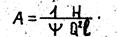
По таблице находим диаметр, отвечающий полученному значению А. Учитывая, что местные потери напора в неквадратичной области не меняются можно перенести предлагаемую методику и на короткие трубопроводы.

21. Уравнение расчета трубопроводов при последовательном соединении труб.