Модели распределения видового обилия

Разнообразие обычно анализируется с учетом четырех основных теоретических моделей:

геометрическое;

логарифмическое;

логарифмическинормальное (лог-нормальное);

распределение, описываемое моделью «разломанного стержня» Макартура.

Если изобразить каждую из моделей в виде графиков с осями ранг/обилие, можно увидеть переход от геометрического ряда к модели «разломанного стержня». При геометрическом распределении доминируют немногие виды при очень низкой численности большинства, при логарифмическом и лог-нормальном распределении виды со средним обилием становятся все более и более обычными; в распределении, описываемом моделью «разломанного стержня», обилия видов распределены с максимально возможной в природе равномерностью. Каждой из моделей соответствует характерная форма кривой на графике с осями ранг/обилие (рис. 5.3.1).

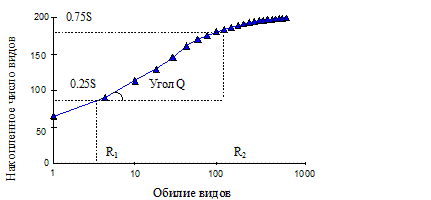Рис. 5.3.1. Кривые доминирования – разнообразия разных моделей видового обилия по Мэгарран (1992): 1 – геометрическое распределение; 2 – логарифмическое; 3 – лог-нормальное распределение; 4 – модель «разломанного стержня»

Геометрическое распределение выражается прямой линией с крутым наклоном. Логарифмическое распределение также имеет крутой наклон, но это не прямая линия, а кривая. Модель «разломанного стержня» имеет более пологий график. Лог-нормальное распределение описывается S-образной кривой, которая располагается на графике между логарифмическим распределением и моделью «разломанного стержня».

5.3.1. Геометрический ряд

Рассмотрим ситуацию, когда вид-доминант захватывает часть k некоего ограниченного ресурса, второй по обилию вид захватывает такую же долю k остатка этого ресурса, третий по обилию – k от остатка и т. д., пока ресурс не будет разделен между всеми S видами. Если это условие выполнено, и если обилия видов (выраженные, например, их биомассой или числом особей) пропорциональны используемой доле ресурса, распределение этих обилий будет описываться геометрическим рядом (или гипотезой преимущественного захвата ниши).

Пример такого ряда: наиболее обильный вид в два раза многочисленнее следующего за ним по обилию, а этот последний в свою очередь вдвое многочисленнее третьего и т. д. На графике ранг/обилие такое сообщество будет представлено прямой линией. Можно предположить, что в этом случае доминирующий вид занимает половину доступного пространства ниш, второй – половину оставшегося пространства (1/4 исходного) и т. д. Таким образом, каждый вид занимает прежде всего свободную нишу, не перекрывающуюся с другими.

Модель геометрического распределения была предложена Мотомурой. Модель имеет два параметра: n_i – численность самого обильного вида и k – константу геометрической прогрессии. В геометрическом ряду обилия видов от наибольшего к наименьшему выражаются формулой, разработанной Мэйем и Мотомурой:

,

где n_i – число особей i-го вида, N – общее число особей, – константа, при которой .

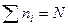Распределение обилий видов по типу геометрического обнаруживается преимущественно в бедных видами местообитаниях или в сообществах на очень ранних стадиях сукцессии. Такое распределение характерно для некоторых растительных сообществ в суровых условиях окружающей среды (например, сообщество растений субальпийского пояса).

5.3.2. Логарифмическое распределение

Модель логарифмического распределения известного английского математика Фишера была первой попыткой описать отношение между числом видов и числом особей этих видов. Особенным успехом эта модель пользовалась в энтомологических исследованиях и была впервые применена Фишером как теоретическая модель для описания распределения видов в коллекциях. Этой модели и статистике разнообразия было посвящено подробное исследование Л. Р. Тейлора с соавторами [Taylor et al., 1976].

Распределение частот видов для логарифмического распределения описывается следующей последовательностью:

,

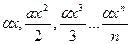где aх – число видов, представленных одной особью, aх²/2 – число видов, представленных двумя особями и т. д.

Логарифмическая модель имеет два параметра a и x. Это означает, что для выборки объемом N и числом видов S существует только одно возможное распределение частот видов по их относительному обилию, так как и a, и х являются функциями N и S. Чем больше выборка, извлеченная из данного сообщества, тем больше значение х и тем меньше доля особей, относящихся к видам, представленных одной особью в выборке. Два параметра S и N (общее число особей) связаны между собой зависимостью , где a – индекс разнообразия, который можно получить из уравнения:

,

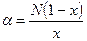где сумма всех особей N, принадлежащих S видам:

.

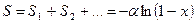Моделью логарифмического распределения, характеризующейся малым числом обильных видов и большой долей «редких», с наибольшей вероятностью можно описать такие сообщества, структура которых определяется одним или немногими экологическими факторами.

Как показали исследования, проведенные Мэгарран в Ирландии [1992], такому ряду соответствует распределение обилий видов растений наземного яруса в хвойных культурах в условиях низкой освещенности.