Логарифмическинормальное распределение

Для большинства сообществ характерно лог-нормальное распределение обилий видов, но обычно эта модель указывает на большое, зрелое и разнообразное сообщество. Такое распределение характерно для систем, когда величина некоей переменной определяется большим числом факторов.

Эта модель впервые была применена к распределению обилий видов Престоном. На разнообразном эмпирическом материале он показал, что частоты видов в больших выборках распределены в соответствии с логарифмическинормальным законом. По разработанной им методике в частотные классы группируются виды с числом особей, заключенным в промежутках, которые ограничены числами геометрической прогрессии. Престон нанес на ось обилия видов в масштабе логарифма по основанию 2 (log ₂) и назвал получившиеся классы октавами. Но для описания модели можно использовать любое основание логарифма. На графике распределения частот видов по полученным таким способом классам численности соответствуют известной кривой нормального распределения, усеченной слева, в области частот редких видов.

Распределение обычно записывается в форме:

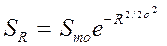, где

S_R – теоретическое число видов в октаве, расположенной в R октавах от модальной октавы; S_mo – число видов в модальной октаве; s – стандартное отклонение теоретической лог-нормальной кривой, выраженное в числе октав.

Рис. 5.3.2. Лог-нормальное распределение

Лог-нормальное распределение описывается симметричной «нормальной», т. е. колоколообразной кривой (рис. 5.3.2.). Однако если данные, которым она соответствует, получены из ограниченной выборки, то левая часть кривой (т. е. редкие, неучтенные виды) будет выражена нечетко. Престон назвал такую точку усечения кривой слева «линией занавеса». «Линия занавеса» может сдвигаться влево при увеличении объема выборки. На рисунке она указана стрелкой. Для большинства выборок выражена только часть кривой справа от моды. Только при огромном количестве данных, собранных на обширных биогеографических территориях, прослеживается полная кривая. S-образная кривая указывает на сложный характер дифференциации и перекрывания ниш. Большинство видов в природных открытых экосистемах существует в условиях соревнования за ресурсы, а не на условиях прямой конкуренции; множество адаптаций дает возможность делить ниши без конкурентного исключения из местообитания. Эта модель наиболее вероятна для ненарушенных сообществ.

5.3.4. Распределение по модели «разломанного стержня» Макартура

Эту модель иногда называют гипотезой случайной границы ниши. В 1975 году Макартур предложил три гипотетических распределения особей по видам в сообществе, основанных на различных типах взаимоотношений ниш разных видов:

1) ниши видов в сообществе не перекрываются, но тесно прилегают друг к другу;

2) ниши видов частично перекрываются;

3) ниши видов не перекрываются и разделены промежутками.

Наиболее подробно Макартур исследовал свойства первого гипотетического сообщества. Он сравнил разделение пространства ниши в пределах сообщества со случайным и одновременным разламыванием стержня на S кусков. S видов разделяют среду случайно между собой так, что они занимают неперекрывающиеся ниши. При этом число особей каждого вида пропорционально размеру (ширине) ниши. Эта модель рассматривает только один ресурс. Она отражает более равномерное его разделение, чем лог-нормальная модель, логарифмическая и геометрическая модели. Модель «разломанного стержня» характеризуется только одним параметром S (числом видов) и сильно зависит от объема выборки.

Число особей в i-ом по порядку обилия среди S видов (N_i) получают по формуле:

,

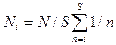где N – общее число особей, а S – общее число видов.

Эту модель можно выразить также в величинах стандартного распределения обилий видов согласно выражению, описанному Мэем:

.

Модель Макартура предполагает, что пространство ниш поделено на случайные, соприкасающиеся, но неперекрывающиеся участки. Такое распределение характерно для сообществ с интенсивной межвидовой конкуренцией, территориальным поведением, например, для лесных птиц, характер распределения которых соответствует представлению о неперекрывающихся случайных нишах. Лучше всего использовать модель «разломанного стержня» для доказательства большей выравненности обилий видов в определенном сообществе.