Мощность множества
1.Пусть заданы два конечных множества X и Y, причем N(X)= 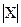 ; N(Y)=
; N(Y)= 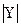 , тогда количество элементов в объединении двух множеств X и Y определяется по формуле
, тогда количество элементов в объединении двух множеств X и Y определяется по формуле 

 N(
N( 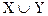 )=N(X)+N(Y)-N(
)=N(X)+N(Y)-N( 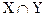 ).
).
В самом деле, N(X)+N(Y) есть число элементов, которые мы получим, перечисливвсе элементы множества X, а затем – все элементы множества Y. Но в этом случае общие элементы (их число равно 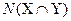 будут перечислены дважды, то есть
будут перечислены дважды, то есть 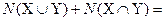 N(X)+N(Y), откуда и следует приведенная формула.
N(X)+N(Y), откуда и следует приведенная формула.
Справедлива следующая теорема: если 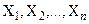 – произвольные множества, то
– произвольные множества, то
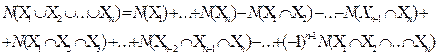
(Эта формула доказывается методом математической индукции).
Метод подсчета по данной формуле, состоящий в поочередном сложении и вычитании, называется методом включений и исключений.
2. Для любого разбиения конечного множества 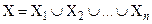 справедливо равенство
справедливо равенство
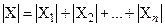 ,
,
которое называют правилом суммы.
3. Для любого покрытия конечного множества 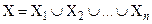 выполняется соотношение
выполняется соотношение
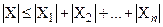 ,
,
которое называется обобщенным правилом суммы.
4. Для любых конечных множеств 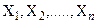 имеет место равенство
имеет место равенство
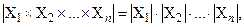
которое называется правилом произведения.
Если 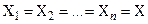 , то
, то 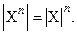
5. Если 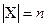 , то
, то 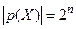 .
.
Дата добавления: 2015-04-10; просмотров: 1587;
