ЭЛЕМЕНТЫ ТЕОРИИ МНОЖЕСТВ
1.1. Основные понятия и определения теории множеств
Любое понятие дискретной математики можно определить с помощью понятия множества, которое является одним из фундаментальных понятий и было сформулировано впервые немецким математиком Г. Кантором.
Под множеством понимается любая совокупность определенных и различимых между собой объектов, мыслимая как единое целое.
Можно говорить о множестве стульев в комнате, людей, живущих в г. Воронеже, студентов в группе, о множестве натуральных чисел, букв в алфавите, состояний системы и т. п. При этом о множестве можно вести речь только тогда, когда элементы множества различимы между собой. Например, нельзя говорить о множестве капель в стакане воды, так как невозможно четко и ясно указать каждую отдельную каплю.
Отдельные объекты, из которых состоит множество, называют элементами множества. Так, число 3 – элемент множества натуральных чисел, а буква б – элемент множества букв русского алфавита.
Общим обозначением множества служит пара фигурных скобок { }, внутри которых перечисляются элементы множества. Для обозначения конкретных множеств используют различные прописные буквы A, S, X... или прописные буквы с индексами А1, А2. Для обозначения элементов множества в общем виде используют различные строчные буквы а, s, x... или строчные буквы с индексами а1, а2...
Для указания того, что некоторый элемент а является элементом множества S, используется символ Î принадлежности множеству. Запись aÎS означает, что элемент a принадлежит множеству S, а запись xÏS означает, что элемент х не принадлежит множеству S. Записью х1, x2,... ...,xnÎS пользуются в качестве сокращения для записи x1ÎS, x2ÎS,..., xnÎS.
Как правило, считается, что все элементы множества различны. Множество с повторяющимися элементами называется мультимножеством. Мультимножества играют важную роль в комбинаторике. В дальнейшем будут рассматриваться множества с различными элементами.
Будем использовать следующие обозначения для числовых множеств:
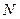 – множество натуральных чисел, т.е.
– множество натуральных чисел, т.е. 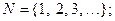
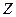 – множество целых чисел, т.е.
– множество целых чисел, т.е. 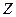 = {0, ±1, ±2, …};
= {0, ±1, ±2, …};
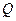 – множество рациональных чисел,
– множество рациональных чисел, 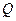 ={
={ 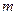 /
/ 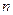 \
\ 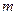 ,
, 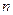 Î
Î 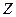 ;
; 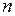 ¹ 0};
¹ 0};
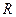 – множество вещественных чисел;
– множество вещественных чисел;
 – множество комплексных чисел.
– множество комплексных чисел.
Множества бывают конечными и бесконечными. Множество называют конечным, если число его элементов конечно, т. е. если существует натуральное число n, являющееся числом элементов множества. Множество называют бесконечным, если оно содержит бесконечное число элементов. Количество элементов конечного множества называется мощностью и обозначается 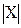 =n, если множество X содержит n элементов.
=n, если множество X содержит n элементов.
Важным понятием теории множеств является понятие пустого множества. Пустым множеством называют множество, не содержащее ни одного элемента. Пустое множествообозначают символом 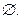 Например:
Например:
{xÎR | x2-x+1=0}= 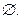
Понятие пустого множества играет очень важную роль при задании множеств с помощью описания. Так, без понятия пустого множества мы не могли бы говорить о множестве отличников группы или о множестве вещественных корней квадратного уравнения, не убедившись предварительно, есть ли вообще в данной группе отличники или имеет ли данное уравнение вещественные корни. Введение пустого множества позволяет совершенно спокойно оперировать с множеством отличников группы, не заботясь о том, есть или нет в рассматриваемой группе отличники. Пустое множество будем условно относить к конечным множествам.
Множество, содержащие все элементы, находящиеся в рассмотрении, называется универсальным или универсумом и обозначается U.
Для того чтобы оперировать с конкретными множествами, нужно уметь их задавать. Существуют два способа задания множеств: перечисление и описание. Задание множества способом перечисления соответствует перечислению всех элементов, составляющих множество. Так, множество отличников группы можно задать, перечислив студентов, которые учатся на отлично, например {Иванов, Петров, Сидоров}. Для сокращения записи Х={х1, х2, ...,хn} иногда вводят множество индексов I={1, 2,..., n} и пишут X={xi}, iÎI. Такой способ удобен при рассмотрении конечных множеств, содержащих небольшое число элементов, но иногда он может применяться и для задания бесконечных множеств, например {2, 4, 6, 8...}. Естественно, что такая запись применима, если вполне ясно, что понимается под многоточием.
Описательный способ задания множества состоит в том, что указывается характерное свойство, которым обладают все элементы множества. При этом используется запись
X={x | x обладает свойством Q(x)}.
Выражение в скобках читается: множество всех элементов х, которые обладают свойством Q(x). Так, если М — множество студентов группы, то множество A отличников этой группы запишется в виде А={хÎМ | х – отличник группы},
что читается следующим образом: множество А состоит из элементов х множества М, обладающих тем свойством, что х является отличником группы.
В тех случаях, когда не вызывает сомнений, из какого множества берутся элементы х, указание о принадлежности х множеству М можно не делать. При этом множество А запишется в виде
А={х | х – отличник группы}.
Приведем несколько примеров задания множеств методом описания: {x | x – четное} – множество четных чисел;
{х | х2–1=0} – множество {+1, –1}.
Пусть Z – множество целых чисел. Тогда {xÎZ | 0<x£7} есть множество {1, 2, 3, 4, 5, 6, 7}.
Множество нечетных чисел можно определить как {x | x=2k+1 для некоторого kÎZ}.
Способ задания множества с помощью свойств таит некоторые опасности, поскольку «неправильно» заданные свойства могут привести к противоречию. Приведем один из наиболее типичных парадоксов – парадокс Рассела. Рассмотрим множество всех множеств, которые не являются своими собственными элементами: 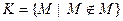 . Спросим теперь, является ли множества К своим элементом? Если КÎК, то должно выполняться свойство, задающее множество К, т.е. КÏК, что приводит к противоречию. Если КÏК, то, поскольку выполняется свойство, задающее К, приходим к тому, что КÎК, а это противоречит предположению. Таким образом, не всякое свойство приводит к осмысленному заданию множества.
. Спросим теперь, является ли множества К своим элементом? Если КÎК, то должно выполняться свойство, задающее множество К, т.е. КÏК, что приводит к противоречию. Если КÏК, то, поскольку выполняется свойство, задающее К, приходим к тому, что КÎК, а это противоречит предположению. Таким образом, не всякое свойство приводит к осмысленному заданию множества.
Кроме того, множество можно задать с помощью характеристической функции, значения которой указывают является ли (да или нет) х элементом множества Х :
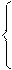
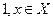
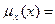
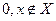
Заметим, что для любых элементов 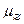 = 0;
= 0;  = 1.
= 1.
Пример. Пусть на универсуме U={a,b,c,d,e} определено множество X={a,c,d}, тогда
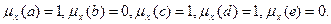
Для произвольных множеств X и Y можно определить два типа отношений – отношение равенства и отношение включения.
Два множества считаются равными, если они состоят из одних и тех же элементов. Принято обозначение X=Y, если X и Y равны, и X 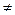 Y – иначе.
Y – иначе.
Легко видеть, что для любых множеств X, Y, Z справедливы соотношения
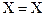 ,
,
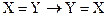 ,
,
( 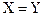 и
и  )
) 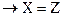 .
.
Из определения равенства множеств вытекает, что порядок элементов в множестве несуществен. Так, например, множества {3, 4, 5, 6} и {4, 5, 6, 3} представляют собой одно и то же множество.
Если каждый элемент множества X является элементом множества Y, то говорят, что X включено в Y и обозначают 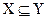 :
:
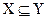
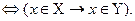
В этом случае говорят, что множество X является подмножеством множества Y. В частности X и Y могут совпадать, поэтому 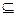 называется также отношением нестрогого включения. Отметим некоторые свойства подмножества, вытекающее из его определения:
называется также отношением нестрогого включения. Отметим некоторые свойства подмножества, вытекающее из его определения:
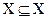 ,
,
( 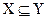 и
и 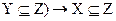 .
.
Если 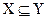 и
и 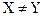 , то говорят, что X есть собственное подмножество Y и обозначают
, то говорят, что X есть собственное подмножество Y и обозначают 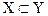 , отношение между множествами в этом случае называется отношением нестрогого включения. Для отношения строгого включения справедливо
, отношение между множествами в этом случае называется отношением нестрогого включения. Для отношения строгого включения справедливо
( 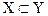 и
и 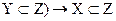 .
.
Невключение подмножества X в множество Y обозначается 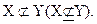
Пример. Пусть Y — множество студентов группы, а Х – множество отличников той же группы. Так как каждый отличник группы является в то же время студентом этой группы, то множество X является подмножеством множества Y.
Замечание. Не следует смешивать отношение принадлежности Î и отношение включения 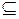 . Хотя
. Хотя 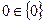 и
и 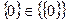 , неверно, что
, неверно, что 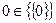 , поскольку единственным элементом множества
, поскольку единственным элементом множества 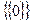 является {0}.
является {0}.
Пример. Справедливы следующие включения: NÌZ, ZÌQ, QÌR, RÌC.
Заметим, что если X является подмножеством Y и наоборот, то X и Y состоят из одних и тех же элементов, поэтому
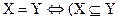 и
и 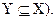
Таким образом, чтобы доказать равенство двух множеств, надо установить два включения.
Пример. Покажем, что множества М1={x | sin x = 1} и M2={x | x = 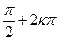 ,
, 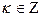 } совпадают.
} совпадают.
Если x 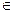 М1, то x является решением уравнения sin x=1. Но это значит, что x можно представить в виде x=
М1, то x является решением уравнения sin x=1. Но это значит, что x можно представить в виде x= 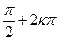 и поэтому x
и поэтому x 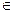 М2. Таким образом,
М2. Таким образом, 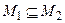 . Если x
. Если x 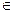 М2, т.е. x=
М2, т.е. x= 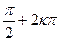 , то sin x=1, т.е.
, то sin x=1, т.е. 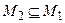 . Следовательно, М1=М2.
. Следовательно, М1=М2.
Для каждого множества X существует множество, элементами которого являются различные подмножества множества X. Такое множество называется семейством множества или булеаном множества X и обозначается P(X) Так как 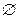 включено в любое множество, то
включено в любое множество, то 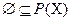 .
.
Пример. Пусть 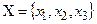 . Тогда
. Тогда
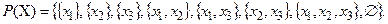
Дата добавления: 2015-04-10; просмотров: 2763;
