Древовидная организация данных
Древовидной организацией данных (деревом) называется множество записей, расположенных по уровням следующим образом:
- на 1-м уровне расположена только одна запись (корень дерева),
- к любой записи i-го уровня ведет адрес связи только от одной записи уровня i-1.
Количество уровней в дереве называется рангом. Записи дерева, которые адресуются от общей записи (i-l)-ro уровня, образуют группу. Максимальное число элементов в группе называется порядком дерева. Деревья обычно формируются двунаправленными, адрес связи от записи уровня i+1 к записи i-го уровня называется обратным.
При размещении дерева в памяти ЭВМ каждая запись может занимать произвольное место.
Рассмотрим деревья порядка 2 (бинарные). Они интересны тем, что составляющие их записи могут быть упорядочены. Для этого один из атрибутов записи должен быть объявлен ключевым.
Запись А - корень дерева. Записи, у которых заполнены два адреса связи, называются полными, записи с одним заполненным адресом - неполными, записи с двумя незаполненными адресами - концевыми. На рис. 7 записи А, В, Е, F - полные, С - неполная, D, H, I, J, G -концевые. Адреса связи делятся на левые и правые. Так, адрес от Е к G -левый, от Е к Н - правый. Каждая запись имеет левую и правую ветви. Правую (левую) ветвь записи образует поддерево, адресованное из этой записи через правый (левый) адрес связи. У записи С правая ветвь состоит из записей F, I, J, левая ветвь пустая.
В упорядоченном бинарном дереве значение ключевого атрибута каждой записи должно быть больше, чем значение ключа у любой записи на ее левой ветви, и не меньше, чем ключ любой записи на ее правой ветви. Это определение позволяет также различать левые и правые адреса (ветви).
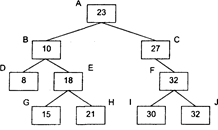
Рисунок 3.5. Пример бинарного дерева
а)Упорядоченное бинарное дерево формируется из неупорядоченного массива записей по специальному алгоритму. Этот алгоритм создает дерево из первой записи массива, затем -дерево из первых двух записей, из первых трех записей и так далее до исчерпания всех записей массива.
Алгоритм формирования упорядоченного бинарного дерева:
1) Первая запись массива с ключом р(1) становится корнем дерева.
2) Значение ключа второй записи р(2) сравнивается с р(1), находящимся в корне дерева. Если р(2)<р(1), то вторая запись помещается на левой от корня ветви, в противном случае - на правой ветви. Сейчас получено упорядоченное дерево из первых двух записей, далее на каждом шаге создается упорядоченное дерево из первых i записей.
3) Для i-й записи массива ключ p(i) сравнивается с корневым значением, и выполняется переход по левому адресу если p(l)>p(i)), а при p(l)<=p(i) - по правому адресу. Ключ достигнутой записи также сравнивается с p(i), и снова организуется переход по левому или правому адресу и т. д. Когда будет достигнут незаполненный адрес связи, то он должен адресовать запись с ключом p(i). Указанные действия повторяются до исчерпания всех записей исходного массива.
б) В процессе поискаданных по совпадению в упорядоченном бинарном дереве просматривается некоторый путь по дереву, начинающийся всегда в его корне. Искомое значение ключа q сравнивается со значением корня р(1). Если p(l)>q, просмотр дерева продолжается по левой ветви корня, если p(l)<=q - по правой.
Поиск заканчивается, когда у какой-либо записи отсутствует адрес связи, необходимый для дальнейшего продолжения поиска. Количество сравнений С пропорционально logM
в) Включение новой записи при корректировке упорядоченного бинарного дерева означает выполнение одного шага алгоритма формирования дерева с включаемой записью на входе.
Сложность исключения зависит от того, какая запись исключается - концевая, неполная или полная. Первые два случая аналогичны корректировке при списковой организации данных. Адрес связи на исключаемую концевую запись заменяется на признак конца строки, адрес связи на исключаемую неполную запись заменяется на ее собственный адрес связи.
При исключении полной записи решается задача о подстановке на ее место другой записи, такой, что ее ключ не нарушает общей упорядоченности бинарного дерева - такие записи называются соседними. Соседняя слева запись - это запись с ключом, который непосредственно меньше ключа данной записи, а ключ соседней справа записи равен или непосредственно больше, чем ключ данной записи.
Дата добавления: 2015-03-09; просмотров: 959;
