ИССЛЕДОВАНИЕ ДИЭЛЕКТРИЧЕСКИХ ПОТЕРЬ

(доц. Мельников Ю.П., доц. Шувалов В.В.)

Как показал Г. Лоренц, использование классических представлений о строении вещества достаточно для качественного понимания многих оптических явлений. В частности, это относится и к дисперсии света, т.е. к зависимости показателя преломления вещества от длины волны излучения.

При прохождении через вещество световой волны на каждый электрон, входящий в частицы вещества (молекулы или атома) действует дополнительная сила электрической природы

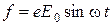. (1)

На основании второго закона Ньютона можно получить уравнение вынужденных колебаний электрона:

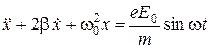, (2)

где т – масса электрона; 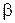– коэффициент затухания колебаний; 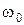– частота собственных колебаний электрона в молекуле (атоме).

Решение уравнения (2) состоит из суммы общего решения однородного уравнения ( 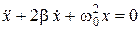), которое запишется

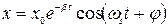, (3)

где 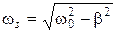, и частного решения неоднородного уравнения (2):

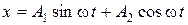. (4)

Общее решение однородного уравнения дает значения, затухающие за время 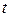, которое очень мало. Таким образом, стационарное решение уравнения (2) должно включать только незатухающие частные решения (4). Подставляя частное решение (4) в уравнение (2) получим тождество:

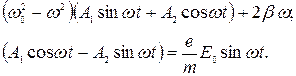(5)

Это тождество должно удовлетворяться в любой момент времени, поэтому должны быть равны отдельно коэффициенты пр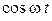и и 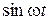в левой и правой частях тождества (5). Отсюда получим систему уравнений для А₁ и А₂:

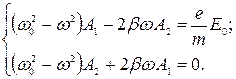(6)

Решаем эту систему, например, подставляя решения для А₂ из второго уравнения в первое, получим выражения для А₁ и А₂:

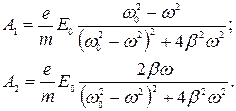(7)

Представим частное решение неоднородного уравнения (4) с помощью комплексных амплитуд, т.е. считаем, что 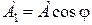и 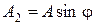. Тогда частное решение уравнения (2) можно записать в виде

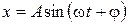, (8)

где 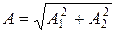– суммарная амплитуда, а 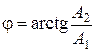– дополнительная фаза, возникающая при наличии затухания.

Для А и 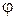, используя формулы (7), получим:

.

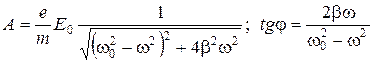Из решения (8) с учетом формулы для А и 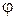(9) и уравнения колебаний (2) видно, что при больших временах 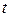амплитуда вынужденных колебаний сильно зависит от разности 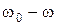, а фаза колебаний зависит от знака разности ( 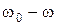) и может быть такова, что электрон будет колебаться в противофазе с вынуждающей силой электромагнитной волны, что будет при 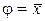. Так как смещение электронов приводит к поляризации диэлектрика, то от фазы колебания электронов зависит и поляризация диэлектрика.

Далее для упрощения вычислений положим 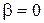, при этом изменение фазы колебания вблизи резонансной частоты 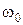будет создаваться изменением знака амплитуды А. Получим:

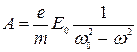. (10)

Электрон под действием падающей волны будет совершать колебательное движение:

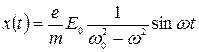. (11)

В результате смещения электрона происходит разделение зарядов в молекуле и возникает единичный дипольный момент:

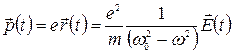, (12)

где 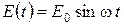– электрическое поле электромагнитной волны. Далее считаем, что .

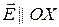Вектор поляризации вещества - это дипольный момент единицы объема вещества, который можно вычислить, умножив единичный дипольный момент на количество смещающихся электронов в единице объема:

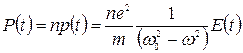. (13)

Отсюда диэлектрическая проницаемость вещества равна:

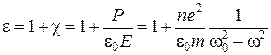; (14)

Учитывая связь между 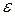и показателем преломления п, 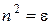, получим:

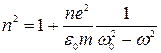. (15)

Через длину волны 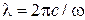это выражение для п² можно записать в виде:

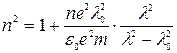. (16)

Во второе слагаемое формулы (15), входит множитель размерности 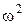, который дает важную характеристику вещества:

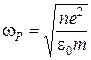, (17)

которая называется плазменной или ленгмюровской частотой. Эта частота связана с собственными коллективными колебаниями электронов в веществе.

Так удивительным образом оказывается, что величина, характеризующая коллективные движения электронов в плазме попадает в уравнение (16), выражающее зависимость показателя преломления от длины волны, хотя мы рассматривали колебательные движения электронов в атомах вещества. Этот результат можно объяснить тем, что колебания плазмы аналогичны поляризации диэлектрика.

Теперь вернемся к формуле (16). Можно показать, что зависимость 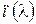в области нормальной дисперсии (длина волны излучения 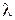достаточно далеко от характеристической длины волны, введенной по определению 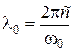) может быть приближенно выражена формулой:

.

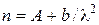Наша работа ставит своей целью подтвердить этот вывод теории и следует сказать, что аккуратно поставленный эксперимент дает возможность это сделать.

ИССЛЕДОВАНИЕ ДИЭЛЕКТРИЧЕСКИХ ПОТЕРЬ

Цель работы: изучение диэлектрических свойств структуры Ta – Ta₂O₅ – металл в радиочастотном диапазоне.