Середні величини.
Середні величини – це узагальнююча міра ознаки, що варіює, у статистичній сукупності, тобто це узагальнюючий показник, який характеризує типовий рівень ознаки , що варіює, в розрахунку на одиницю сукупності.
Середня величина - узагальнюючий показник. Який характеризує сукупність однотипних явищ за змінною кількісною ознакою. Середня величина показує типове, характерне значення ознаки, віднесене до одиниць статистичної сукупності.
Умови наукового використання середніх величин:
- якісна однорідність сукупності;
- сукупність має бути достатньо великою;
- використання загальних середніх з груповими.
Призначення середніх в економічному аналізі:
- характеристика рівня масових суспільних явищ;
- проведення порівняльного аналізу;
- вивчення тенденцій розвитку явищ;
- вибіркове спостереження;
- вимірювання взаємозв’язків.
В статистиці використовують різні види середніх величин. Застосування того чи іншого виду середньої залежить від виду ряду розподілу. Змісту ознаки і мети використання. Критерієм правильного вибору виду середньої величини є запис логічної формули розрахунку.
Статистика розглядає наступні види середніх величин:
- середня арифметична,
- середня гармонійна,
- середня геометрична,
- середня квадратична
Кожна з цих середніх може розраховуватися як для не згрупованих даних – проста середня, так і для згрупованих даних – зважена середня.
- середня хронологічна,
- порядкові середні (мода, медіана, квартилі, децилі).
Розрахункові формули, мету застосування і критерій застосування того чи іншого виду середньої величини подамо у таблиці.
| Вид середньої | Критерій вибору виду | Розрахункова формула | Інша інформація | |
| простої | зваженої | |||
Середня арифметична 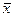
| Є однією з найбільш поширених середніх. Її використовують для характеристики рядів розподілу, сума окремих значень ознаки в яких утворює загальний обсяг ознаки. Інакше, використовується за первинними не згрупованими (проста) або згрупованими (зважена) даними коли, відповідно, відомо і чисельник і знаменник логічної формули, не відомо чисельник а відомо знаменник . Логічна формула : середня = загальний обсяг ознаки/загальний обсяг сукупності | 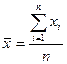
| 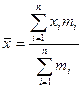
| Для визначення середньої в інтервальному варіаційному ряді необхідно попередньо визначити серединні ( центральні0 значення варіант як середину інтервалу , переходячи до дискретного ряду і застосувати середню зважену. Якщо при цьому початковий інтервал є відкритим, то його довжина відповідає довжині наступного інтервалу, і якщо відкритим є останній інтервал, то довжина його відповідає довжини попереднього інтервалу.
Властивості.
- Середня сталої величини дорівнює цій сталій:
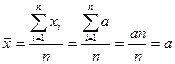 - Якщо кожну з варіант ряду розподілу збільшити ( зменшити) на певну сталу величину А. то і середня зміниться на цю величину:
- Якщо кожну з варіант ряду розподілу збільшити ( зменшити) на певну сталу величину А. то і середня зміниться на цю величину:
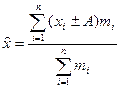 , ,
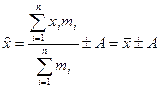 -Якщо кожну з варіант ряду розподілу помножити (розділити) на певну сталу величину А, то і середня зміниться на цю величину:
-Якщо кожну з варіант ряду розподілу помножити (розділити) на певну сталу величину А, то і середня зміниться на цю величину:
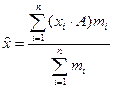
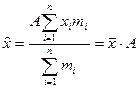 -Якщо усі частоти помножити (розділити) на певну сталу величину, то середня від цього не зміниться:
-Якщо усі частоти помножити (розділити) на певну сталу величину, то середня від цього не зміниться:
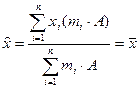 - Сума відхилень варіант від середньої дорівнює нулю:
- Сума відхилень варіант від середньої дорівнює нулю:
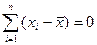 - сума квадратів відхилень значень варіант від середньої є меншою за суму квадратів відхилень від будь-якої іншої величини6
- сума квадратів відхилень значень варіант від середньої є меншою за суму квадратів відхилень від будь-якої іншої величини6
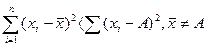 З урахуванням цих властивостей обчислення середньої арифметичної для інтервального варіаційного ряду з рівними інтервалами можна виконати методом моментів першого порядку за такою формулою:
З урахуванням цих властивостей обчислення середньої арифметичної для інтервального варіаційного ряду з рівними інтервалами можна виконати методом моментів першого порядку за такою формулою:
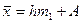
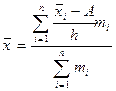 , ,
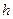 -довжина інтервалу, А- «умовний нуль» або центральне значення ознаки з найвищою частотою, -довжина інтервалу, А- «умовний нуль» або центральне значення ознаки з найвищою частотою, 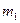 - момент першого порядку, - момент першого порядку, 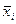 - центральне значення ознаки у відповідному інтервалі. - центральне значення ознаки у відповідному інтервалі.
|
Середня гармонійна 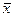
| Є величиною, яка обернена до середньої арифметичної. Має складнішу конструкцію і використовується у випадках, коли за частоти береться добутки значень варіант ознаки на їх чисельність( 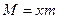 . Середня гармонійна вживається тоді, коли не задано обсягу сукупності а задано обсяг значень ознаки( варіанти . Середня гармонійна вживається тоді, коли не задано обсягу сукупності а задано обсяг значень ознаки( варіанти 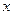 зважуються за значеннями зважуються за значеннями 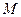 ). Інакше. Середня гармонійна використовується за не згрупованими та згрупованими даними коли в логічній формулі середньої відомо чисельник а невідомо знаменник ). Інакше. Середня гармонійна використовується за не згрупованими та згрупованими даними коли в логічній формулі середньої відомо чисельник а невідомо знаменник
| 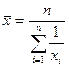
| 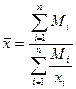
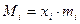 - обсяг значень ознаки - обсяг значень ознаки
| |
Середня геометрична 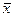
| Використовується, якщо визначальна властивість сукупності (обсяг значень ознаки) формується як добуток індивідуальних значень ознаки. Найбільш широко використовується при аналізі рядів динаміки з метою визначення середніх коефіцієнтів (темпів) зміни рівнів ряду. | 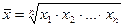 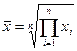
| 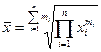
| |
Середня квадратична 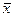
| Використовується при визначенні абсолютних і відносних показників варіації. Середня квадратична використовується у випадку сумування квадратів значень варіант | 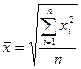
| 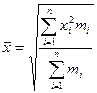
| |
Середня хронологічна 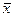
| Використовується у рядах динаміки при визначенні середнього рівня моментного ряду. Якщо у хронологічному ряду наведено моментні показники, то для обчислення середньої вони замінюються пів сумами значень на початок і кінець періоду. Якщо моментів більш ніж два і інтервали між ними рівні. То середня обчислюється за середньою хронологічною. | 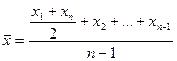
| ||
| Порядкові середні | Використовуються при визначенні характеристик рядів розподілу і форм розподілу | Дискретний ряд розподілу | Інтервальний ряд розподілу | |
Мода 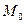
| Значення варіанти, яке найчастіше зустрічається в ряді розподілу.( Найбільш поширене значення ознаки, домінанта0 | В ряді розподілу знайти максимальну частоту 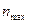 і значення варіанти, яке відповідає цій частоті і буде модою і значення варіанти, яке відповідає цій частоті і буде модою 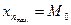
| В ряді розподілу знайти модальний інтервал, інтервал з максимальною частотою. У цьому інтервалі моду знайти за формулою:
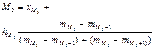
| |
Медіана 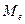
| Значення варіанти, яке припадає на середину впорядкованого ряду розподілу, поділяє його навпіл – на дві рівні за обсягом частини | Визначають використовуючи кумулятивні частоти 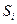 . Серед всіх кумулятивних частот знаходять таку, яка не менша за половину обсягу сукупності тобто таку, що . Серед всіх кумулятивних частот знаходять таку, яка не менша за половину обсягу сукупності тобто таку, що 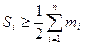 . Варіанта, яка відповідатиме їй і буде медіаною. . Варіанта, яка відповідатиме їй і буде медіаною.
| Визначаютьмедіанний інтервал як інтервал з кумулятивною частотою не меншою за половину обсягу сукупності. В медіанному інтервалі медіану шукають за формулою
 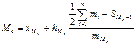
| |
Квартилі
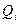
| Значення варіант , які поділяють сукупність на чотири рівні за обсягом частини. Є три . Другий дорівнює медіані. | Визначають використовуючи кумулятивні частоти 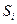 . Серед всіх кумулятивних частот знаходять таку, яка не менша за j/4 обсягу сукупності тобто таку, що . Серед всіх кумулятивних частот знаходять таку, яка не менша за j/4 обсягу сукупності тобто таку, що 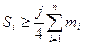 . .
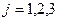 Варіанта, яка відповідатиме їй і буде відповідним квартелем.
.
Варіанта, яка відповідатиме їй і буде відповідним квартелем.
.
| Визначаютьквартильний інтервал як інтервал з кумулятивною частотою не меншою за j/4 обсягу сукупності. В інтервалі квартилі шукають за формулою
 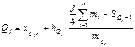
| |
Децилі
| Значення варіант , які поділяють сукупність на десять рівних за обсягом частини Є дев'ять. П'ятий дорівнює медіані | Аналогічно до медіани і квартилів | Аналогічно до медіани і квартилів |
Дата добавления: 2015-03-07; просмотров: 1717;
