Характеристики центра розподілу.
Характеристиками центру розподілу в будь-якому ряді розподілу є:
| Характеристика | Зміст | Визначення |
Центр розподілу
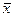
| Типовий рівень ознаки, узагальнююча характеристика всього розмаїття її індивідуальних значень. Розраховується у формі середньої величини – середня арифметична зважена . | 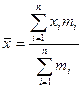
|
Мода ( домінанта)
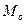
| Найбільш поширене значення групувальної ознаки у статистичній сукупності. Значення ознаки, яке найчастіше зустрічається в сукупності. | Дискретний ряд. В ряді розподілу знайти максимальну частоту 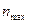 і значення варіанти, яке відповідає цій частоті і буде модою і значення варіанти, яке відповідає цій частоті і буде модою 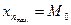
|
Інтервальний ряд.
В ряді розподілу знайти модальний інтервал, інтервал з максимальною частотою. У цьому інтервалі моду знайти за формулою:
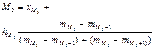
| ||
Медіана
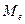
| Значення ознаки, що припадає на середину впорядкованого ряду. Іншими словами, це значення ознаки, яка поділяє ряд розподілу на дві рівні за обсягом частини | Дискретний ряд
Визначають використовуючи кумулятивні частоти 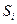 . Серед всіх кумулятивних частот знаходять таку, яка не менша за половину обсягу сукупності тобто таку, що . Серед всіх кумулятивних частот знаходять таку, яка не менша за половину обсягу сукупності тобто таку, що 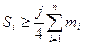 . .
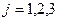 Варіанта, яка відповідатиме їй і буде медіаною.
Варіанта, яка відповідатиме їй і буде медіаною.
|
Інтервальний ряд.
Визначаютьмедіанний інтервал як інтервал з кумулятивною частотою не меншою за половину обсягу сукупності. В медіанному інтервалі медіану шукають за формулою
 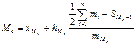
| ||
Квартилі
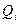
| Значення варіант , які поділяють сукупність на чотири рівні за обсягом частини. Є три . Другий дорівнює медіані. |
Дискретний ряд.
Визначають використовуючи кумулятивні частоти 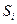 . Серед всіх кумулятивних частот знаходять таку, яка не менша за j/4 обсягу сукупності тобто таку, що . Серед всіх кумулятивних частот знаходять таку, яка не менша за j/4 обсягу сукупності тобто таку, що 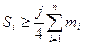 . .
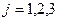 Варіанта, яка відповідатиме їй і буде відповідним квартелем..
Варіанта, яка відповідатиме їй і буде відповідним квартелем..
|
Інтервальний ряд
Визначаютьквартильний інтервал як інтервал з кумулятивною частотою не меншою за j/4 обсягу сукупності. В інтервалі квартилі шукають за формулою
 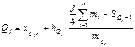
| ||
Децилі
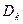
| Значення варіант , які поділяють сукупність на десять рівних за обсягом частини Є дев'ять. П'ятий дорівнює медіані | Дискретний ряд.
Визначають використовуючи кумулятивні частоти 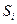 . Серед всіх кумулятивних частот знаходять таку, яка не менша за j/10 обсягу сукупності тобто таку, що . Серед всіх кумулятивних частот знаходять таку, яка не менша за j/10 обсягу сукупності тобто таку, що 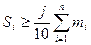 . .
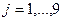 Варіанта, яка відповідатиме їй і буде відповідним децилем.
Варіанта, яка відповідатиме їй і буде відповідним децилем.
|
Інтервальний ряд
Визначаютьдецильний інтервал як інтервал з кумулятивною частотою не меншою за j/10 обсягу сукупності. В інтервалі децилі шукають за формулою
 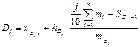
|
Дата добавления: 2015-03-07; просмотров: 839;
