Закономірності розподілу.

Будь-яка статистична сукупність формується під впливом певних причин і умов. Вони, з одного боку є типовими і спільними для всіх елементів статистичної сукупності, з іншого – випадковими та індивідуальними для кожного елементу. Ці умови та причини взаємопов’язані між собою. Так, взаємодія спільних і індивідуальних причин та умов визначає як індивідуальні значення ознак одиниць сукупності, так і розподіл останніх у межах сукупності. Характерні властивості сукупності відображаються в рядах розподілу.

Ряд розподілу – впорядкований розподіл одиниць сукупності на групи за певною ознакою, яка змінюється.

Елементи рядів розподілу:

1. Варіанта – значення ознаки за якою здійснюється групування - .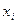

2. Частота – кількість повторень варіанти в сукупності -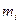

У рядах розподілу частоти варіант можуть задаватися в наступних формах:

1. У формі абсолютної величини – абсолютна частота 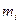- кількість повторень варіанти в сукупності.

2. У формі відносної величини – відносна частота – частка - 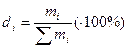- частка абсолютних частот варіант ряду розподілу у загальному обсязі сукупності.

3. Кумулятивна частота ( частка) - 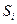- результат послідовного об'єднання груп і підсумування відповідних їм частот – нагромадження послідовне абсолютних (відносних) частот: .

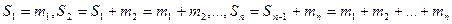Ряди розподілу в залежності від способу подання варіант поділяють на:

1. Атрибутивні – ряди, утворені за якісною ознакою поданою словесно.

2. Варіаційні – ряди, утворені за кількісними ознаками:

- дискретні – ознака є неперервна послідовність кількісних значень;

- інтервальні – ознака є відкритим. Закритим. Рівним та нерівним інтервалом.

Саме у співвідношенні варіант і частот в рядах розподілу і виявляється закономірність розподілу. Базою аналізу закономірностей розподілу є варіаційні дискретні ряди та варіаційні інтервальні ряди з рівними інтервалами.

Поглиблений аналіз закономірностей розподілу передбачає характеристику деяких особливостей статистичних сукупностей, зокрема:

- визначення типового рівня ознаки, який є центром розподілу;

- вимірювання варіації ознаки, тобто ступеня згрупованості індивідуальних значень ознаки навколо центру розподілу;

- оцінювання особливостей варіації. Тобто ступеня відхилення від симетрії;

- оцінювання нерівномірності розподілу значень ознаки між окремими елементами сукупності, тобто ступінь її концентрації.