Метрики связности по методам

Д. Биемен и Б. Кенг предложили метрики связности класса, которые основаны на прямых и косвенных соединениях между парами методов [15]. Если существуют общие экземплярные переменные (одна или несколько), используемые в паре методов, то говорят, что эти методы соединены прямо. Пара методов может быть соединена косвенно, через другие прямо соединенные методы.

На рис. 14.2 представлены отношения между элементами класса Stack. Прямоугольниками обозначены методы класса, а овалами — экземплярные переменные. Связи показывают отношения использования между методами и переменными.

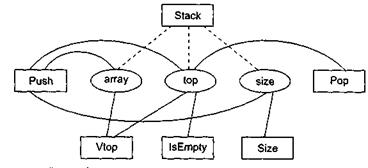
Рис. 14. 2. Отношения между элементами класса Stack

Из рисунка видно, что экземплярная переменная top используется методами Stack, Push, Pop, Vtop и IsEmpty. Таким образом, все эти методы попарно прямо соединены. Напротив, методы Size и Pop соединены косвенно: Size соединен прямо с Push, который, в свою очередь, прямо соединен с Pop. Метод Stack является конструктором класса, то есть функцией инициализации. Обычно конструктору доступны все экземплярные переменные класса, он использует эти переменные совместно со всеми другими методами. Следовательно, конструкторы создают соединения и между такими методами, которые никак не связаны друг с другом. Поэтому ни конструкторы, ни деструкторы здесь не учитываются. Связи между конструктором и экземплярными переменными на рис. 14.2 показаны пунктирными линиями.

Для формализации модели вводятся понятия абстрактного метода и абстрактного класса.

Абстрактный метод АМ(М) — это представление реального метода М ввиде множества экземплярных переменных, которые прямо или косвенно используются методом.

Экземплярная переменная прямо используется методом М, если она появляется в методе как лексема данных. Экземплярная переменная может быть определена в том же классе, что и М, или же в родительском классе этого класса. Множество экземплярных переменных, прямо используемых методом М, обозначим как DU(M).

Экземплярная переменная косвенно используется методом М, если: 1) экземплярная переменная прямо используется другим методом М', который вызывается (прямо или косвенно) из метода М; 2) экземплярная переменная, прямо используемая методом М', находится в том же объекте, что и М.

Множество экземплярных переменных, косвенно используемых методом М, обозначим как IU(М).

Количественно абстрактный метод формируется по выражению:

AM (М) = DU (М) 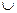IU (М).

Абстрактный класс АС(С) — это представление реального класса С в виде совокупности абстрактных методов, причем каждый абстрактный метод соответствует видимому методу класса С. Количественно абстрактный класс формируется по выражению:

АС (С) = [[AM (M) | M 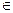V (С)]],

где V(C) — множество всех видимых методов в классе С и в классах — предках для С.

Отметим, что АМ-представления различных методов могут совпадать, поэтому в АС могут быть дублированные элементы. В силу этого АС записывается в форме мультимножества (двойные квадратные скобки рассматриваются как его обозначение).

Локальный абстрактный класс LAC(C) — это совокупность абстрактных методов, где каждый абстрактный метод соответствует видимому методу, определенному только внутри класса С. Количественно абстрактный класс формируется по выражению:

LAC(C)=[[AM(M)|M 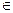LV(C)]],

где LV(C) — множество всех видимых методов, определенных в классе С.

Абстрактный класс для стека, приведенного в табл. 14.2, имеет вид:

AC (Stack) = [[{top}, {size}, {array, top}, {array, top, size}, {pop}]].

Поскольку класс Stack не имеет суперкласса, то справедливо:

AC (Stack) = LAC (Stack)

Пусть NP(C) — общее количество пар абстрактных методов в AC(C). NP определяет максимально возможное количество прямых или косвенных соединений в классе. Если в классе С имеются N методов, тогда NP(C) = N*(N- l)/2. Обозначим:

q NDC(C) — количество прямых соединений AC(Q;

q NIC(C) — количество косвенных соединений в АС(С).

Тогда метрики связности класса можно представить в следующем виде:

q сильная связность класса (Tight Class Cohesion (ТСС)) определяется относительным количеством прямо соединенных методов:

ТСС (С) = NDC (С) / NP (С);

q слабая связность класса (Loose Class Cohesion (LCC)) определяется относительным количеством прямо или косвенно соединенных методов:

LCC (С) = (NDC (С) + NIC (С)) / NP (С).

Очевидно, что всегда справедливо следующее неравенство:

LCC(C)>=TCC(C).

Для класса Stack метрики связности имеют следующие значения:

TCC(Stack)=7/10=0,7

LCC(Stack)=10/10=l

Метрика ТСС показывает, что 70% видимых методов класса Stack соединены прямо, а метрика LCC показывает, что все видимые методы класса Stack соединены прямо или косвенно.

Метрики ТСС и LCC индицируют степень связанности между видимыми методами класса. Видимые методы либо определены в классе, либо унаследованы им. Конечно, очень полезны метрики связности для видимых методов, которые определены только внутри класса — ведь здесь исключается влияние связности суперкласса. Очевидно, что метрики локальной связности класса определяются на основе локального абстрактного класса. Отметим, что для локальной связности экземплярные переменные и вызываемые методы могут включать унаследованные переменные.