Пример расчета коленчатого вала
Условие задачи[13]
Идеализированная расчетная схема коленчатого вала представлена на рис. 5.32. Левый и правый концы вала имеют шарнирное закрепление в вертикальной и горизонтальной плоскостях, перпендикулярных оси стержня. Правый конец, кроме того, жестко закреплен от продольного перемещения и поворота сечения вокруг оси стержня. Требуется подобрать радиус круглого сечения шатунной шейки (горизонтальная участок вала длиной 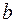 ) и размеры прямоугольного сечения кривошипа (вертикальные участки вала длиной
) и размеры прямоугольного сечения кривошипа (вертикальные участки вала длиной 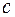 ) так, чтобы удовлетворялись условия статической и усталостной прочности вала. Примем следующие исходные данные:
) так, чтобы удовлетворялись условия статической и усталостной прочности вала. Примем следующие исходные данные: 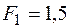 кН,
кН, 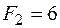 кН,
кН, 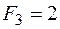 кН,
кН, 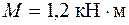 ,
, 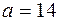 см,
см, 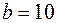 см,
см, 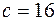 см,
см, 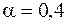 . Для кривошипа отношение сторон прямоугольного сечения
. Для кривошипа отношение сторон прямоугольного сечения 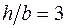 . Материал вала – сталь С275 с допускаемым напряжением 190 МПа. Пределы выносливости для симметричного цикла примем в соответствии с [4]: при изгибе
. Материал вала – сталь С275 с допускаемым напряжением 190 МПа. Пределы выносливости для симметричного цикла примем в соответствии с [4]: при изгибе 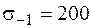 МПа, при кручении
МПа, при кручении 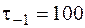 МПа.
МПа.
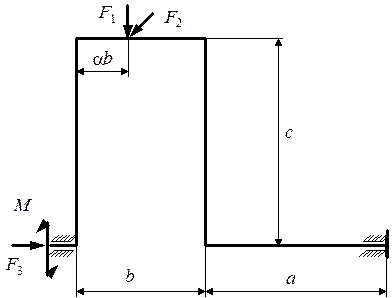 Рис. 5.32. Расчетная схема коленчатого вала
Рис. 5.32. Расчетная схема коленчатого вала
|
Решение
Определение внутренних усилий. Прежде всего надо найти внутренние усилия в сечениях вала, т. е. построить эпюры усилий. Для этого сначала определим опорные реакции. В заданных закреплениях на концах вала возникает шесть опорных реакций, показанных на рис. 5.33. Составим шесть уравнений статики:
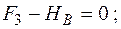
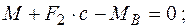
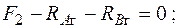
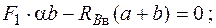
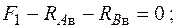
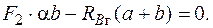
Из них получим 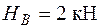 ;
; 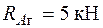 ;
; 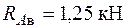 ;
; 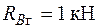 ;
; 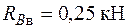 ;
; 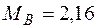 кН·м.
кН·м.
 Рис. 5.33. Местные системы координат для определения внутренних
усилий в расчетных сечениях 1–10
Рис. 5.33. Местные системы координат для определения внутренних
усилий в расчетных сечениях 1–10
|
При вычислении внутренних усилий используем местные системы координатных осей для каждого участка стержня. Направление оси 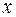 , совпадающей с осью стержня, следует сохранять на всех участках рамы. На рис. 5.33 оно соответствует обходу вдоль оси стержня слева направо. Оси
, совпадающей с осью стержня, следует сохранять на всех участках рамы. На рис. 5.33 оно соответствует обходу вдоль оси стержня слева направо. Оси 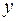 и
и 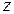 – главные центральные оси инерции поперечного сечения. Ось
– главные центральные оси инерции поперечного сечения. Ось 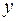 будем всегда направлять перпендикулярно плоскости чертежа, ось
будем всегда направлять перпендикулярно плоскости чертежа, ось 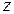 лежит в плоскости рисунка и меняет свое направление при переходе с одного участка рамы на другой (см. рис. 5.33). При определении усилий используем правила знаков для внутренних усилий, описанные во вступительной части гл. 5 и поясняемые рис. 5.1. Тогда, используя метод сечений, найдем внутренние усилия в расчетных сечениях 1–10:
лежит в плоскости рисунка и меняет свое направление при переходе с одного участка рамы на другой (см. рис. 5.33). При определении усилий используем правила знаков для внутренних усилий, описанные во вступительной части гл. 5 и поясняемые рис. 5.1. Тогда, используя метод сечений, найдем внутренние усилия в расчетных сечениях 1–10:
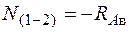 ;
; 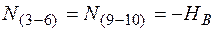 ;
; 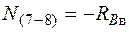 ;
;
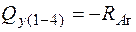 ;
; 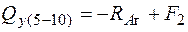 ;
;
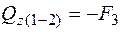 ;
; 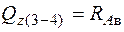 ;
; 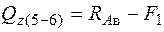 ;
;
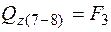 ;
; 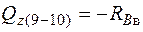 ;
;
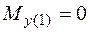 ;
; 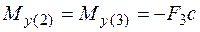 ;
;
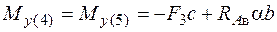 ;
;
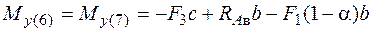 ;
;
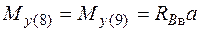 ;
; 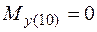 ;
;
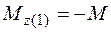 ;
; 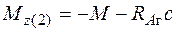 ;
; 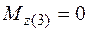 ;
;
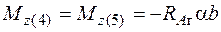 ;
; 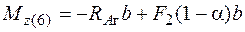 ;
;
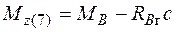 ;
; 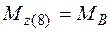 ;
;
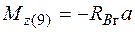 ;
; 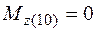 ;
;
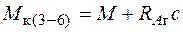 ;
; 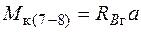 ;
; 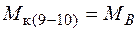 .
.
Эпюры внутренних усилий, построенные по принятым в условии задачи исходным данным, показаны на рис. 5.34. Эпюры изгибающих моментов откладываем со стороны растянутых волокон. Обратим внимание на соблюдение дифференциальных зависимостей между 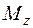 и
и 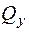 , а также между
, а также между 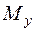 и
и 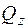 .
.
Предварительный подбор сечений шатунной шейки и кривошипа. После построения эпюр можно подобрать размеры поперечных сечений. Предварительный подбор сечений производим из условия статической прочности без учета напряжений от продольной и поперечных сил, а для прямоугольного сечения, кроме того, не учитываем напряжения от крутящего момента. При предварительном подборе сечения допускаемое напряжение примем пониженным – 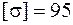 МПа, имея в виду снижение прочности металла за счет усталости при циклически меняющихся напряжениях и необходимости удовлетворения еще условию усталостной прочности. Сначала определим радиус круглого сечения шатунной шейки. Выберем опасное сечение, сравнив величины суммарных изгибающих моментов в потенциально опасных сечениях 3, 4–5 и 6 (см. рис. 5.33). Суммарный изгибающий момент находится по формуле
МПа, имея в виду снижение прочности металла за счет усталости при циклически меняющихся напряжениях и необходимости удовлетворения еще условию усталостной прочности. Сначала определим радиус круглого сечения шатунной шейки. Выберем опасное сечение, сравнив величины суммарных изгибающих моментов в потенциально опасных сечениях 3, 4–5 и 6 (см. рис. 5.33). Суммарный изгибающий момент находится по формуле
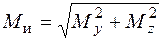 .
.
 Рис. 5.34. Эпюры внутренних усилий
Рис. 5.34. Эпюры внутренних усилий
|
В сечении 3 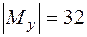 кН·см,
кН·см, 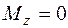 , тогда
, тогда 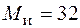 кН·см; в сечении 4(5)
кН·см; в сечении 4(5) 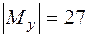 кН·см,
кН·см, 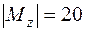 кН·см и
кН·см и 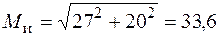 кН·см; наконец, в сечении 6
кН·см; наконец, в сечении 6 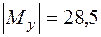 кН·см,
кН·см, 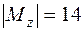 кН·см и
кН·см и 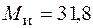 кН·см.
кН·см.
Видно, что опасным будет сечение 4(5), в котором действует суммарный момент 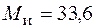 кН·см. Условие статической прочности в опасной точке этого сечения, полученное из третьей теории прочности, имеет вид (5.37)
кН·см. Условие статической прочности в опасной точке этого сечения, полученное из третьей теории прочности, имеет вид (5.37)
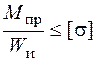 ,
,
где 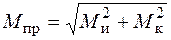 – приведенный момент, а
– приведенный момент, а 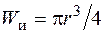 – момент сопротивления изгибу. Из условия статической прочности найдем необходимый радиус сечения шатунной шейки. В рассматриваемом примере
– момент сопротивления изгибу. Из условия статической прочности найдем необходимый радиус сечения шатунной шейки. В рассматриваемом примере
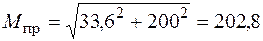 кН·см.
кН·см.
Из условия 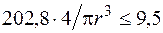 кН/см2 получим
кН/см2 получим 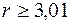 см. Так как в использованном условии прочности не учтена продольная сила, немного увеличим сечение. Достаточно округлить полученный размер в большую сторону. Примем
см. Так как в использованном условии прочности не учтена продольная сила, немного увеличим сечение. Достаточно округлить полученный размер в большую сторону. Примем 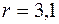 см.
см.
Теперь предварительно подберем размеры прямоугольного сечения кривошипа из условия прочности в угловых точках сечения, где действуют только максимальные нормальные напряжения от изгиба, а касательные напряжения равны нулю. Условие прочности в этих точках имеет вид (5.50).
Прежде чем находить размеры сечения, подумаем, как рационально расположить сечение. Поскольку в рассматриваемом примере 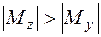 , то для обеспечения рациональной работы кривошипа сечение надо развернуть так, чтобы наибольшая сторона
, то для обеспечения рациональной работы кривошипа сечение надо развернуть так, чтобы наибольшая сторона 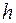 была расположена вдоль оси
была расположена вдоль оси 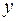 . Тогда
. Тогда 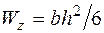 ,
, 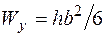 и
и 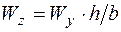 . Условие прочности (5.50) в этом случае запишется так:
. Условие прочности (5.50) в этом случае запишется так:
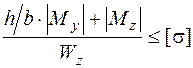 .
.
Чтобы выбрать опасное сечение, надо сравнить значение числителя в условии прочности в потенциально опасных сечениях правого[14] кривошипа (сечения 7, 8 на рис. 5.33). При 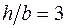 самым опасным сечением будет сечение 7, в котором
самым опасным сечением будет сечение 7, в котором 
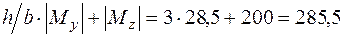 кН·см. Из условия прочности, считая допускаемое напряжение равным 95 МПа, найдем размер сечения кривошипа:
кН·см. Из условия прочности, считая допускаемое напряжение равным 95 МПа, найдем размер сечения кривошипа:
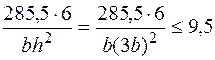 кН/см2.
кН/см2.
Отсюда 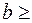 2,72 см. Округляя размер в большую сторону примем
2,72 см. Округляя размер в большую сторону примем 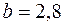 см,
см, 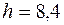 см.
см.
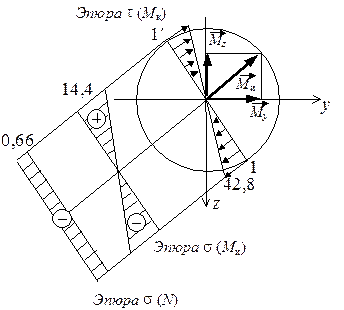 Рис. 5.35. Эпюры напряжений (в МПа) в опасном сечении шатунной шейки
Рис. 5.35. Эпюры напряжений (в МПа) в опасном сечении шатунной шейки
|
Построение эпюр напряжений. Построим эпюры напряжений в опасных сечениях с тем, чтобы найти положение дополнительных опасных точек и завершить в дальнейшем окончательную проверку статической прочности. Чтобы найти точное положение опасных точек в круглом сечении шатунной шейки, определим направление суммарного изгибающего момента. Изобразим пары 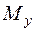 и
и 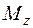 в виде векторов с учетом их знаков (в опасном сечении
в виде векторов с учетом их знаков (в опасном сечении 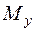 и
и 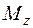 в соответствии с эпюрами отрицательны), определяя их направление по правилу правого винта (см. рис. 5.25). Нейтральная линия для круглого сечения перпендикулярна плоскости изгиба и совпадает с линией действия вектора полного изгибающего момента
в соответствии с эпюрами отрицательны), определяя их направление по правилу правого винта (см. рис. 5.25). Нейтральная линия для круглого сечения перпендикулярна плоскости изгиба и совпадает с линией действия вектора полного изгибающего момента 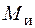 . На рис. 5.35 построены эпюры нормальных напряжений, вызванных действием изгибающего момента
. На рис. 5.35 построены эпюры нормальных напряжений, вызванных действием изгибающего момента 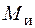 , продольной силы N, и эпюра касательных напряжений от крутящего момента
, продольной силы N, и эпюра касательных напряжений от крутящего момента 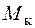 . На эпюрах напряжений учтены знаки усилий. Максимальные напряжения от продольной силы, изгиба и кручения найдены по формулам соответственно (5.33), (5.34) и (5.35).
. На эпюрах напряжений учтены знаки усилий. Максимальные напряжения от продольной силы, изгиба и кручения найдены по формулам соответственно (5.33), (5.34) и (5.35).
Построим эпюры распределения напряжений в прямоугольном сечении кривошипа (рис. 5.36). При определении максимальных нормальных напряжений, вызванных продольной силой и изгибающими моментами, использованы формулы (5.33), (5.44) и (5.45). Максимальные касательные напряжения от крутящего момента и поперечных сил найдены по формулам (5.46)–(5.49). Знаки нормальных напряжений соответствуют знакам усилий 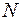 ,
, 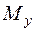 и
и 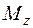 . Стрелками показаны направления касательных напряжений, вызванных усилиями
. Стрелками показаны направления касательных напряжений, вызванных усилиями 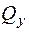 ,
, 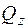 и
и  с учетом их знаков.
с учетом их знаков.
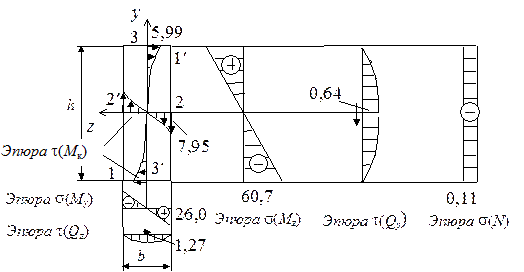 Рис. 5.36. Эпюры напряжений (в МПа) в опасном
сечении кривошипа
Рис. 5.36. Эпюры напряжений (в МПа) в опасном
сечении кривошипа
|
Проверка усталостной прочности шатунной шейки. Нормальные напряжения от изгиба изменяются по симметричному циклу, а нормальные напряжения от продольной силы постоянны, поэтому характеристики цикла, по которому меняются полные нормальные напряжения,
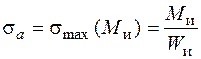 ,
, 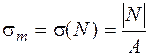 .
.
Касательные напряжения от кручения изменяются по пульсирующему (отнулевому) циклу с такими характеристиками:
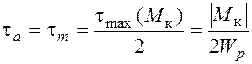 .
.
Найдем эти характеристики, считая радиус шатунной шейки равным 3,1 см. Тогда
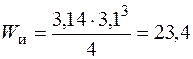 см3;
см3; 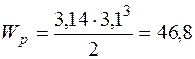 см3;
см3; 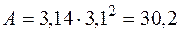 см2
см2
и
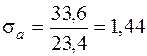 кН/см2;
кН/см2; 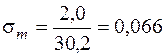 кН/см2;
кН/см2;
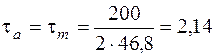 кН/см2.
кН/см2.
Сосчитаем коэффициенты запаса по формулам  (5.53), (5.54), (5.52). Примем следующие значения эмпирических коэффициентов:
(5.53), (5.54), (5.52). Примем следующие значения эмпирических коэффициентов:
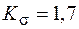 ;
; 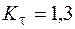 ;
; 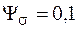 ;
; 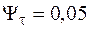 ;
; 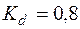 ;
; 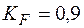 .
.
Тогда
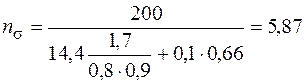 ;
;
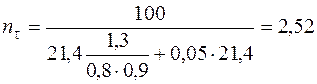 ;
;
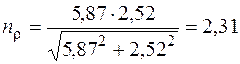 > 1,5,
> 1,5,
то есть условие усталостной прочности шатунной шейки выполняется.
Проверка статической прочности шатунной шейки и кривошипа. Проверка статической прочности производится на кратковременное двукратное увеличение нагрузки с учетом напряжений от всех внутренних усилий. Допускаемое напряжение при этом принимается равным 190 МПа.
По построенным ранее эпюрам напряжений выбираем опасные точки. Для круглого сечения шатунной шейки опасными могут быть точки 1, 1¢ (см. рис. 5.35). Для пластичного материала опасной является только точка 1, в которой нормальные напряжения от изгиба и продольной силы имеют один знак (в рассматриваемом примере знак "минус"). В этой точке, кроме того, действуют максимальные касательные напряжения, вызванные кручением. Таким образом, точка 1 находится в "балочном" напряженном состоянии. Проверку прочности в этой точке необходимо осуществлять по теориям прочности, соответствующим материалу. При подборе сечения в условии прочности точки 1 не учитывалась продольная сила. Теперь учтем ее влияние. В соответствии с условием окончательной проверки прочности увеличим найденные ранее напряжения в 2 раза. Сложим нормальные напряжения от изгиба и продольной силы в точке 1:
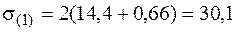 МПа.
МПа.
Касательные напряжения в точке 1 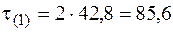 МПа. Подставим их в условие прочности по третьей теории (5.31):
МПа. Подставим их в условие прочности по третьей теории (5.31):
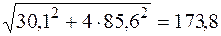 МПа < 190 МПа.
МПа < 190 МПа.
Таким образом, условие прочности в точке 1 шатунной шейки выполняется. то есть найденный радиус поперечного сечения 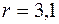 см, удовлетворяющий условию и статической, и усталостной прочности, является окончательным.
см, удовлетворяющий условию и статической, и усталостной прочности, является окончательным.
Для прямоугольного сечения кривошипа опасными могут быть три группы точек, показанных на рис. 5.36. В рассматриваемом примере будем проверять прочность в точках 1 (здесь нормальные напряжения от 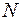 ,
, 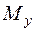 и
и 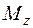 имеют один знак), 2 и 3 (в них складываются имеющие одинаковые направления касательные напряжения от крутящего момента и поперечных сил). Увеличим показанные на рис. 5.36 напряжения в 2 раза и проверим прочность в каждой из опасных точек:
имеют один знак), 2 и 3 (в них складываются имеющие одинаковые направления касательные напряжения от крутящего момента и поперечных сил). Увеличим показанные на рис. 5.36 напряжения в 2 раза и проверим прочность в каждой из опасных точек:
· В угловой точке 1 действуют максимальные по модулю нормальные напряжения, равные сумме напряжений от 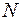 ,
, 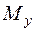 и
и 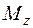 . Точка находится в линейном напряженном состоянии и условие прочности в этой точке
. Точка находится в линейном напряженном состоянии и условие прочности в этой точке
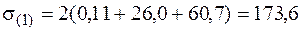 МПа < 190 МПа
МПа < 190 МПа
выполняется.
· В точке 2 по середине длинной стороны прямоугольника действуют и нормальные
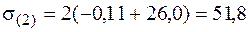 МПа,
МПа,
и касательные напряжения
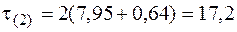 МПа.
МПа.
Точка находится в "балочном" напряженном состоянии и проверку прочности производим по третьей теории прочности (5.31):
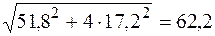 МПа < 190 МПа.
МПа < 190 МПа.
· Точка 3 по середине короткой стороны прямоугольника тоже находится в "балочном" напряженном состоянии. В ней действуют нормальные и касательные напряжения:
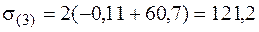 МПа;
МПа;
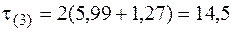 МПа.
МПа.
Условие прочности в этой точке по третьей теории прочности
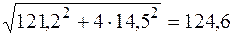 МПа < 190 МПа.
МПа < 190 МПа.
Поскольку условия прочности во всех опасных точках выполняются, окончательные размеры поперечного сечения кривошипа 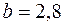 см;
см; 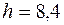 см.
см.
Дата добавления: 2015-03-07; просмотров: 1518;
