Основные определения. Коленчатый вал является плоской рамой, испытывающей действие пространственных циклических нагрузок, в которой возможно усталостное разрушение
Коленчатый вал является плоской рамой, испытывающей действие пространственных циклических нагрузок, в которой возможно усталостное разрушение, поэтому, кроме расчета на статические нагрузки, требуется учет влияния на напряжения динамического действия нагрузок. Известно, что под действием длительных, циклически меняющихся нагрузок материалы конструкций обнаруживают значительное понижение прочности. Это явление носит название усталости материала. Способность материала сопротивляться усталостному разрушению называют выносливостью. Важной характеристикой материала является предел выносливости, определяемый экспериментально. Следует отметить, что расчет на циклические нагрузки (усталостную прочность) носит эмпирический характер, требует наличия большого количества экспериментальных данных, обычно приводимых в справочниках в виде таблиц и графиков. Используемый в рассматриваемой задаче расчет на усталостную прочность является достаточно приближенным, так как многие необходимые для расчета величины эмпирических коэффициентов принимаются условно. Более точный расчет коленчатых валов рассматривается в специальных курсах.
Один из способов расчета на усталостную прочность сводится к определению действительного коэффициента запаса усталостной прочности 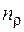 и сравнению его с нормируемым коэффициентом запаса n. В данном расчете примем
и сравнению его с нормируемым коэффициентом запаса n. В данном расчете примем 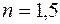 . Условием усталостной прочности является условие
. Условием усталостной прочности является условие
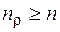 . (5.51)
. (5.51)
Для "балочного" напряженного состояния, которое имеет место в опасных точках коленчатого вала, коэффициент запаса усталостной прочности находится по формуле Гафа и Полларда
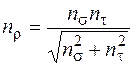 , (5.52)
, (5.52)
где 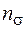 – запас прочности по нормальным напряжениям в предположении, что касательные напряжения равны нулю;
– запас прочности по нормальным напряжениям в предположении, что касательные напряжения равны нулю; 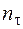 – запас прочности по касательным напряжениям, когда
– запас прочности по касательным напряжениям, когда 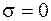 . Коэффициенты
. Коэффициенты 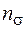 и
и 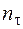 определяются следующим образом:
определяются следующим образом:
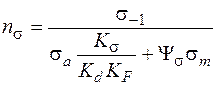 ; (5.53)
; (5.53)
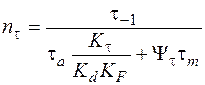 . (5.54)
. (5.54)
В формулах (5.53), (5.54) 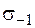 и
и 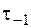 – пределы выносливости при изгибе и кручении для симметричного цикла;
– пределы выносливости при изгибе и кручении для симметричного цикла; 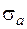 ,
, 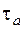 – амплитудные значения цикла напряжений при изгибе и кручении;
– амплитудные значения цикла напряжений при изгибе и кручении; 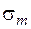 ,
, 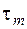 – средние напряжения цикла при изгибе и кручении. Остальные величины, входящие в формулы (5.53), (5.54), являются эмпирическими коэффициентами, учитывающими:
– средние напряжения цикла при изгибе и кручении. Остальные величины, входящие в формулы (5.53), (5.54), являются эмпирическими коэффициентами, учитывающими:
· 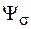 ,
, 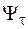 – влияние среднего напряжения на величину сопротивления усталости;
– влияние среднего напряжения на величину сопротивления усталости;
· 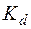 ,
, 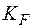 – масштабный фактор и степень шероховатости поверхности;
– масштабный фактор и степень шероховатости поверхности;
· 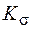 ,
, 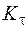 – влияние концентрации напряжений на сопротивление усталости.
– влияние концентрации напряжений на сопротивление усталости.
Эти коэффициенты в инженерных расчетах определяют по специальным справочникам. При решении рассматриваемой задачи студенты условно принимают значения этих коэффициентов по данным, приведенным в [4].
Дата добавления: 2015-03-07; просмотров: 625;
