Основные определения. В общем случае сложного сопротивления в стержне возникают все шесть видов внутренних усилий одновременно

В общем случае сложного сопротивления в стержне возникают все шесть видов внутренних усилий одновременно. Эти шесть усилий определяем, как обычно, методом сечений и строим эпюры усилий. При определении внутренних усилий используем правила знаков, описанные во вступительной части разд. 5 и поясняемые рис. 5.1. После определения внутренних усилий находим опасные сечения, а в опасных сечениях – опасные точки. Рассмотрим подробно, где расположены опасные точки в двух наиболее часто используемых сечениях: круглом и прямоугольном[10]. Выпишем формулы, необходимые для проверки прочности в этих точках.

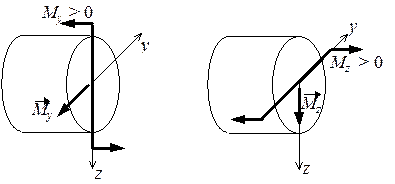Рис. 5.25. Изображение пар сил Мy и Мz в виде векторов

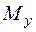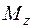Для определения положения опасных точек в круглом сечении построим эпюры распределения напряжений. Чтобы построить эпюру нормальных напряжений, вызванных двумя изгибающими моментами и , определим направление суммарного изгибающего момента. Изобразим пары 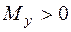и 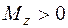в виде векторов, определяя их направление по правилу правого винта (рис. 5.25). Полный изгибающий момент является равнодействующей этих векторов и изображен на рис. 5.26. Поскольку для круглого сечения любая ось является главной, то в какой бы плоскости ни был приложен изгибающий момент, он вызывает плоский изгиб. Нейтральная линия в этом случае перпендикулярна плоскости изгиба, то есть совпадает с линией действия вектора полного изгибающего момента 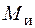. На рис. 5.26 показана эпюра нормальных напряжений, вызванных действием изгибающего момента 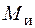. Кроме того, в сечении возникают нормальные напряжения от продольной силы N и касательные напряжения от крутящего момента 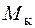. Эпюры распределения этих напряжений показаны на рис. 5.26[11]. Знаки напряжений соответствуют положительным значениям внутренних усилий. Видно, что опасными точками могут быть точки 1, 1¢, в которых действуют максимальные нормальные напряжения от изгиба и продольной силы и максимальные касательные напряжения, вызванные крутящим моментом. Для проверки прочности хрупких материалов важен знак нормальных напряжений (более опасной точкой будет, как правило, точка с растягивающими напряжениями), для пластичных материалов опасной будет точка, где нормальные напряжения от изгиба и продольной силы имеют одинаковые знаки. Опасные точки находятся в "балочном" напряженном состоянии, и проверку прочности в них следует осуществлять по теориям прочности, соответствующим материалу стержня. Приведем условия прочности, справедливые для "балочного" напряженного состояния, по двум наиболее часто используемым теориям:

· для хрупких материалов – теория Мора

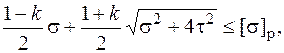(5.30)

где ;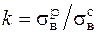

Рис. 5.26. Эпюры распределения напряжений в стержне круглого сечения

· для пластичных материалов – третья теория прочности

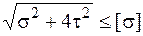. (5.31)

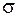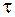В формулах (5.30), (5.31) и – напряжения в опасных точках.

В точках 1, 1¢ круглого сечения эти напряжения определяются так:

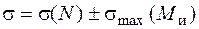; (5.32)

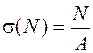; (5.33)

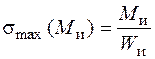; (5.34)

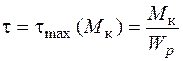, (5.35)

где 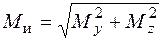; ; 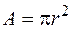; 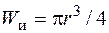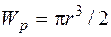. Поясним выбор знака в формуле (5.32). В рассматриваемой задаче в точке 1 складываются растягивающие напряжения от изгиба и продольной силы, в точке 1’ от растягивающих напряжений, вызанных N, вычитаются сжимающие напряжения от М_и.

При подборе сечения обычно пренебрегают влиянием продольной силы. В этом случае условия прочности (5.30) и (5.31) для круглого сечения с учетом формул (5.34) и (5.35) можно преобразовать. Теория Мора приобретает такой вид:

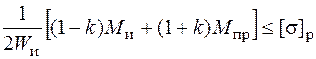, (5.36)

а третья теория прочности приводится к следующему условию:

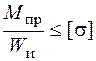, (5.37)

где 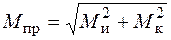. Из условий прочности (5.36), (5.37) можно найти необходимый момент сопротивления, а далее радиус поперечного сечения. Чтобы учесть продольную силу, немного увеличивают полученное значение радиуса (как правило, достаточно округления в большую сторону), находят напряжения по формулам (5.33)–(5.35) и проверяют прочность с учетом 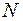по условиям (5.30) или (5.31).

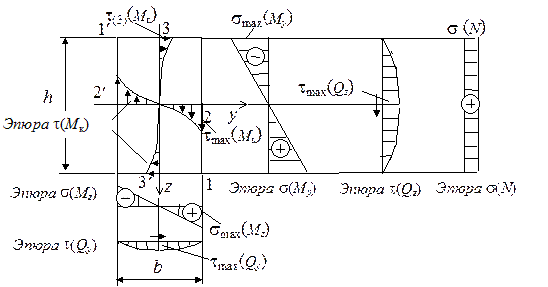Рис. 5.27. Эпюры распределения напряжений в стержне прямоугольного сечения

Построим эпюры распределения напряжений от всех усилий в прямоугольном сечении и определим положение опасных точек. Эти эпюры изображены на рис. 5.27, где знаки и направления напряжений соответствуют положительным внутренним усилиям. Из рис. 5.27 следует, что в прямоугольном сечении в общем случае опасными могут быть три группы точек:

· точки 1, 1¢ с максимальными нормальными напряжениями (для хрупких материалов важна не только величина напряжения, но и его знак). Напряжения в них

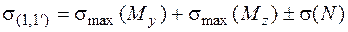; (5.38)

Согласно рис. 5.27 в точке 1 складываются растягивающие напряжения от всех усилий (М_y, M_z и N). В точке 1¢ от сжимающих напряжений, вызванных изгибающими моментами, вычитаются растягивающие напряжения от продольной силы.

· точки 2, 2¢ – в них действуют нормальные напряжения от 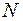, максимальные нормальные напряжения от 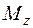и максимальные касательные напряжения, вызванные крутящим моментом и поперечной силой :

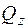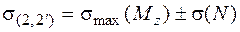, (5.39)

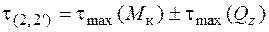; (5.40)

· точки 3, 3¢ с нормальными напряжениями от 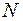, максимальными нормальными напряжениями от 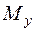и, кроме того, в этих точках действуют касательные напряжения от кручения и максимальные касательные напряжения, вызванные поперечной силой :

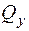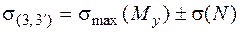, (5.41)

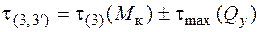. (5.42)

В зависимости от величин и знаков внутренних усилий необходимо выбрать самые опасные точки и проверить в них прочность. Знаки "плюс" или "минус" в формулах (5.38)–(5.42) выбираются в зависимости от направления напряжений в рассматриваемой точке. При этом в точках 2, 2¢ или 3, 3¢ хотя бы для одного напряжения ( 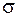или 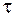) направления должны совпадать.

В точке 1, где нормальные напряжения от 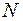, 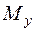и 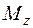имеют одинаковый знак, условие прочности записывается так:

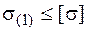, (5.43)

так как эта точка находится в линейном напряженном состоянии. Для хрупких материалов в правой части неравенства стоит 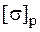или 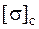в зависимости от направления напряжения. Точки 2 (2¢) и 3 (3¢) находятся в "балочном" напряженном состоянии и условие прочности в них записывается по формулам (5.30) или (5.31) в зависимости от материала. Для хрупких материалов наиболее опасными являются точки, в которых действуют растягивающие напряжения, для пластичных материалов это точки с максимальными по модулю нормальными напряжениями.

В формулах (5.38)–(5.42)

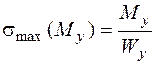; (5.44)

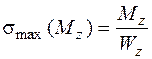; (5.45)

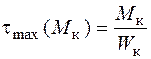; (5.46)

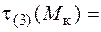
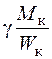; (5.47)

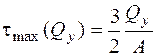; (5.48)

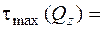
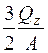; (5.49)

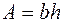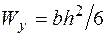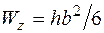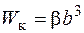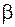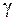; ; ; . Коэффициенты и определяются по таблице и зависят от 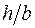. В приведенных формулах 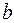– меньшая сторона прямоугольника, параллельная оси 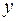. Знаки усилий в формулах (5.33)–(5.35) и (5.44)–(5.49) не учитываются.

Подбор размеров прямоугольного сечения производят из условия прочности в угловой точке без учета продольной силы. Перед подбором размеров сечение стержня надо расположить рационально. Если 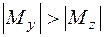, то наибольшая сторона 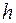должна быть перпендикулярна оси 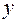. В этом случае 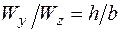; 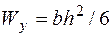. В противном случае сторона 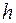должна быть расположена параллельно оси 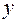, , 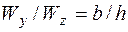а 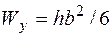. Условие прочности (5.43) в угловой точке без учета 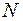записывается следующим образом:

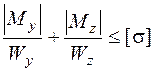. (5.50)

Зная отношение моментов сопротивления 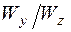, из (5.50) можно найти необходимую величину момента сопротивления, а далее размеры сечения. Для учета продольной силы обычно округляют полученные размеры в большую сторону и проверяют прочность во всех опасных точках прямоугольного сечения с учетом всех усилий по приведенным выше формулам.