Затухающие колебания.

Во всякой реальной колебательной системе имеются силы сопротивления, под действием которых колебания будут затухать. При достаточно малых скоростях движения сила сопротивления 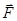пропорциональна скорости 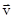( 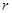- коэффициент сопротивления среды):

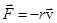
или в проекции на ось :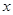

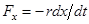
Знак минус обусловлен тем, что сила 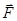и скорость 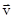имеют противоположное направление.

По второму закону Ньютона найдем уравнение затухающих колебаний:

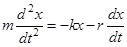(6)

Решением уравнения движения (6) является функция (закон движения)

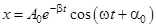(7)

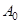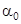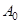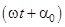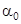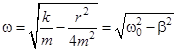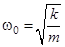Постоянные и могут быть любыми, в зависимости от начальных условий движения. Отметим, что - это начальная амплитуда; b - коэффициент затухания; - фаза колебания, а - начальная фаза колебания, , где , а 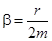. Коэффициент b характеризует скорость затухания колебаний, т.е. уменьшение амплитуды за единицу времени.

Если коэффициент затухания системы очень большой, то может выполниться условие 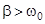. В этом случае гармонических колебаний не возникнет, а будет наблюдаться апериодическое движение груза.

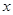На рис.4 представлен график зависимости от 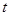для затухающих колебаний.

Быстроту затухания в зависимости от числа колебаний характеризуют логарифмическим декрементом затухания. Логарифмический декремент затухания q равен натуральному логарифму отношения двух соседних амплитуд одного знака:

.

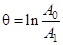Если известна 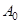- начальная амплитуда и 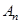- амплитуда через 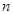периодов (или через 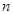полных колебаний), то логарифмический декремент затухания

.

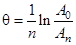Коэффициент затухания b характеризует затухание колебаний за единицу времени, а логарифмический декремент затухания q - затухание колебаний за период, следовательно: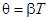

Определение показателя адиабаты
методом Клемана и Дезорма

Цель работы:определить показатель адиабаты и сравнить его величину с теоретическим значением.