Описание установки. В данной работе маятник представляет собой пружину малой массы с грузом массы на ее конце (см.рис.1)
 В данной работе маятник представляет собой пружину малой массы с грузом массы
В данной работе маятник представляет собой пружину малой массы с грузом массы 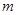 на ее конце (см.рис.1). Выведенный из положения равновесия и предоставленный самому себе груз маятника будет совершать собственные колебания. Сопротивление воздуха сравнительно невелико и его можно не учитывать. Тогда период колебаний груза определяется формулой:
на ее конце (см.рис.1). Выведенный из положения равновесия и предоставленный самому себе груз маятника будет совершать собственные колебания. Сопротивление воздуха сравнительно невелико и его можно не учитывать. Тогда период колебаний груза определяется формулой:
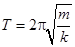 (1)
(1)
где 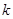 - коэффициент упругости пружины.
- коэффициент упругости пружины.
Коэффициент упругости пружины 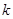 можно найти статическим методом. Если
можно найти статическим методом. Если 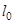 - длина пружины в ненагруженном состоянии, а
- длина пружины в ненагруженном состоянии, а 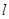 - длина пружины с грузом в состоянии равновесия, то в этом случае модуль силы тяжести
- длина пружины с грузом в состоянии равновесия, то в этом случае модуль силы тяжести 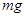 равен модулю силы упругости
равен модулю силы упругости 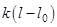 ;
;
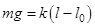 , откуда
, откуда 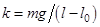 (2)
(2)
Коэффициент 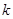 численно равен силе, которую нужно приложить к пружине при упругой деформации, чтобы растянуть (или сжать) пружину на единицу длины.
численно равен силе, которую нужно приложить к пружине при упругой деформации, чтобы растянуть (или сжать) пружину на единицу длины.
Из формулы (1) имеем
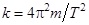 (3)
(3)
Выражение (3) позволяет определить значение 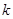 динамическим способом и предоставляет возможность сравнить его со значением, полученным статическим методом по формуле (2).
динамическим способом и предоставляет возможность сравнить его со значением, полученным статическим методом по формуле (2).
На пружине, расположенной слева на рис.1, изучаются затухающие колебания груза в жидкости. Опытным путем определяются период колебаний, начальная 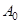 и через
и через 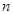 колебаний
колебаний 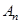 амплитуды и подсчитывается логарифмический декремент затухания q, коэффициент затухания b и коэффициент сопротивления
амплитуды и подсчитывается логарифмический декремент затухания q, коэффициент затухания b и коэффициент сопротивления 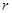
Дата добавления: 2015-03-07; просмотров: 630;
