Гармонические колебания.

Теоретическое введение.Пружинным маятником называют колебательную систему, представляющую собой материальную точку массой , закрепленную на одном конце спиральной пружины, другой конец которой неподвижен (пружина может находиться как в вертикальном, так и в горизонтальном положении). Причем в простейшем случае закрепленный конец пружины находится в покое относительно инерциальной системы отсчета, в которой происходят колебания маятника. Внутренними силами, которые вызывают колебательное движение пружинного маятника, являются силы упругости пружины.

Период колебаний пружинного маятника 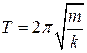, где — масса тела, 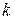— жесткость пружины. При точных расчетах периода и частоты колебаний пружинного маятника необходимо учитывать также массу пружины 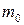. В этом случае , где .

Математический маятник — это колебательная система, состоящая из материальной точки массой , подвешенной на невесомой нерастяжимой нити длиной и способная совершать колебания в гравитационном поле Земли, или в другом силовом поле. В реальных условиях — это тело, масса которого во много раз больше массы нити, а размеры малы по сравнению с длиной нити (колебательная система состоит из материальной точки, нити и гравитационного поля Земли). Внутренней силой, вызывающей колебательное движение, является равнодействующая силы тяжести и силы упругости нити.

Если точка подвеса математического маятника покоится или движется равномерно прямолинейно относительно инерциальной системы отсчета, связанной с поверхностью Земли, то период малых колебаний математического маятника 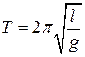, где 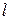— длина маятника, ускорение силы тяжести.

Формула для определения периода согласуется с экспериментальными законами малых колебаний математического маятника, которые были открыты Галилеем. Согласно этим законам, период малых колебаний математического маятника не зависит от амплитуды колебаний и массы маятника. Кроме того, этот период прямо пропорционален корню квадратному из длины маятника и обратно пропорционален корню квадратному из ускорения свободного падения.

Если точка подвеса математического маятника движется в гравитационном поле Земли с ускорением 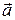, которое направлено под углом к ускорению силы тяжести , то период малых колебаний маятника определяется по формул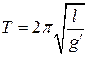е , где .

Цель опытов. Обеспечить овладение экспериментальными методами проверки законов колебаний пружинного и математического маятников и выяснение границ их применимости.