Теоретическое введение.

Термоэлектрические явления (явления Зеебека, Пельтье и Томсона) обусловлены наличием взаимосвязи между тепловыми и электрическими процессами в проводниках и полупроводниках.

Явление возникновения термоэлектродвижущей силы (термоэдс) было открыто в 1821г. немецким физиком Томасом Иоганном Зеебеком. Суть явления состоит в том, что в замкнутой электрической цепи, показанной на рис.1,

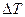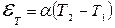, (1)

где 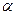- коэффициент пропорциональности, зависящий от природы контактирующих материалов, называемый удельной термоэдс.

В 1834г. французский физик Жан Шарль Пельтье обнаружил, что при прохождении тока в цепи из разнородных проводников, в местах контактов в дополнение к теплоте Джоуля выделяется или поглощается (в зависимости от направления тока), некоторое количество тепла, которое получило название теплота Пельтье. Явление Пельтье обратно явлению Зеебека. Как показывает опыт, теплота Пельтье пропорциональна количеству электричества (т.е. заряду q), протекающему через контакт:

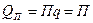It,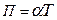

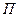- коэффициент Пельтье,

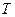- абсолютная температура.

Явление Томсона наблюдается в неравномерно нагретом однородном проводнике, при пропускании через него электрического тока. Если вдоль проводника, по которому проходит ток, устанавливается перепад температур 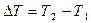, то в объёме проводника в дополнение к теплоте Джоуля выделяется или поглощается, в зависимости от направления тока, некоторое количество тепла (теплота Томсона):

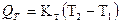It,

где K_т – коэффициент Томсона, зависящий от природы материала.

Все термоэлектрические явления можно достаточно хорошо объяснить с помощью элементарной квантовой теории. (Об энергетических уровнях электронов в металле, распределении электронов по уровням и энергии Ферми см. лаб. раб. 5). При контакте двух разнородных металлов возникают внешняя и внутренняя контактные разности потенциалов. Определим сначала, опираясь на квантовую теорию, внешнюю контактную разность потенциалов. Предположим, что энергии Ферми двух металлов равны друг другу 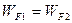(это существенно облегчает объяснение данного вопроса).

На рис. 2а изображены энергетические схемы двух металлов до контакта. За нулевой уровень принята потенциальная энергия покоящегося электрона, находящегося вне металла. Глубина потенциальной ямы определяется внутренней потенциальной энергией электрона 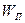. 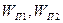- внутренние потенциальные энергии электронов в металлах; 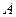₁ и 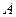₂ – работы выхода, 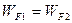= W_F - энергии Ферми.

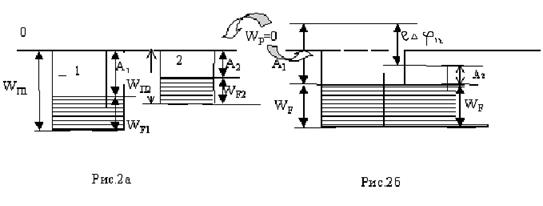
При контакте электроны получают возможность переходить из одного металла в другой. Так как в металле 2 электроны находятся на более высоких энергетических уровнях, то в соответствии с принципом наименьшей энергии, электроны из металла 2 будут переходить на более низкие уровни в металле 1. Металл 1 начнёт заряжаться отрицательно, а его положительный внутренний потенциал будет уменьшаться. В результате все уровни металла 1 сдвинутся вверх относительно нулевого уровня (рис. 2б). Во втором металле, который заряжается положительно, вся система сдвигается вниз, так как его положительный внутренний потенциал растёт. Напомним, что потенциал и потенциальная энергия электрона в нём имеют разные знаки. Этот процесс продолжается до тех пор, пока уровни Ферми в металлах не сравняются. Отметим, что сдвиг уровней происходит для всего металла в целом, а не только в контактном слое.

В первом металле электроны, перешедшие из второго металла, соберутся на его поверхности и создадут вне металла отрицательный потенциал (энергия электрона при этом положительна см. рис. 2б). У поверхности второго окажется положительный потенциал. Таким образом, между свободными концами металлов образуется внешняя контактная разность потенциалов равная, как видно на рисунке 2б:

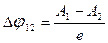, где е - модуль заряда электрона (2)

При этом в месте контакта, при условии: 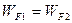в контактном слое поле отсутствует. Электроны свободно переходят из одного металла в другой.

Рассмотрим теперь случай, когда энергии Ферми металлов не равны друг другу рис. 3а. Тогда возникновения внешней контактной разности потенциалов не достаточно для равновесия. Пусть 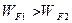, это означает, что и средняя кинетическая энергия электронов в первом металле, выше чем во втором. Эта разница энергий приводит к тому, что электроны первого металла, переходя во второй, приносят туда большую кинетическую энергию. Передача избытка энергии решетке второго металла приводит к его нагреванию. Но и в первый металл будут попадать электроны из второго металла, обладающие меньшей энергией Ферми - они будут охлаждать первый металл. Таким образом, самопроизвольно, между металлами появляется разность температур, - это противоречит второму закону термодинамики! Поэтому на границе металлов в контакте возникает разность потенциалов 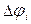, ускоряющая электроны, идущие из второго металла в первый и повышающая их кинетическую энергию до значения 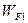, а также замедляющая электроны первого металла, идущие во второй. В результате их кинетическая энергия становится равной 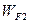. Поэтому в первом металле (с большей энергией Ферми 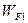) потенциал у контакта должен быть выше, чем во втором (рис. 3б).

Работа в контактном слое равна: 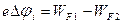, (3)

где 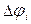- внутренняя контактная разность потенциалов.

В соответствии с (3) получим

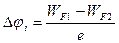. (4)

Внутренняя контактная разность потенциалов не только выравнивает кинетические энергии электронов приходящих в металл и электронов – хозяев, но и потоки электронов в ту и другую сторону.

Возникновение термоэдс в соответствии с квантовой теорией обусловлено тремя причинами:

1. Зависимостью уровня Ферми от температуры (см. лаб. раб. №5);

3. Диффузией носителя тока (эдс Томсона);

4. Увлечением электронов фононами – акустическими квантами энергии (этот эффект вносит вклад в термоэдс главным образом при низких температурах).

В наших расчётах в применении к данной лабораторной работе 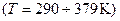влиянием последнего фактора можно пренебречь.

Рассмотрим физическую сущность первых двух механизмов. В первом случае в местах контактов (см. рис. 1) возникают внутренние контактные разности потенциалов, которые, при равенстве температур контактов, одинаковы по величине, но противоположны по знаку, Их сумма будет равна нулю. Если один из контактов нагреть, то энергия Ферми в каждом из металлов в месте контакта понизится (см. лаб. Раб. №5), уменьшится, в соответствии с формулой (3), и величина внутренней контактной разности потенциалов в этом контакте, оставаясь прежней по знаку. В результате сумма разностей потенциалов в каждом из контактов в такой цепи станет отличной от нуля. Появится термоЭДС.

Чтобы понять вторую причину возникновения термоэдс, рассмотрим отрезок проводника длиной 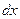, где имеется градиент температуры 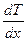.(см. Рис.4)

В возникновении разности потенциалов на концах проводника в этом случае играют роль два фактора.

1. Уровень Ферми 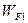на горячем конце лежит ниже, чем на холодном, 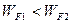, так как с повышением температуры энергия Ферми уменьшается. Поэтому электроны должны переходить из холодной части («холодные» электроны) в горячую часть проводника. Возникает поток электронов от холодной части к горячей.

2. Как правило, средний возбужденный уровень энергии в горячей части выше, чем в холодной (пунктирные уровни на рисунке) – это приводит к диффузии имеющих большую кинетическую энергию, т.е. более быстрых («горячих») электронов к холодному концу.

Таким образом возникает два встречных диффузионных потока электронов – «холодных» и «горячих». Однако скорость теплового движения вторых выше, чем первых. В результате от конца проводника с большей температурой уходит больше «горячих» электронов, чем приходит «холодных» и здесь накапливается положительный заряд, а на противоположном, менее нагретом конце, накапливается отрицательный заряд. Вследствие такого разделения зарядов в проводнике на его концах появится разность потенциалов, которая, складываясь с разностью потенциалов, возникающей вследствие действия первого механизма, дает суммарную термоЭДС. Расчёт, который из-за сложности мы не приводим, показывает, что при небольших разностях температур вклады от обоих механизмов оказываются пропорциональны разности температур контактов и при их сложении получается формула (1).

Термопары широко применяют в промышленности для измерения температур, особенно в тех случаях, где применение жидкостных термометров исключается. Достоинствами термопарных термометров являются высокая чувствительность, малые размеры, малая собственная, малые размеры, малая собственная теплоёмкость, большой диапазон измеряемых температур ( 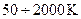), возможность присоединения к самописцам, автоматически регистрирующим температуру.

Термопары можно использовать и в качестве источников тока, для этого их соединяют последовательно в термобатарею. КПД полупроводниковых элементов достигает 15% и в дальнейшем, несомненно, будет повышен ёще больше. В развитых странах ведётся разработка полупроводниковых термоэлектрогенераторов для прямого преобразования в электрическую энергии солнца, ядерных реакторов и др.