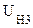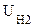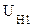Теоретическое введение
Термоэлектронной эмиссией называется испускание электронов твердым и некоторыми жидкими телами при их нагревании.
Рассмотрим возникновение термоэлектронной эмиссии в металлических проводниках. Металлические проводники можно представить как систему из колеблющихся около положений равновесия положительно заряженных ионов и относительно свободных электронов проводимости, перемещающихся между ионами кристаллической решетки. Существуют две причины возникновения сил на границы металла – вакуума, удерживающих свободные электроды в металле. По электронной теории эти электроны образуют “электронный газ”, а их тепловые скорости при данной температуре различны и распределены в соответствии с законом Максвелла. Это означает, что в металле всегда имеется некоторое число электронов, обладающих большими значениями скоростей, направленных в сторону поверхности металла. Такие электроны способны покинуть металл. Однако на поверхности металла при этом индуцируется положительный заряд. Сила взаимодействия его с электроном не позволяет удаляться последнему от поверхности на расстояние, превышающее 10-9 м, возвращая его обратно в металл (1-ая причина). Следовательно, при данной температуре металла над его поверхностью всегда имеется определенное число электронов, образующих “электронное облако”, находящееся в динамическом равновесии с электронным газом металла (число электронов покидающих металл равно числу электронов возвращающихся из облака в металл). Количество электронов над поверхностью металла зависит от природы металла и его температуры.
Электрическое поле, образованное двойным электрическим слоем – объемным отрицательным зарядом электронного облака и положительно заряженным металлом, препятствует выходу электронов из металла т.е. является тем потенциальным барьером, который должны преодолевать электроны при выходе из металла (2-ая причина). Для преодоления этого барьера кинетическая энергия электрона Wk = 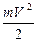 должна быть больше величины потенциального барьера, т.е. больше той работы, которую выполняет электрическое поле при торможении электрона.
должна быть больше величины потенциального барьера, т.е. больше той работы, которую выполняет электрическое поле при торможении электрона.
При перемещении электрона от наружного слоя ионов металлической решетки к электронному облаку потенциал поля двойного электрического слоя уменьшается, а потенциальная энергия электрона возрастает (W 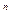 = -e×j). За пределами электронного облака потенциал поля и потенциальная энергия электрона резко стремиться к нулю (как за пределами пластин плоского конденсатора) W
= -e×j). За пределами электронного облака потенциал поля и потенциальная энергия электрона резко стремиться к нулю (как за пределами пластин плоского конденсатора) W 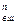 = 0. Преобладающее число валентных электронов потенциально не способно покинуть металл, поэтому можно считать, что металл для электронов представляет потенциальную яму, глубина которой равна разности потенциальных энергий электронов проводимости вне и внутри металла:
= 0. Преобладающее число валентных электронов потенциально не способно покинуть металл, поэтому можно считать, что металл для электронов представляет потенциальную яму, глубина которой равна разности потенциальных энергий электронов проводимости вне и внутри металла: 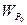 = W
= W 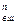 - W
- W 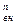 (см. рис. 1). Плоское дно потенциальной ямы означает, что весь объем металла эквипотенциален. Стенки ямы можно считать вертикальными, т. к. скачок потенциальной энергии происходит на длине порядка нескольких межатомных расстояний (
(см. рис. 1). Плоское дно потенциальной ямы означает, что весь объем металла эквипотенциален. Стенки ямы можно считать вертикальными, т. к. скачок потенциальной энергии происходит на длине порядка нескольких межатомных расстояний ( 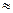 10-9м).
10-9м).
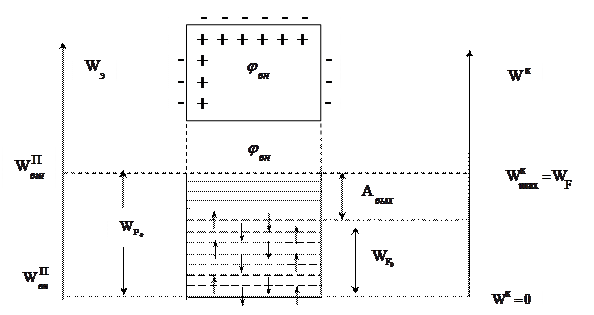
Рис.1
Полная энергия электрона W 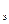 внутри металла равна сумме его кинетической W
внутри металла равна сумме его кинетической W 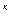 и потенциальной W
и потенциальной W 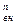 энергий:
энергий:
W 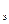 = W
= W 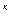 + W
+ W 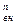 . (1)
. (1)
Причем, во всех точках внутри металла W 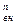 = const, т. к. j= const.
= const, т. к. j= const.
Если бы электронный газ был подобен идеальному, то при Т = 0К , в соответствии с распределением Максвелла, скорости, а, следовательно, и кинетические энергии всех электронов были бы равны нулю и W 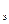 = W
= W 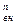 . При этом все электроны находились бы на дне потенциальной ямы. Работа выхода в этом случае равна глубине потенциальной ямы. В действительности они различны. Например, для никеля Авых =5 эВ, а Wp0=14 – 17 эВ.
. При этом все электроны находились бы на дне потенциальной ямы. Работа выхода в этом случае равна глубине потенциальной ямы. В действительности они различны. Например, для никеля Авых =5 эВ, а Wp0=14 – 17 эВ.
Такое расхождение объясняется тем, что электронный газ в металле подчиняется не классической статистике Максвелла – Больцмана, а квантовой статистике Ферми – Дирака. Вследствие этого кинетическая энергия электронов в рассматриваемой модели может иметь только дискретные значения. Эти значения называют энергетическими уровнями. Если электрон обладает данным значением кинетической энергии, то это значит, что он находится на соответствующем энергетическом уровне.
Распределение электронов проводимости в металле по энергиям осуществляется согласно двух принципов: принцип наименьшей энергии – электроны в первую очередь занимают состояния с наименьшей энергией; и принципа запрета Паули – в каждом состоянии с данной энергией может находиться не более двух электронов, у которых собственные моменты импульсов (спины) направлены в противоположные стороны. Из–за квантового принципа запрета Паули даже при температуре Т = 0К значения кинетической энергии электронов проводимости заключены в пределах 0 до W 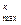 . Максимальная кинетическая энергия, которой обладают электроны в металле при абсолютном нуле, называется энергией Ферми и обозначается
. Максимальная кинетическая энергия, которой обладают электроны в металле при абсолютном нуле, называется энергией Ферми и обозначается 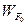
При 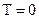 K энергия Ферми равна:
K энергия Ферми равна: 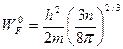 ,где
,где 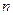 - концентрация валентных электронов, h-постоянная Планка.
- концентрация валентных электронов, h-постоянная Планка.
Энергия Ферми слабо зависит от температуры: 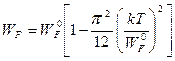 ,
,
где 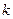 - постоянная Больцмана.
- постоянная Больцмана.
Энергетический уровень, соответствующий энергии Ферми называется уровнем Ферми. Из статистики Ферми-Дирака следует, что вероятность заполнения этого уровня электронами равняется 0,5.
Полная энергия электронов, в соответствие с формулой (1), равна сумме их кинетических и потенциальных энергий. Ее найдем, если впишем энергетические уровни электронов в металле в потенциальную яму (рис.1). Тогда положение уровня относительно дна потенциальной ямы дает кинетическую энергию соответствующего электрона, а его положение на шкале энергий относительно 0 – сумму кинетической и потенциальной энергий, то есть полную энергию ( пунктиром изображены не занятые при 0 К уровни). Для электронов в металле она отрицательна.
Полная работа выхода электронов в квантовой механике, как и в классической, остается равной глубине потенциальной ямы Wp0. Однако даже при абсолютном нуле температуры они обладают большой кинетической энергией. Для удаления электрона из металла ему необходимо сообщить добавочную энергию, равную по модулю полной энергии электрона. Тогда он перейдет на самый высокий уровень и сможет покинуть потенциальную яму, то есть станет свободным. В соответствие с рис. 1 значение добавочной энергии для разных электронов различно. Ее значение минимально для электронов, находящихся на уровне Ферми. Эмиссия электронов при нагревании начнется тогда, когда добавочную энергию получат электроны, находящиеся на уровне Ферми. Поэтому в квантовой теории работой выхода называют наименьшую добавочную энергию, которую необходимо сообщить электрону для того, чтобы удалить его из металла в вакуум. В соответствие со сказанным наименьшей она будет для электронов, находящихся на уровне Ферми, и для работы выхода электронов из металла получим следующую формулу
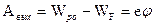 , (2).
, (2).
где j - потенциал выхода.
При других температурах металла (Т >0 К ) работу выхода также определяют в соответствии с уравнением (2).
Энергия Ферми и работа выхода электрона из металла являются характеристиками данного металла и слабо зависят от температуры. Величина работы выхода очень чувствительна к присутствию на поверхности металла примесных атомов: например, нанесение на поверхность вольфрама слоя окисла щелочноземельного металла (Са, Sr, Ba.) снизит работу выхода с 4,5 эВ (для чистого вольфрама) до 1,5 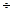 2,0 эВ.
2,0 эВ.
Принятой единицей измерения работы выхода является электрон-вольт (эВ),численно равный работе, выполненной электрическим полем над электроном, прошедшим разность потенциалов в 1 В:
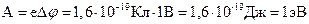
Закономерности в явлении термоэлектронной эмиссии удобно исследовать с помощью электровакуумного диода, включенного в электрическую цепь, изображенную на рис. 3
Электровакуумный диод представляет собой металлический или стеклянный вакуумированный баллон, в который впаяны два электрода – катод и анод. Источником свободных электронов в диоде является катод, эмиссия с поверхности которого происходит в результате разогрева катода током накала.
Катод косвенного накала в диоде типа 6Х6С выполнен в форме металлического цилиндра, на наружную поверхность которого нанесен слой оксидов для уменьшения работы выхода электронов (для улучшения эмиссионной характеристики катода). Внутри цилиндра помещена свернутая в спираль нить накала, покрытая жароупорным (температура катода превышает 1000о С) электроизоляционным веществом, не имеющая электрического соединения с катодом. Для разогрева катода по нити пропускают ток накала постоянной или переменной величины (Iн).
Так как анод является приемником движущихся от катода электронов, то его изготовляют из тугоплавкого материала. Анод выполняется в форме цилиндра, окружающего катод.
Для выявления особенностей работы диода и закономерностей термоэлектронной эмиссии снимается семейство вольт – амперных характеристик (ВАХ), каждая из которых показывает зависимость анодного тока Ia(тока, протекающего через диод), от анодного напряжения Ua ( разности потенциалов между катодом и анодом ) при постоянной температуре катода ( ток накала IH = const ). Три такие характеристики при различных температурах катода приведены на рис. 2а.
При анализе особенностей ВАХ помним, что для данного катода число электронов вылетевших из катода в единицу времени зависит только от температуры катода (т.е. от величины тока накала IH ), а число электронов долетевших до анода в единицу времени (т.е. Ia ) зависит еще и от величины и направления электрического поля между катодом и анодом (т. е. от величины и знака Uа ).
а) б)
Рис. 2
При Ua = 0 небольшая часть испускаемых катодом электронов преодолевает действие тормозящего их электрического поля двойного слоя и достигает анода, поэтому Ia>0.
При Ua = -Uзап (потенциал анода меньше потенциала катода) анодный ток отсутствует Ia= 0.
При анодных напряжениях 0 < Ua < Uнас конфигурация электрического поля в межэлектродном пространстве сложна и такова, что потенциал поля проходит через минимум вблизи катода (рис. 2б). Величина и положение jmin определяется эмиссионной характеристикой катода и анодным напряжением. С ростом анодного напряжения минимум потенциала перемещается к катоду и значение его уменьшается по абсолютной величине. Это приводит к понижению потенциального барьера для эмитируемых электронов, и все большее их количество достигает анода, а все меньше возвращается в катод.
Когда минимум потенциала достигает катода (при Ua = Uнас), электрическое поле между катодом и анодом во всех точках станет ускоряющим и все электроны, испускаемые катодом, будут достигать анода. Дальнейший рост Ua не может увеличить силу анодного тока – ток достигает насыщения, Ia=Iнас (пунктирная линия графика Ia=f(Ua) (об эффекте Шоттки ниже).
Диод обладает нелинейной вольт – амперной характеристикой. Зависимость анодного тока от анодного напряжения на участке АВ характеристики описывается “ законом трех вторых”, полученным Ленгмюром и Богуславским:
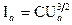 (3).
(3).
где С – коэффициент, зависящий от формы электродов и их взаимного расположения.
Термоэмиссионные свойства катода характеризуются величиной тока насыщения 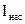 . Измеряя плотность тока насыщения
. Измеряя плотность тока насыщения 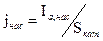 при различной силе тока накала, можно найти количество электронов, вылетающих с единицы поверхности катода при разных температурах. Здесь Sкатода - площадь поверхности катода.
при различной силе тока накала, можно найти количество электронов, вылетающих с единицы поверхности катода при разных температурах. Здесь Sкатода - площадь поверхности катода.
Предполагая, что электроны в металле подчиняются квантовой статистике Ферми – Дирака, можно показать, что плотность тока насыщения зависит от температуры согласно формуле Ричардсона – Дэшмана:
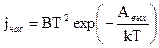 (4).
(4).
где В – эмиссионная постоянная, не зависящая от материала катода,
Авых – работа выхода электронов из металла. Из формулы (4) видно, что уменьшение работы выхода в несколько раз приводит к увеличению плотности тока насыщения в миллионы раз. Поэтому никелевые катоды покрываются окисью бария или стронция и имеют Aвых = 1,0 –1.2 эВ.
Выше отмечалось, что при анодных напряжениях Ua > Uнас сила анодного тока увеличиваться не должна. Однако в реальных вольт – амперных кривых наблюдается некоторое увеличение Ia с ростом Ua из – за эффекта Шоттки, который заключается в слабом уменьшении величины потенциального барьера и, следовательно, работы выхода при возрастании напряженности электрического поля между катодом и анодом.
Односторонняя проводимость диодов позволяет использовать их для выпрямления переменного тока.
Выполнение работы и обработка результатов эксперимента.
Упражнение 1. Снятие семейства вольт – амперных характеристик диода 6Х6С для различных температур катода.
1) 
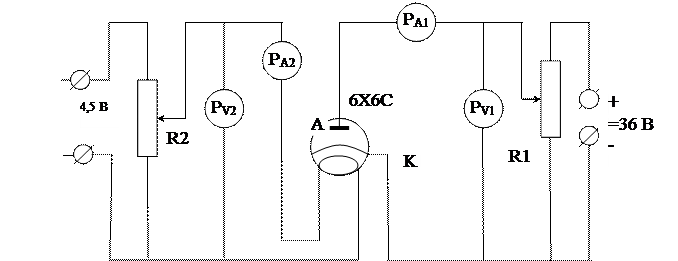
Собрать электрическую цепь по схеме на рис.3.
|
Анодная цепь состоит из амперметра PA1 (рис 3.), вольтметра PV1 и реостата R1, источник питания 36 В ( щиток на стене ).
Цепь накала включает в себя амперметр PA2, вольтметр PV2, реостат R2, и выпрямитель на 4,5 В. Причем R1 и R2 используются как потенциометры.
2) Определить цену деления электроизмерительных приборов.
3) Установить подвижные контакты потенциометров R1 и R2 так, чтобы анодное и накальное напряжение были равны нулю.
4) Включить выпрямитель и реостатом R2 установить напряжение накала Uн1, указанной на прилагаемой к установке электрической схеме. Записать величину тока накала 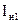 .
.
5) Включить источник анодного напряжения (включатель на щитке) и, задавая реостатом R1 указанные в таблице 1 значения анодного напряжения 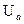 , измерить соответствующее значение анодного тока
, измерить соответствующее значение анодного тока 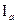 , занося их в таблицу 1.
, занося их в таблицу 1.
Таблица 1. 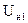 = …… В.
= …… В. 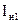 = …… А.
= …… А.
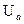 , В , В
| 0,2 | 0,6 | 1,0 | 3,0 | 5,0 | 7,0 | 9,0 | 11,0 | 13,0 | 15,0 |
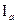 , А , А
|
6) Аналогичные измерения провести еще для двух значений накального напряжения, указанных преподавателем.
Таблица 2. 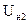 = …… В.
= …… В. 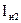 = …… А.
= …… А.
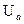 , В , В
| 0,2 | 0,6 | 1,0 | 3,0 | 5,0 | 7,0 | 9,0 | 11,0 | 13,0 | 15,0 |
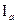 , А , А
|
Таблица 3. 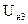 = …… В.
= …… В. 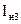 = …… А.
= …… А.
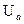 , В , В
| 0,2 | 0,6 | 1,0 | 3,0 | 5,0 | 7,0 | 9,0 | 11,0 | 13,0 | 15,0 |
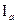 , А , А
|
7) На миллиметровой бумаге форматом 20´16 см. построить семейство вольт-амперных характеристик. Для примера семейство ВАХ изображено на рисунке 4.
 | |||||
| |||||
 | |||||
| |||||||
 |  |  | |||||


 100
100
 |
|
0 5 10 15
Рис. 4
Упражнение 2.Экспериментальная проверка формулы Ричардсона – Дэшмана и определение работы выхода электронов из катода.
Используя определение плотности тока, запишем: 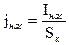 ;
;
где S – площадь поверхности катода;
Тогда уравнение Ричардсона – Дэшмана примет вид 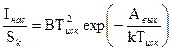
где 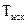 - температура катода при заданном
- температура катода при заданном 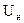 . После логарифмирования:
. После логарифмирования:
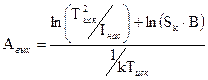 (5)
(5)
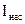 определяется путем экстраполяции линейных участков вольтамперных характеристик (ВАХ) диода на ось анодного тока (см. упр. 1, рис. 4).
определяется путем экстраполяции линейных участков вольтамперных характеристик (ВАХ) диода на ось анодного тока (см. упр. 1, рис. 4).
Для вычисления 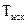 рабочая формула получается при использовании зависимости сопротивления проводника от его абсолютной температуры и закона Ома:
рабочая формула получается при использовании зависимости сопротивления проводника от его абсолютной температуры и закона Ома:
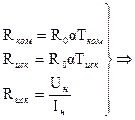
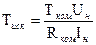
Значение 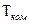 и
и 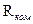 заданы на прилагаемой в практикуме схеме.
заданы на прилагаемой в практикуме схеме.
Дата добавления: 2015-03-07; просмотров: 1085;