БИОХИМИЯ КРОВИ.

Понятие тензора (от латинского tendo — напрягаю, растягиваю) принадлежит к числу основных, фундаментальных математических понятий и широко применяется сейчас в механике, электродинамике, теории относительности и т. д. Первоначально возникшее в рабо­тах XIX века по теории упругости, оно было систематически иссле­довано в 1886 —1901 гг. итальянским геометром Г. Рйччи-Курбастро (1853—1925) и итальянским математиком и механиком Т. Лёви-Чивйта (1873—1942).

Внимание к новому аппарату существенно возросло после создания в 1915 —1916 гг. великим ученым, физиком А. Эйнштейном (1879 — 1955) общей теории относительности, мате­матическая часть которой целиком основана на тензорном исчислении. Физические величины, которые нам встре­чались до сих пор, были либо скалярными, либо векторными. Однако существуют физические величины более сложной природы.

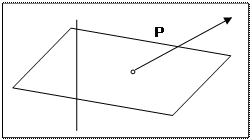
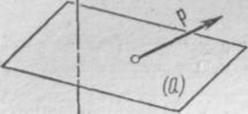
Например, однородное напряженное состоя­ние упругого тела характеризуется плотностью р силы, с которой одна часть тела действует на другую через мысленно вы­деленную плоскость (Q) (рис. 1); однако при этом р для различных направлений плоскости (Q) будет различным. Таким образом, вели­чина, характеризующая напряженное состояние, уже не является вектором, она представляет собой тензор 2-го ранга. Оказывается, что и многие другие важные величины, характеризующие состояние сплошных сред, также являются тен­зорами.

К настоящему времени тензорная алгебра, а также тензорный анализ (т. е. теория тензорных полей, связанная с применением диф­ференцирования и интегрирования) представляют собой значительно разработанные дисциплины.

§ 1. Тензорная алгебра

1. Примеры.К понятию тензора можно прийти уже размышляя над описанием векторов в обычном пространстве с помощью чисел. Как известно из векторной алгебры, все действия над векторами удобно осуществлять, выбрав евклидов базис i, j, k, после чего можно любой вектор а разложить по этому базису

а = а_хi + а_уj+ a_zk (1)

и взамен действий над векторами осуществлять действия над их про­екциями, т. е. над числами — коэффициентами разложений. Более того, даже задавать конкретные векторы обычно бывает удобнее с помощью разложения (1), чем каким-то геометрическим способом.

Однако задумаемся теперь, что это за векторы i, j, k. В некото­рых случаях, когда в задаче имеется естественная система отсчета направлений (например, во многих задачах статики), эти векторы можно описать вполне точно, «привязав» их к данным задачи. Но во многих случаях привлечение такой «абсолютной» системы отсчета является весьма искусственным либо вообще невозможно. Тогда по­лучается на первый взгляд парадокс: мы пользуемся проекциями вполне определенного вектора, которые зависят от выбора базиса, но не уточняем, как этот базис выбирается...

Эта трудность будет преодолена, если с самого начала отка­заться от выбора какого-то одного базиса, а считать, что все ба­зисы равноправны и каждому выбору базиса i, j, k отвечает на­бор значений а_х, а_у, а_z в соответствии с формулой (1). Подобный набор величин, приобретающих определенные значения лишь после выбора базиса и преобразующихся по определенному правилу при за­мене базиса (см. ниже), и называется тензором (или тензорной вели­чиной), а сами эти величины, составляющие в определенном порядке тензор, называются его компонентами. (Отметим некоторое несо­ответствие: в векторной алгебре принято компонентами вектора A называть в е к торы а_хi, а_уj, a_zk. Однако здесь мы будем компонентами называть величины а_х, а_y , а_z.)

В тензорном исчислении принято не писать знак суммы по повто­ряющемуся индексу, а при повторении индекса всегда осуществлять такое суммирование, т. е. писать последнюю формулу.

Здесь индекс суммирования является немым и может быть обозна­чен любой буквой, а пределы суммирования определяются размер­ностью пространства, в котором рассматривается тензор.

Напряженное состояние в окрестности точки

Если через произвольную точку тела провести три взаимно перпендикулярные площадки параллельно координат­ным плоскостям, то девять составляющих (компонент) напря­жения: три нормальных а_х, а_у, ст_г и шесть касательных х_ху, т,₂, т_2Х, т_ух, t_xz, х_zy, действующих на этих площадках (рис. 4.1),

полностью определяют напряженное состояние в окрестности данной точки. Это означает, что, зная эти девять величин, можно найти напряжения на любой наклонной площадке, проходя­щей через данную точку. Слово «со­ставляющая» или «компонента» в дальнейшем для краткости будем опускать.

Все девять напряжений можно обозначить одинаково, например, Gij{hj=x, У, z). Тогда при г'=у получа­ются нормальные напряжения, в которых сохраняется только один индекс, а при i Ф]—касательные напряжения. Первый индекс указывает, параллельно какой оси направлено напряже­ние, а второй обозначает нормаль к площадке, на которой оно действует. Это правило непосредственно относится к касатель­ным напряжениям, но им также можно пользоваться и для нормальных напряжений, если употреблять обозначения <у_и.

Нормальные напряжения считаются положительными, если они направлены в сторону внешней Нормали к площадке, и наоборот. В соответствии с этим правилом положительные нормальные напряжения считаются растягивающими, а от­рицательные — сжимающими.

Для касательных напряжений принимается следующее правило знаков. На площадке, внешняя нормаль к которой направленав положительном (или отрица­тельном) направлении соответст­вующей оси, касательное напряже­ние считается положительным, ес­ли оно также направлено в поло­жительном (или отрицательном) направлении оси. На рис. 4.1 пока­заны положительные напряжения.

Проведем вблизи точки О тела произвольную наклонную площад­ку ABC, площадь которой обозна­чим через dF(рис. 4.2). Положение этой площадки может быть опреде­лено углами, которые составляет нормаль v с осями координат.

Как известно из аналитической геометрии, направляющие косинусы нормали связаны между собой соотношением

l² + m²+n² = 1. (4.1)

Полное напряжение p_v, действующее на этой площадке, можно спроектировать на оси координат. Проекции p_xv, p_yv, p_zv определяются из уравнений равновесия тетраэдра ОАВС. Составим сумму проекций всех сил, приложенных к граням тетраэдра, на ось Ох (на рис. 4.2 на вертикальных и горизон­тальной гранях тетраэдра показаны только те напряжения, которые дают проекции на ось

БИОХИМИЯ КРОВИ.

В спортивной практике анализ крови используется для оценки влияния на организм спортсмена тренировочных и соревновательных нагрузок, оценки функционального состояния спортсмена и его здоровья. Информация, полученная при исследовании крови, помогает тренеру управлять тренировочным процессом. Поэтому специалист в области физической культуры должен иметь необходимые представления о химическом составе крови и об его изменениях под воздействием физических нагрузок различного характера.