ЛЕКЦИЯ 4

4. Расчёт и проектирование переходных кривых

Переходные кривые обеспечивают плавность входа подвижного состава в кривые за счет плавного нарастания кривизны.
При изменении радиуса от ¥ в НПК до радиуса круговой криво R в КПК.
В переделах переходной кривой также плавно увеличивается возвышение наружного рельса от 0 до h.

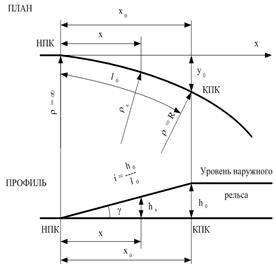
Центробежная сила, возникающая в любой точке переходной кривой, должна уравновешиваться центростремительной, возникающей за счет наличия возвышения наружного рельса.

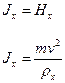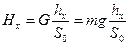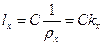Это требование будет выполнено, если кривизна будет нарастать пропорционально увеличению длины переходной кривой.

где С=Rl0 – параметр кривой.

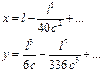Этому уравнению удовлетворяет кривая, называемая радиоидальной спиралью. В прямоугольной системе координат она имеет вид:

Если ограничиться двумя членами ряда, получим:

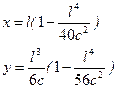Во многих случаях представляется возможным ограничиться первыми членами рядов и использовать уравлениня кубической параболы

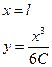
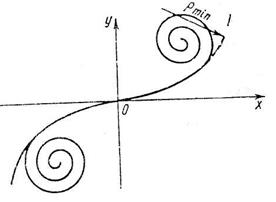
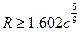Кубическая парабола отличается от радиоидальной спирали тем, что ее кривизна меняется пропорционально не протяжению переходной кривой, а ее проекции на ось Х.
Кубическая парабола может быть применена для разбивки переходной кривой, если выполняется требование:

Длина переходной кривой l0 определяется из условия обеспечения плавного отвода возвышения наружного рельса, принятого в круговой кривой, и безопасного подъема колеса, идущего по возвышению наружного рельса.

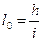При прямолинейном отводе возвышение наружного рельса длина переходной кривой определяется по зависимости

где i – уклон отвода возвышения наружного рельса, применяется по таблице

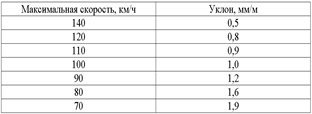
Длина переходной кривой принимается кратной 10 м и не должна быть короче 20 м

По второму условию ограничивается скорость нарастания непогашенного горизонтального ускорения aн за время прохождения переходной кривой

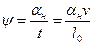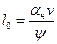откуда

Обычно принимают допускаемые значения a[н]=0,7 м/с2, ]Y[=0,6 м/с3

При этом получается l0=1.17 vmax

Если принять l0=h/i и v®км/ч, h®мм, получим

Обычно это требование выполняется.