Лекция 5. Разбивка переходных кривых

Разбивка переходных кривых

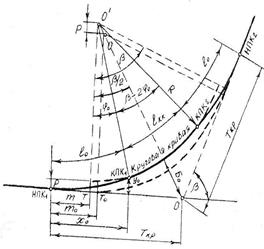
Наиболее распространенным является способ сдвижки круговой кривой во внутрь к центру. От имеющегося на местности тангенсного столика Т0 откладывают расстояние m0 и получают начало переходной кривой НПК.
Переходную кривую строят по ординатам в соответствии с ее уравнением, задаваясь значениями х=10; 20 и до х0.

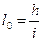Для этого принимается такая последовательность расчета.

1. Определяют длину переходной кривой и параметр С=Rl0.
2. Принимают вид переходной кривой (кубическую параболу или радиоидальную спираль). Кубическую параболу применяют при условии

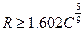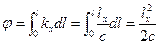3. Определяют угол поворота на протяжении переходной кривой

Для конца переходной кривой

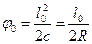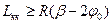4. Определяют возможность разбивки переходных кривых по условию 2j0<b,
где b - угол поворота трассы.
Возможность устройства переходных кривых длиной l0 при угле поворота линии b определяется тем, чтобы длина круговой кривой была не менее некоторого минимума.

где Lкк – длина круговой кривой; Lкк³ 30 м.
Если требования не выполняются, разбивка невозможна – надо менять исходные параметры:
R, l0, С.

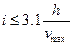Для разбивки переходной кривой необходимо определить:
5. Расстояние от начала переходной кривой до нового положения тангенсного столбика
m=x0-R sinj0

6. Сдвижку круговой кривой к центру
Р=y0-R(1-cosj0)
где у0 – ордината в конце переходной кривой

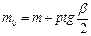7. Расстояние от начала переходной кривой до первоначального положения предельного столбика

8. Полная длина новой кривой (с переходными кривыми):

Lкр=2l0+R(b-2j0).

Суммированный тангенс новой кривой:

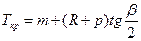Во многих случаях значения m0 и р находят приближенным методом, имея ввиду, что

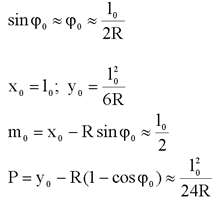
На эксплуатируемых линиях указанный способ применяется, когда сдвижка Р не превышает 25 см.