Уровни энергии и спектры

Уровни энергии атома или молекулы можно получить экспериментально, изучая спектры поглощения или испускания, а также теоретически, решая квантовомеханическую задачу для заданной частицы как многоэлектронной системы. В атомной спектроскопии атом рассматривается как многоэлектронная система, состоящая из неподвижного ядра и движущихся вокруг него в центрально-симметричном поле одного или нескольких электронов. В квантовой механике хорошо разработаны методы решения таких задач, которые позволяют получать значения энергии с необходимой точностью. В настоящее время оба метода, обычно в сочетании друг с другом, находят широкое применение. Рассмотрим решение задачи для простейшего атома водорода, состоящего из одного электрона и протона. Уравнение Шредингера для такой системы имеет вид:

ĤΨ=EΨ,

где Ĥ – оператор энергии, учитывающий кинетическую и потенциальную энергию электронов в поле ядра Ĥ=Т+V; T– оператор кинетической энергии; V– оператор потенциальной энергии. Уравнение (1.1) относительно неизвестных собственных функций Y имеет решение при всех значениях энергии E, а только при некоторых дискретных значениях E₁, E₂, E₃, E₄. Это и есть значения энергии, которыми может обладать рассматриваемая система. Правда, на волновую функцию, Y зависящую от координат (х, y, z) электрона, намечаются условия однозначности, конечности и непрерывности.

Стационарное уравнение Шредингера для электрона в атоме водорода имеет вид

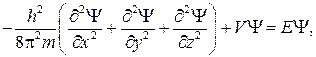
где h – постоянная Планка; m – масса электрона; v – потенциальная энергия; E – полная энергия электрона;

Решив это уравнение, получим дискретный ряд значений энергии

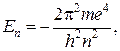
где m – масса электрона; h – постоянная Планка, равная 6,626 × 10^–24;
e – заряд электрона; n – целое число, принимающее значения n = 1, 2, 3, …, ¥. Этот дискретный ряд сходится к границе ионизации атома при
n = ¥ (E_n = 0). При переходе электрона с более высоких уровней энергии (при n = 1) на самый низкий (n = 2, 3, …) получаем линейчатый спектр, соответствующий серии Лаймана, расположенный в ультрафиолетовой области ~ 30000 см^–1.

Следует отметить, что подавляющее число сведений об уровнях энергии атомов и молекул получено экспериментальным путем исследования спектров поглощения и испускания, так как теоретический путь решения задачи для многоэлектронных систем имеет ограниченную применимость. Правда, в последнее время получили широкое распространение полуэмпирические (комбинированные) методы решения многоэлектронных задач, суть которых заключается в том, что во многих случаях конкретных задач находятся приближенные значения энергии и закономерности в расположении их уровней. Постоянные, которые входят в соотношения для значений энергии, определяются из опыта.

Перейдем к классификации уровней энергии молекулярной системы. Рассмотрим сначала отдельную молекулу, состоящую из взаимодействующих между собой атомов. С точки зрения квантовой механики – это многоядерная и многоэлектронная система. Найти уровни энергии такой системы можно только приближенными методами. Наряду с движением электронов здесь необходимо учитывать и движение ядер – колебательное, вращательное и поступательное. Полная энергия молекулы будет состоять из нескольких слагаемых, каждое из которых характеризует свое движение:

E = E_эл + E_кол + E_вр + E_пост+ E_вз ,

где E_пост характеризует поступательную энергию молекулы (как целое), E_вз – энергию взаимодействия между электронной, колебательной и колебательно-вращательной формами движения. Уравнение Шредингера для такой молекулы может быть представлено в виде

(Ĥ_эл+Ĥ_кол+Ĥ_вр+Ĥ_пост+Ĥ_вз)Ψ=EΨ

где Ĥ_эл, Ĥ_кол, Ĥ_вр, Ĥ_пост, Ĥ_вз – операторы энергии, зависящие от координат электронов и ядер, характеризующих каждый вид движения. В энергетическом плане необходимо рассматривать все уровни энергии, соответствующие указанным видам движения. Однако теоретически решить задачу с таким сложным гамильтонианом не представляется возможным. Поэтому в теории надо прибегать к ряду упрощений, чтобы хотя бы приближенно решить задачу о нахождении уровней энергии. Первым упрощением является равенство нулю оператора Н_вз, тогда в уравнении Шредингера можно разделить переменные. Будем пренебрегать энергией поступательного движения молекулы как целого в силу отсутствия дискретного характера энергии в указанном виде движения. Остановимся только на трех основных видах движения в молекуле – электронном, колебательном и вращательном. Всем этим видам движения будут соответствовать свои уровни энергии и соответствующие им спектры (электронные, колебательные и вращательные), а полную энергию молекулы будем представлять в виде суммы

,

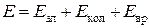Однако движение электронов молекулы, ее колебания и вращения связаны между собой. Поэтому каждое ее стационарное состояние характеризуется как электронно-колебательно-вращательное. Энергетический спектр такой молекулы достаточно сложен и его интерпретация была бы невозможной, если бы не ряд упрощений, которые принимают в теории, если учесть особенности внутренних взаимодействий, обусловленных различием масс электронов и ядер. Это позволяет во многих задачах производить разделение электронного, колебательного и вращательного движений. Возможность разделения всех видов движения в молекуле определяется не только наличием большого числа атомов, но и величиной и спецификой внутримолекулярных взаимодействий, а также степенью перекрытия ее энергетического спектра.

В основе разделения всех видов движения в молекуле на электронное, колебательное и вращательное лежит предположение о медленности движения ядер по сравнению с движением электронов и медленности вращений молекулы как целого по сравнению с колебаниями ядер. Прежде всего это проявляется в значениях частот электронных переходов, которые составляют несколько тысяч см^–1 (30 000 ÷ 15 000 см^–1). Колебательные переходы имеют частоты, на порядок и более отличающиеся от электронных в сторону уменьшения (2000 ÷ 600 см^–1). При квантовомеханическом рассмотрении молекулы обычно пользуются приближением Борна – Оппенгеймера, которое называют адиабатическим.

Оно основывается на различии масс электронов и ядер. Самое легкое ядро атома водорода в 1836 раз тяжелее электрона. Более легкие электроны движутся в молекуле значительно быстрее, чем ядра. За сравнительно малое время, порядка периода колебаний ядер, электроны в молекуле совершают несколько тысяч периодических движений. С точки зрения квантовой механики это будет означать, что фиксированному расположению ядер соответствуют определенные квазистационарные состояния, характеризуемые определенными значениями электронной энергии E_i. В отличие от атома, величина E_i не является строго постоянной, а зависит от расположения (конфигурации) ядер. Волновая функция, описывающая поведение электронов в поле фиксированных ядер, зависит не только от координат электронов, но и от координат ядер как медленно изменяющегося параметра, т. е. Y_эл(r, R), где r означает координаты всех электронов, а R – всех ядер. Уравнение Шредингера для электронов в молекуле запишется в следующей форме:

Ĥ_элΨ_эл(r,R)=E(R)Ψ_эл(r,R),

где оператор Ĥ_эл содержит дифференцирование по координатам электронов, т. е. кинетическую энергию только электронов, а все виды потенциальной энергии являются функцией R. Итак, электронная энергия молекулы не является постоянной характеристикой электронного состояния, а зависит от координат ядер. Графическое изображение этой зависимости называют потенциальной кривой. В случае многоатомной молекулы форма потенциальной кривой (это уже будет многомерная поверхность) достаточно сложна. Обычно при введении нормальных координат их число равно числу колебательных степеней свободы (n = 3 N – 6).

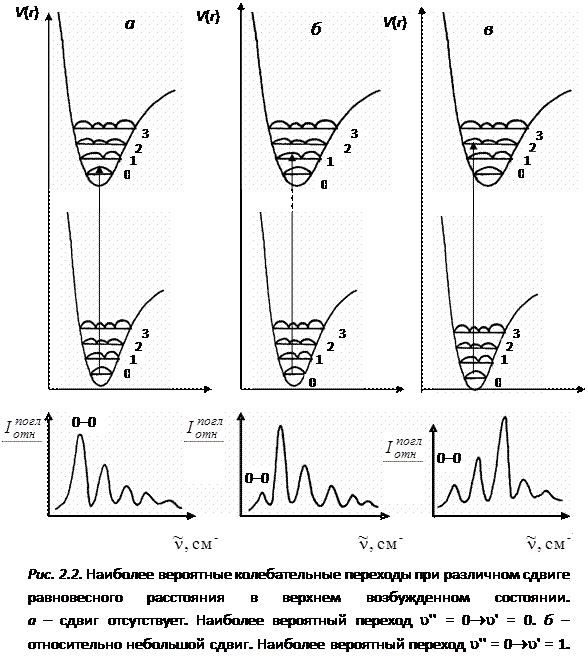
Для двухатомной молекулы имеется только одна колебательная степень свободы, характеризующая расстояние между ядрами, и кривая потенциальной энергии имеет простой вид (рис. 2.1и 2.2). На потенциальных кривых изображены колебательные подуровни нижнего и верхнего электронных состояний. Для простоты приведены только четыре колебательных подуровня. Внизу показан общий характер спектра поглощения двухатомной молекулы. Спектр хорошо передает колебательную структуру двухатомной молекулы, частота колебания которой рассчитывается по формуле классического осциллятора

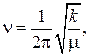
где k – квазиупругая постоянная; m – приведенная масса молекулы.

Наибольшая интенсивность приходится в спектре на полосу соответствующую переходу из нижнего колебательного подуровня u¢¢ = 0 на верхний колебательный подуровень u¢ = 1. Этому переходу соответствует наибольшее перекрытие волновых функций нижнего и верхнего состояний (принцип Франка-Кондона). Это переходы с неизменным межъядерным расстоянием молекулы, происходящие в моменты, когда скорости движения ядер равны нулю. Далее в ультрафиолетовую область интенсивность полос уменьшается практически по экспоненциальному закону.

в силу малости энергии вращательного движения разрешить вращательную структуру колебательных полос можно только с использованием приборов с высокой разрешающей способностью и только для молекул в газовой фазе.

Электронные спектры двухатомной молекулы в газовой фазе представляют собой совокупность полос, отвечающих электронно-колебательным переходам, в которых при высоком разрешении прослеживается вращательная структура. В случае многоатомной молекулы, состоящей из N атомов, колебательная струк­тура отдельной электронной полосы значительно усложняется за счет увеличения числа колебательных

подуровней (рис. 2.3). В нелинейных многоатомных молекулах число колебательных подуровней равно числу колебательных степеней свободы. Отдельные электронно-колебательные полосы могут налагаться друг на друга, что приводит к их перекрытию и уширению. В зависимости от степени усложнения электронно-колебательных спектров все многоатомные молекулы условно подразделяют на простые (в спектре хорошо наблюдается колебательная структура), полусложные (в которых просматриваются следы колебательной структуры) и сложные, в которых полностью утрачивается колебательная структура и электронная полоса представляет собой бесструктурный куполообразный контур. К последним относится большое число органических соединений, широко представленных в природных объектах и имеющих разнообразные практические применения. При наличии в структурах таких молекул систем сопряженных связей (чередующиеся одиночные и двойные связи – C – C = C, ароматические циклы, гетероциклы с включением в кольцо атомов азота, кислорода и др.), а также разнообразных заместителей, включающих карбоксильные, карбонильные, гидроксильные аминогруппы и др., электронные полосы поглощения и испускания этих соединений располагаются в ультрафиолетовой, видимой и ближней ИК-областях, что делает их доступными для экспериментального изучения. С увеличением числа заместителей или сопряженных групп полосы поглощения и испускания обычно сдвигаются в низкочастотную область. Для разрешенных по спину переходов (DS = 0) сечения поглощения составляют величины 10^–18 ÷ 10^–16см², а силы осцилляторов этих переходов находятся в пределах f_осц » 0,1 ÷ 1,0.

На рис. 2.3 приведены уровни энергии сложной молекулы и возможные переходы между ними при поглощении света. Нижние электронные состояния обозначаются S₀ , верхние – S₁. Внизу приведен общий вид спектра поглощения сложной молекулы.

Спектры атомов и двухатомных молекул весьма индивидуальны. Каждой молекуле или атому соответствует свой весьма характерный спектр поглощения и испускания. Спектры сложных молекул также обладают некоторой индивидуальностью. Положение полос поглощения и испускания в шкале частот (или длин волн) различно. Однако эта индивидуальность весьма ограничена, вследствие бесструктурности электронных полос.