Властивостей датчика.

Задача синтезу оптимальної системи фільтрації 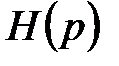і за наявності інерційного датчика може бути вирішена доволі просто інженерними методами теорії автоматичного керування. Використання цих методів вказує по сутності на перехід від ідеальної фільтрації до реальної, по відношенню до якої мається свобода вибору не всієї додаткової функції H(p) оптимальної системи НЧ+ЗЧ, а лише її частини. Іншими совами реальний фільтр має напівжорстку структуру. Тут НЧ — незмінна частина системи (датчик з динамікою Wd), а ЗЧ — активно змінна її частина з допомогою різних корегуючих пристроїв . Засоби вводу цієї аналогової корекції в систему H(p) показані на рис.11.3.

Рисунок 11.3. — Реальний фільтр Вінера.

Викладені передумови дозволяють ставити та вирішувати задачі синтезу реальних фільтрів вимірювальної інформації від некорельованих завад. Коли відомі: статистичні характеристики корисного сигналу та завади; функції H(p) оптимальної системи фільтрації, яка забезпечує виконання вимог точності; динамічні властивості датчика Wd — необхідно знайти таку функцію корегуючого пристрою , яка б забезпечила оптимальність системи фільтрації в цілому.

Вирішення поставленої задачі врахування динамічних властивостей датчиків виходить з рис.11.4:

; ; ,

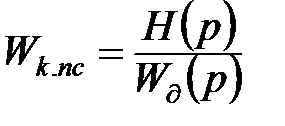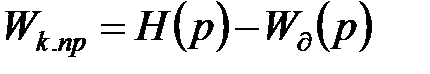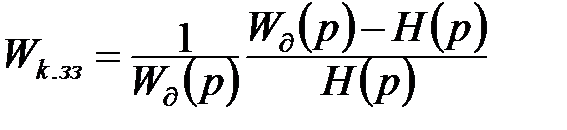де

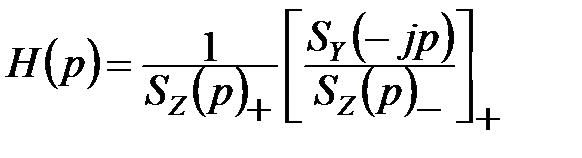. (11.29)

Тут “пс”, “пр”, “зз” — відповідно послідовна, паралельна корекція, а також корекція у вигляді негативного зворотного зв’язку.

Рисунок 11.4. — Види аналогової корекції.

Введення аналогових засобів корекції до системи фільтрації може відбутися трьома способами. При цьому доцільно діяти за наступними рекомендаціями:

1. Використання корегуючого пристрою того чи іншого типу обумовлюється зручністю технічної реалізації.

2. Засоби корекції послідовного типу особливо зручні в тому випадку, коли корисний сигнал є електричний у вигляді постійної напруги. В цьому випадку коригувальні ланки будуються на засадах пасивних контурів, які мають R-, C-, L-елементи.

3. Корекція паралельного типу застосовується, коли до закону фільтрації необхідно додати інтеграли та похідні.

4. Зворотній зв’язок найбільш зручний для корекції, що обумовлюється простотою її технічної реалізації. Негативний зворотній зв’язок зменшує вплив нелінійних зв'язків датчика. Цей вид зв’язку може створювати у динамічному відношенні різні ефекти і, таким чином, деформувати у необхідному напрямку динамічні властивості датчика. Зворотній зв’язок особливо необхідний, коли проявляється нестабільність датчика у часі. Застосування в якості корегуючих засобів негативних зворотних зв’язків дозволяє отримати кращі результати у порівнянні з іншими видами корекції.

На підставі викладених рекомендацій і виразу (11.29) можна зробити такий висновок.

Розрахунковим шляхом найбільш просто знаходити параметри послідовної корекції, а з точки зору сукупності усіх властивостей фільтрації вигідно застосовувати зворотні зв’язки.

У зв’язку з цим представляється доцільним встановити аналогію між зворотнім зв’язком та послідовною корекцією на підставі формули переходу:

.

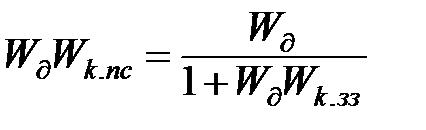Звідки:

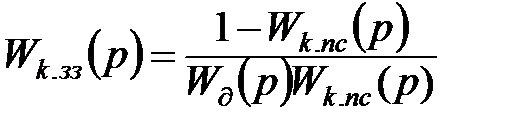, (11.30)

підставивши сюди 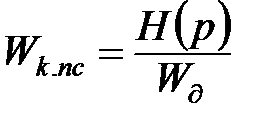, отримаємо:

.

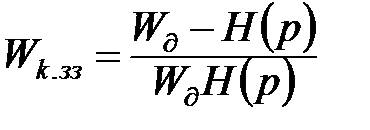Покажемо застосування наявної процедури урахування динамічних властивостей датчика (11.29) – (11.30) на прикладі раніше отриманої оптимальної системи фільтрації (11.32):

.

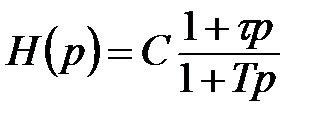Нехай заради конкретності динамічні властивості інерційного датчика описуються аперіодичною ланкою:

,

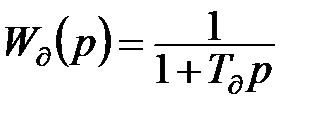де 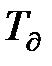— стала часу датчика, а його коефіцієнт передачі прийнятий рівним одиниці, оскільки він впливає тільки на масштаб фільтрованих сигналів.

Використовуючи (11.29) відносно безпосередньо або формулу (11.30) через (11.29) відносно , так чи інакше приходимо до одного і того ж результату — корекції на динамічні властивості датчика у вигляді негативного зворотного зв’язку:

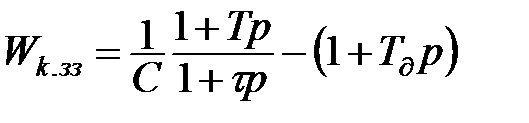. (11.31)

Ця корекція за допомогою інженерних методів теорії керування виражена на рис.11.5. через типові ланки.

Рисунок 11.5. — Реальний фільтр Вінера.

Аналогічні результати можливо отримати при використанні процедури (11.29) – (11.30) до субоптимальних неперервних структур фільтрації. Але найбільший інтерес представляє врахування інерційних властивостей датчика у випадку субоптимальної структури експоненціального згладжування:

.

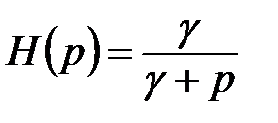Нехай 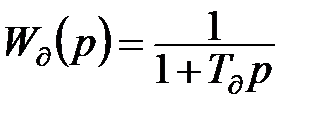, тоді відповідно (11.29) в колах зворотного зв’язку датчика для компенсації інерційності 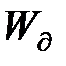повинно бути ввімкнено диференційну ланку:

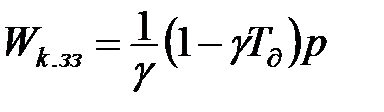(11.32)

створюючи таким чином реальний неперервний фільтр експоненціального згладжування (див. рис.11.6).

Рисунок 11.6. — Реальний неперервний експоненціальний фільтр.

Зворотній зв’язок (11.32) так деформує динаміку датчика, що примушує його працювати одночасно і в якості експоненціального фільтра. Субоптимальність цього реального фільтру забезпечується формулами (11.5) – (11.7), які залишаються справедливими і для розглянутого випадку.

Формула (11.32) показує, що доки 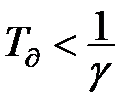зворотний зв’язок залишається негативним і підсилює згладжувальні властивості фільтруючої системи до границь, що визначаються значенням 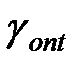. Якщо інерційні властивості датчика такі, що

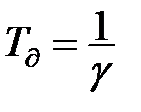, (11.33)

то відповідно (11.32) 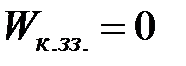і датчик будь якого зворотного зв’язку самостійно здатен одночасно виконувати функції і експоненціального фільтра. При 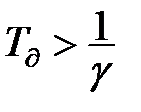зворотній зв’язок перестає бути негативним, вихідний сигнал датчика піддається диференціюванню, захищаючи корисний сигнал від надлишкового згладжування. Так на конкретних прикладах фільтрації проявляються особливі властивості і універсальність зворотного зв’язку.

Разом з тим, зворотний зв’язок, який охоплює сам датчик, вдається використовувати далеко не завжди, особливо в цифрових системах обробки вимірювальної інформації — там, де стає доцільним використання не аналогових, а програмних засобів корекції, де десятки і сотні аналогових пристроїв-датчиків створюють з дискретними фільтруючими системами-алгоритмами і програмами послідовну пару, по якій циркулює інформація в різних формах свого представлення. В цих умовах доводиться ставити і вирішувати дві задачі послідовної корекції:

Задача №1: необхідність послідовної корекції.

Так як на практиці умова (11.33) виконується нечасто, то при наявності десятків і сотень датчиків дуже обов’язковим стає встановлення тієї нижньої границі:

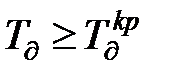, (11.34)

за якою відпадає необхідність в установці спеціального фільтру взагалі. Тут 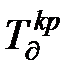— порівняльно мала стала часу датчика, коли сам датчик практично забезпечує фільтрацію завади. Оскільки задача необхідності програмної корекції хоча б на одному з багаточисельних інформаційних каналів вимірювальних систем завжди має позитивне рішення в силу великого різновиду типів датчиків і їх динамічних властивостей, навіть для одного і того ж типу, то постає задача синтезу послідовної корекції.

Задача №2: синтез послідовної корекції.

Сформувати дискретну послідовну корекцію, що має достатні фільтруючі властивості і забезпечує таким чином ефективне фільтрування некорельованих завад, у вигляді програмно-математичних засобів, що реалізуються на ЕОМ. Оптимальність такої фільтруючої системи забезпечується відповідним підбором її структури або, у крайньому випадку, параметрів.

Розглянемо ці дві задачі більш конкретно на прикладі рекомендованого для широкого використання фільтра експоненціального згладжування. По-перше, для вирішення задачі про необхідність корекції утворюємо послідовну пару — інерційний датчик 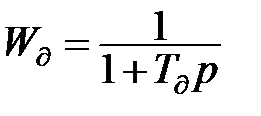і експоненційний фільтр 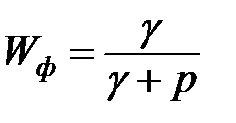(див. мал.11.7). Тоді передаточна функція всієї фільтрувальної системи: 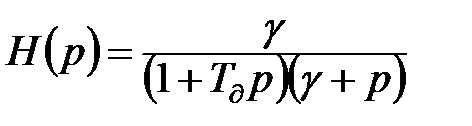, звідки після перетворень і розкладання на елементарні дроби маємо:

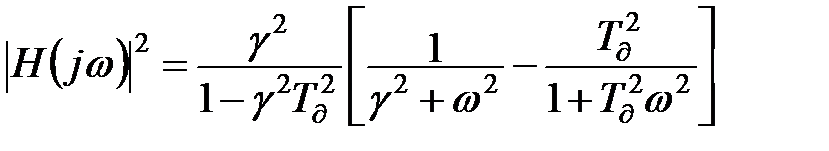; (11.35)

.

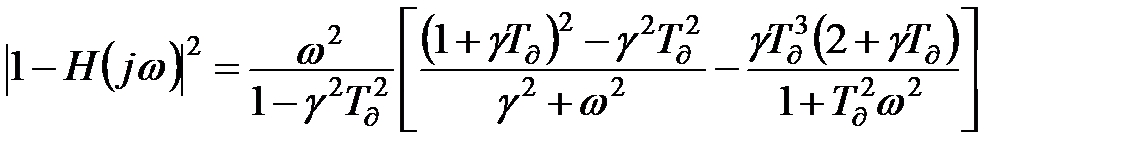Після підстановки виразу (11.35) до формули (11.60) з урахуванням спектральних щільностей входу з (11.1) і взяття неособистих інтегралів, отримаємо вираз для похибки фільтруючої системи , наведеної на рис.11.7.

Рисунок 11.7. — До питання про визначення області використання
експоненціального фільтра.

У неперервному варіанті експоненціального фільтру:

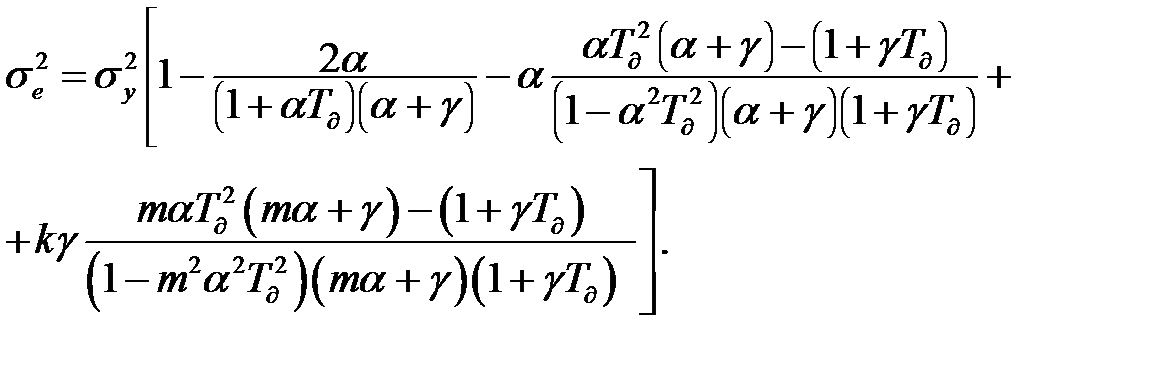(11.36)

яка при 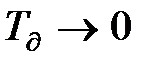вироджується в раніше отриманий вираз (11.5) для безінерційного датчика.

При дискретному варіанті експоненціального фільтру у вигляді (11.10), діючи за процедурою (11.12), (11.13), відповідний вираз для похибки фільтрації має вигляд:

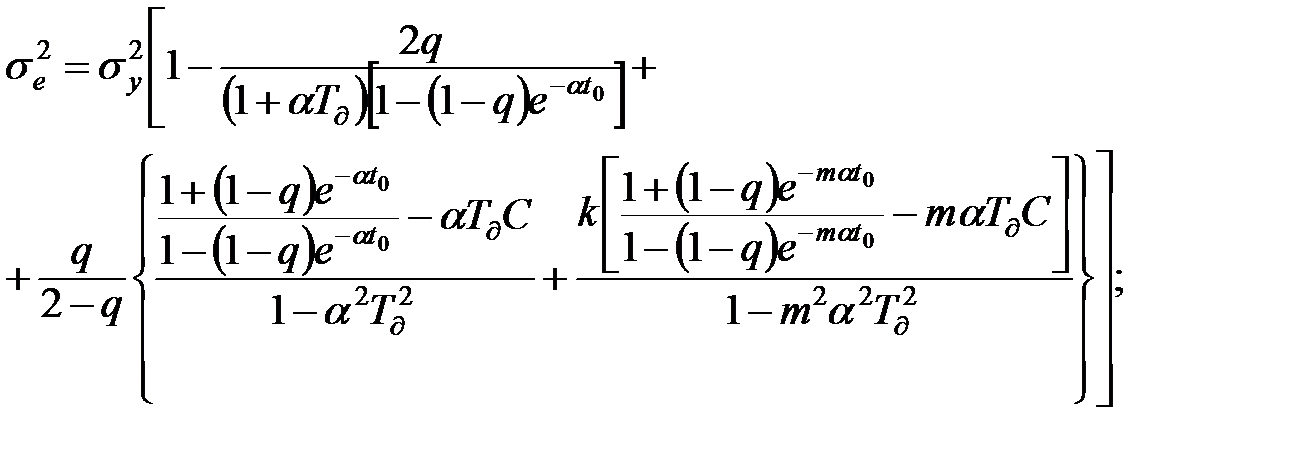
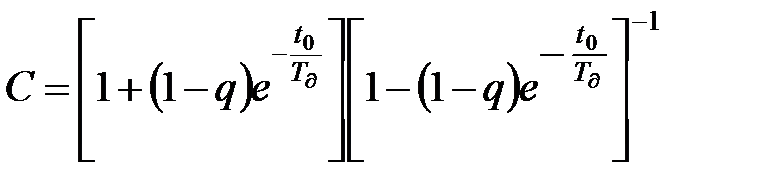, (11.37)

де 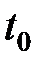— інтервал опитування датчика.

При 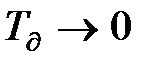вираз (11.36) вироджується у формулу (11.14), яка отримана для безінерційного датчика.

Застосувавши до формул (11.36) і (11.37) класичні чи чисельні методи оптимізації, можливе визначення 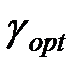і 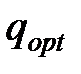в залежності як від характеристик m, α, k вхідного сигналу, так і від інерційних властивостей 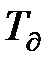датчика та інтервалу його опитування 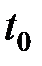. Чисельний аналіз виразів (11.36), (11.37) і порівняння сигналів 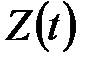і 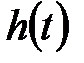, а також похибок 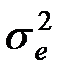з фільтром та без нього, дає область визначення експоненціального згладжування в якості жорстко фіксованої фільтруючої системи при корекції інерційних властивостей датчика по заданим значенням параметрів m, α, k, , .

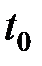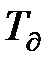В тому випадку, коли на підставі рішення задачі (11.36) чи (11.37) встановлена необхідність в корекції інерційних властивостей датчика до жорстко фіксованої структури експоненціального фільтра (див. рис.11.8), приходиться вирішувати задачу синтезу програмного варіанта послідовної корекції.

Рисунок 11.8. — До питання про синтез корекції, що доповнює інерційність
датчика до структури експоненціального згладжування.

Процедура синтезу базується на (11.29) відносно 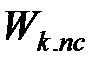і переході в просторі зображень від алгебраїчного рівняння:

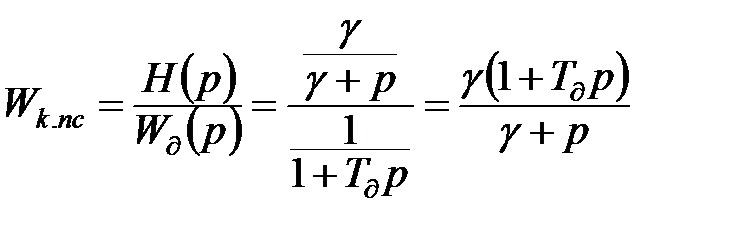; (11.38)

до різницевого: 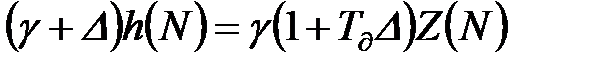, (11.39)

де 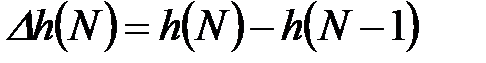і

N — номер такту дискретного часу .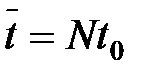

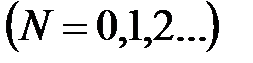Після перетворень з різницевого рівняння (11.39) випливає:

;

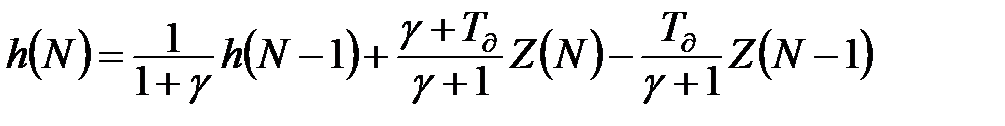чи 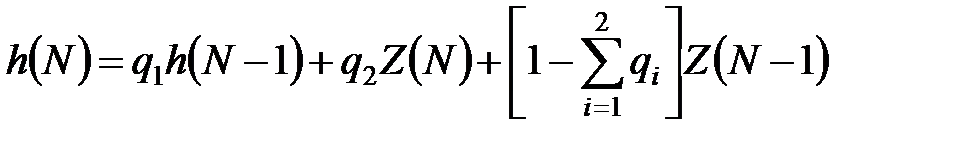, (11.40)

де ; .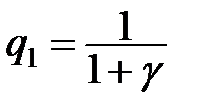

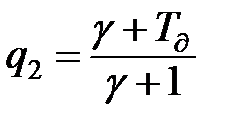Таким чином алгоритм програмної корекції (11.40) являється незміщеним і для своєї реалізації потребує дві комірки пам'яті в ОЗП. Для того, щоб (11.40) був алгоритмом субоптимальним, необхідно доопрацювати його коефіцієнти 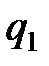і 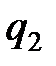або, що теж саме, γ за умови досягнення мінімуму 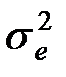. Останнє обумовлюється тим, що якщо найбільший за модулем полюс частотної характеристики:

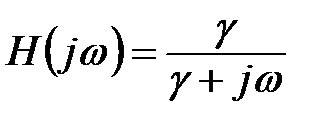
задовольняє нерівності:

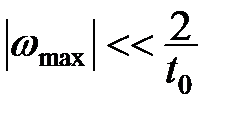, (11.41)

то передаточна функція неперервного варіанту експоненціального фільтру співпадає з його дискретним аналогом і в цьому випадку 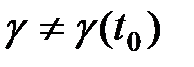і параметр 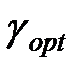визначається з (11.6), в противному випадку 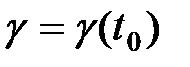і оптимальне значення цього параметру дорівнює:

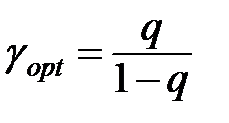, (11.42)

де 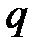знаходиться за формулою (11.16).

Таке можливо собі дозволити, так як дискретизація частини фільтруючої системи до експоненціального згладжування дає менший внесок в похибку фільтрації, ніж дискретизація всієї системи експоненціального згладжування, як це у випадку (11.16).

На закінчення вкажемо на можливість постановки і вирішення за матеріалами цього розділу оптимізаційної задачі вибору того (неперервного чи дискретного) варіанту корекції, який найліпшим чином стикується з конкретним датчиком, або класом датчиків, за критерієм точності або іншим критерієм.

11.4. Суміщення фільтрації та інтерполяції (екстраполяції)

В інженерній практиці досить часто приходиться мати справу з вимірами фізичних величин, зроблених у різні моменти часу. Разом з тим, контроль і аналіз ходу виробничого процесу потребує суміщення результатів вимірювань у часі: одні величини оцінювати у майбутньому (екстраполяція), інші — в минулому (інтерполяція). Наявність завад обумовлює ще й необхідність фільтрації вимірювальних сигналів. При необхідності, як інтерполяція чи екстраполяція вимірюваного значення змінної, так і фільтрації її від завад, ці обидва обчислювальні алгоритми можуть бути суміщені в одній операції.

Теоретичною передумовою такого суміщення операцій служить можливість побудови прогнозуючого фільтра, якщо передаточною функцією вимірювальної системи обрати:

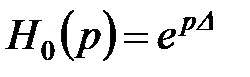, (11.43)

то оптимальна передаточна функція прогнозуючого фільтра за умови фізичної реалізації розраховується відповідно до (11.19).

Так як для прогнозатора: ,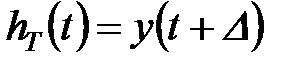

чи ;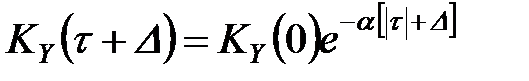

тоді: 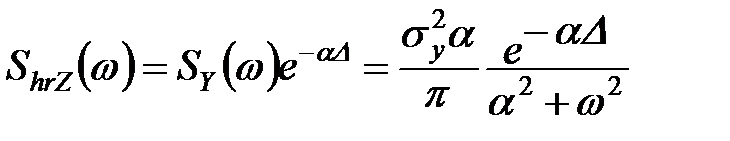. (11.44)

Спираючись на (11.32) кінцево будемо мати:

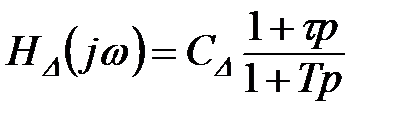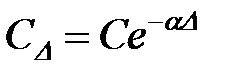; . (11.45)

де параметри С, τ, Т визначені з (11.31).

І, таким чином, коефіцієнт передачі прогнозуючого фільтру С_Δ стає залежним від часового зсуву Δ.

Можна резюмувати: математична постановка сумісної задачі фільтрації з інтерполяцією чи екстраполяцією різниться від задачі для чистої фільтрації лише тим, що в усіх формулах і критеріях замість 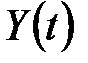представляється 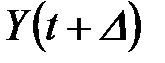. Причому 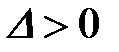для екстраполяції, 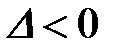для інтерполяції. Більш повно систему прогнозуючої фільтрації розглянемо на прикладі того ж експоненціального згладжування.

Спираючись на (11.43) – (11.45) можна стверджувати, що частотна характеристика прогнозуючого фільтру експоненціального згладжування відповідає:

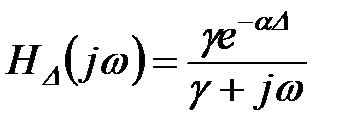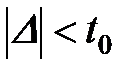; . (11.46)

Похибка такої фільтруючої системи відповідно до (11.60):

.

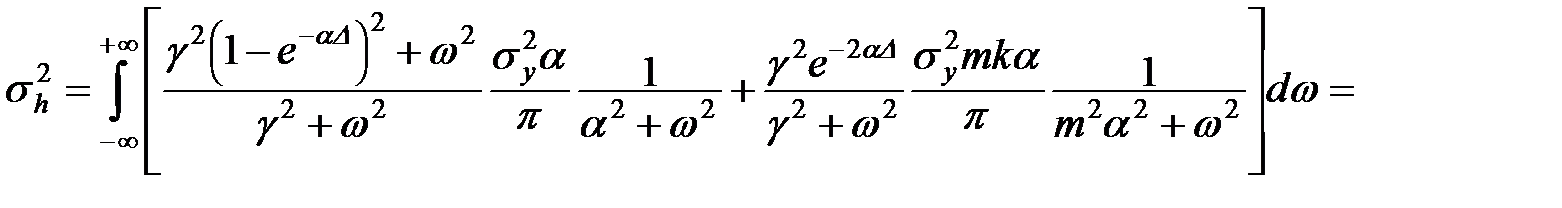
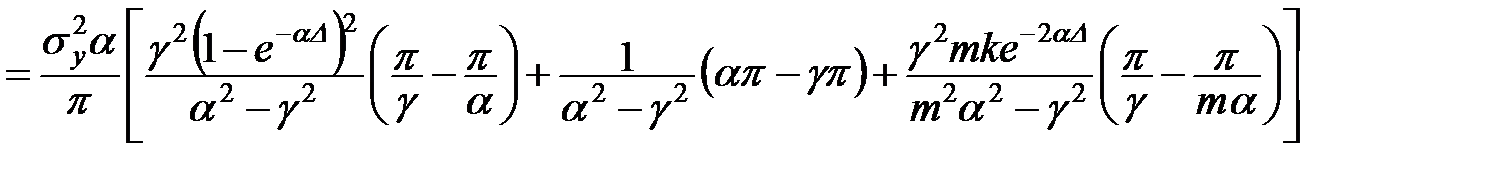Після перетворення:

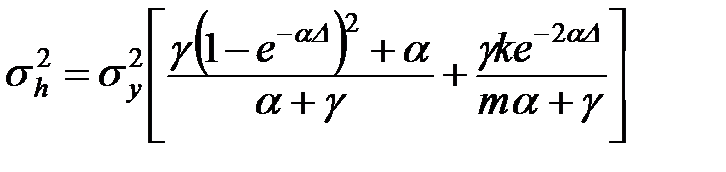, (11.47)

звідки .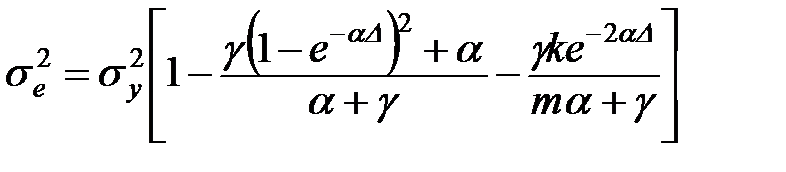

Кінцевий вираз для похибки неперервного варіанту прогнозуючого експоненціального фільтру:

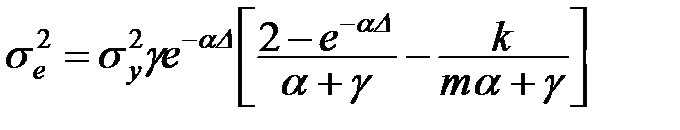. (11.48)

Для того, щоб структура (11.46) стала субоптимальною, необхідно:

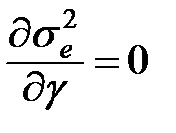і .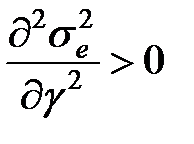

В результаті отримаємо:

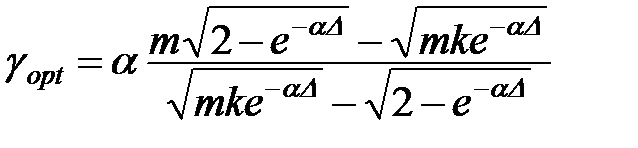. (11.49)

Відмітимо, що раніше отримані результати відносно чистої експоненціальної фільтрації являються лише окремим випадком цієї фільтрації за прогнозом. Справді, виключивши з системи прогноз, 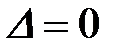, отримаємо відповідні формули.