Застосування експоненційної і стохастичної фільтрації
Основним фактором, що обумовлює практичну придатність того чи іншого фільтра, є чутливість погрішності фільтрації до точності, з якою задані статистичні характеристики корисного сигналу і особливо завади, оскільки остання в реальних умовах відома лише при грубому наближенні. Аналіз цього фактора показує, що чутливість фільтрів до змін параметрів завади в значному діапазоні практично однакова для любих розглянутих вище фільтрів. Однак при грубих оцінках кореляційної функції завади, прості фільтри дають трохи меншу дискретну похибку.
В цілому можна виразити наступні міркування по застосуванню окремих алгоритмів фільтрації.
1. Розповсюджену в практиці вимірювальних систем фільтрацію методом ковзного середнього недоцільно застосовувати ні в неперервному, ні в дискретному варіантах. Вона складна і дає велику похибку, у порівнянні з розглянутими вище більш простими фільтрами.
2. Якщо за характером задач вихідний сигнал 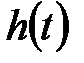 використовується лише у дискретні моменти часу, то необхідно враховувати, що дискретний варіант фільтра майже завжди більш точний і більш простий.
використовується лише у дискретні моменти часу, то необхідно враховувати, що дискретний варіант фільтра майже завжди більш точний і більш простий.
3. У неперервному варіанті доцільно, в більшості практичних випадків, використовувати експоненційний фільтр (11.2) (11.6), так як його легше реалізувати (одноємнісна ланка у вимірювальному колі) і він тільки на 10-30% поступається у якості фільтрації оптимальному статистичному фільтру. Область застосування фільтра експоненціального згладжування досить велика (11.7).
4. У дискретному варіанті при знанні математичного сподівання вимірюваного сигналу з точністю 1–3% стає доцільним застосування зміщеного фільтра першого порядку (11.21) – (11.23), який в значному діапазоні вихідних даних сигналу і завади лише на 5–10% поступається за точністю оптимальному статистичному фільтру. При неточному знанні математичного сподівання корисного сигналу (більше 3%) конкурентними стають між собою алгоритми експоненціального згладжування (11.10), (11.16), (11.17) та незміщеного фільтра першого порядку (11.26) –(11.28). Вони хоча і дають похибку фільтрації, на 30–70% перевищуючи похибку роботи оптимального статистичного фільтра, однак виключно прості у реалізації на ЕОМ, що дуже необхідно при наявності датчиків і сотень вимірювальних в системі контролю і керування змінних, спотворених завадами. Рекурентний алгоритм експоненціального згладжування дає кращі результати, ніж незміщений алгоритм першого порядку. Особливо це видно при значних величинах параметра завади 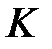 . Для більш детальних практичних рекомендацій по експоненціальному згладжуванню необхідно дослідити роботу рекурентного алгоритму (11.10) з різними виразами для параметра
. Для більш детальних практичних рекомендацій по експоненціальному згладжуванню необхідно дослідити роботу рекурентного алгоритму (11.10) з різними виразами для параметра 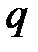 (11.6), (11.16), (11.17) при діапазоні
(11.6), (11.16), (11.17) при діапазоні 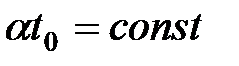 .
.
Дата добавления: 2015-03-03; просмотров: 760;
