Аналогічне відношення для нефорсованої системи

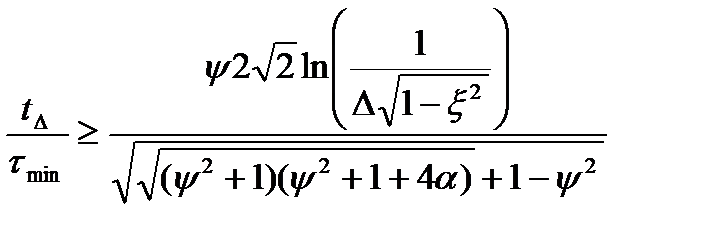. (12.32)

Для умов попереднього прикладу при = 0,05

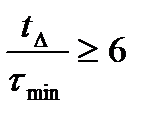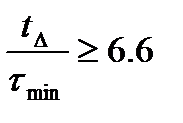, . (12.33)

Якщо відношення дисперсій процесу і перешкоди дорівнює нулю, а амплітуда відносного відхилення дорівнює одиниці, що відповідає умовам приклада, то для форсованої системи можна записати

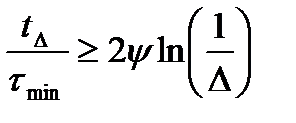(12.34)

Відношення часу асимптотичного настроювання до часу досягнення мінімуму автокореляційної функції пропорційно ступеню затухання випадкового процесу, зокрема, при D=0,05

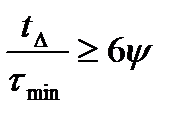. (12.35)

Для умов прикладу, коли α = 5, отримаєм Т_μ= 0,4; τ = 0,9.

Тоді при D = 0,05

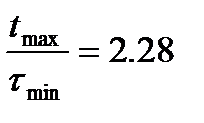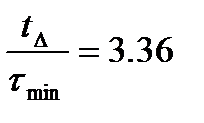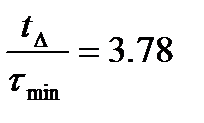; ; (12.36)

Кількість ітерацій n, необхідних для отримання коефіцієнта з

заданою помилкою D, визначається добутком отриманого відношення і відношення q часів досягнення мінімуму автокореляційної функції процесу і зсуву реалізації випадкового процесу, кратного одному вимірюванню q=t_min/t

Тоді:

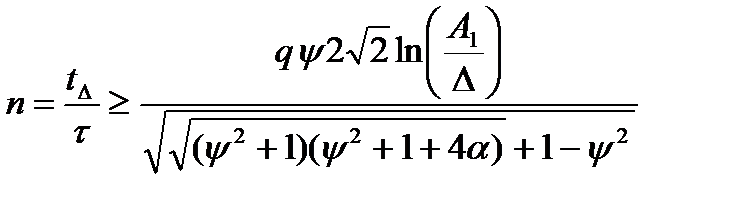(12.38)

Наприклад, якщо t_Λ /t_min ≥ 6, а q =10, то кількість ітерацій n > 10.

Контрольні запитання

1. Назвіть основні методи виконання операцій факторизації і сепарації?

2. У чому полягає фізичне значення ступеня регулярності випадкового процесу?

3. Чим пояснюється критерій мінімуму средньоквадратичної помилки.

4. Назвіть основні параметри перешкодостійкої системи.

5. У яких випадках можна виконати розмикання системи?

6. Чому рівний коефіцієнт передачі замкнутої системи?

7. Пояснити різницю між фізично реалізовуваною і нереалізовуваною системою.

8. Назвати формулу Ван-Тріса, пояснити її фізичне значення.

9. Перерахуйте параметри перешкодостійкої системи.

10. Що називають постійна часу?

11. чому рівний коефіцієнт передачі замкнутої системи.

12. Форсуюча постійна часу, перерегулювання?

13. Як описується передавальна функція для сигналу з періодичної складової і перешкоди у вигляді білого шуму?

14. Як знаходиться передавальна функція прямого ланцюга?

15. Що таке замкнута і розімкнена системи, їх фізичне значення?

16. Що таке зворотний зв'язок і його фізичне значення?