Інженерні методи розрахунку аналогових фільтрів
Проектуючи фільтр, інженер зіштовхується з необхідністю погодження вимог до обробки сигналу з тим, що можна реалізувати наявними засобами. Нерідко буває так, що введення в характеристики фільтра найпростіших обмежень, спрямованих на задоволення поставлених вимог до обробки сигналу, приводить до того, що такий фільтр виявляється фізично нереалізуємий. Рекурсивні, не рекурсивні цифрові фільтри, мінімально фазові, не мінімально фазові, нестійкі фільтри.
Перший етап проектування фільтру – оцінка порогу мінімальної усталеної похибки відтворення сигналу на фоні перешкоди фізично нереалізуємою системою.
Другий етап – апроксимації - побудова стійкої, фізично реалізуємої електронної системи, коли усталена похибка збільшується за рахунок виконання умови фізичної реалізації. В залежності від прийнятого критерію не завжди виконуються умови обмежень, зокрема динамічні показники не задовольняють заданим значенням. Особливо при зростання відносного рівня перешкод та збільшення ступеню регулярності сигналу системи характеризуються підвищеним рівнем коливальності.
Третій етап – корекція динамічних показників для забезпечення гарантованої якості перехідних процесів за допомогою допоміжного критерію, що збільшує усталену похибку.
Такі задачі можна вирішувати в просторі часу, оператор ній формі або з допомогою передавальних функцій або в просторі змінних стану.
Для рішення дуже розповсюдженої інженерної задачі, зв'язаної з розрахунком фільтра, коефіцієнт передачі якого повинний мати задані характеристики в різних частотних діапазонах, маються добре зарекомендували себе методи проектування. Ці методи спираються на ряд стандартних функціональних побудов, що дозволяють реалізувати основні функції фільтрів.
Проектування більшості типів фільтрів починається з їхньої апроксимації у виді фільтра нижніх частот з нормованою ідеалізованою характеристикою. Нормований ідеальний фільтр нижніх частот має одиничний коефіцієнт передачі в смузі частот від 0 до 1 рад/з і нульовий коефіцієнт передачі на всіх частотах, великих 1 рад/с. Фазове зрушення для такого фільтра 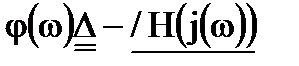 являє собою лінійну функцію, що має одиничний тангенс кута нахилу в смузі пропускання. Для частот, що перевищують 1 рад/з, фазове зрушення не має значення, оскільки на таких частотах фільтр усе рівно не пропускає сигналу. Таким чином, нормований ідеальний фільтр нижніх частот визначається в такий спосіб:
являє собою лінійну функцію, що має одиничний тангенс кута нахилу в смузі пропускання. Для частот, що перевищують 1 рад/з, фазове зрушення не має значення, оскільки на таких частотах фільтр усе рівно не пропускає сигналу. Таким чином, нормований ідеальний фільтр нижніх частот визначається в такий спосіб:
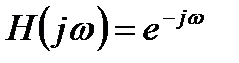 для
для 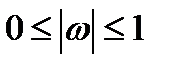 , (8.1)
, (8.1)
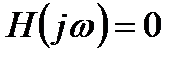 для
для 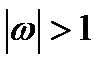 .
.
Модуль коефіцієнта передачі і фазове зрушення обумовлені вираженнями (8.1) зображені на рисунку 8.1.
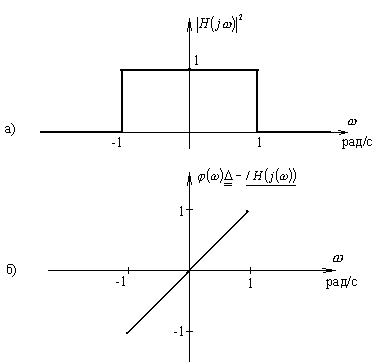
Рисунок 8.1 – Частотні характеристики нормованих ідеальних фільтрів нижніх частот.
Як тільки отримали фільтр нижніх частот з нормованою ідеалізованою характеристикою, відразу ж можна застосувати придатні частотні перетворення за допомогою яких цей базовий фільтр нижніх частот може бути перетворений у фільтр верхніх частот, смуговий, загороджуючий й ін.
Проектування високочастотних, смугових, режекторних фільтрів
на основі низькочастотних. Перетворення спроектованої імпульсної характеристики НЧ фільтра в імпульсну характеристику ВЧ фільтра може бути виконано одним із двох способів.
За методом інверсії спектра знак кожного коефіцієнта фільтра в імпульсної характеристиці НЧ фільтра змінюється на протилежний. Потім до центрального коефіцієнта додається 1.
За методом реверсування спектра змінюється знак кожного другого коефіцієнта. Це приводить до зміни характеристик у частотній області. Іншими словами, якщо частота зрізу НЧ фільтра дорівнює 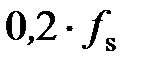 , то результуючий ВЧ фільтр буде мати частоту зрізу
, то результуючий ВЧ фільтр буде мати частоту зрізу 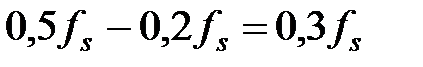 . Це повинно прийматися в увагу при проектуванні вихідного НЧ фільтра. Методи проектування смугових і режекторних фільтрів на основі відомих ФНЧ і ФВЧ наведені на рис. 8.2.
. Це повинно прийматися в увагу при проектуванні вихідного НЧ фільтра. Методи проектування смугових і режекторних фільтрів на основі відомих ФНЧ і ФВЧ наведені на рис. 8.2.

Рисунок 8.2. – Проектування смугових та режекторних фільтрів
з використанням ФНЧ та ФВЧ.
Приклад проектування ВЧ фільтра з використанням імпульсної характеристик НЧ фільтра.
- Метод інверсії спектра:
¨ Проектуємо ФНЧ (лінійна фаза, непарне N).
¨ Змінюємо знак кожного коефіцієнта в імпульсній характеристиці 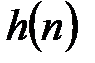 .
.
¨ Додаємо 1 до коефіцієнта в центрі симетрії 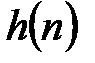 .
.
- Метод реверсування спектра:
¨ Проектуємо ФНЧ;
¨ Змінюємо знак кожного другого коефіцієнта в імпульсній характеристиці 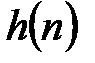 ;
;
¨ Це перевертає характеристику в частотній області ліворуч праворуч Значення по частоті, що відповідає 0, стає відповідним 0,5; 0,5 стає відповідним 0; тобто якщо частота зрізу ФНЧ дорівнює 0,2, то частота зрізу результуючого ФВЧ дорівнює 0,3.
Смуговий і режекторний фільтри можна спроектувати, комбінуючи належним чином відповідні НЧ і ВЧ фільтри. Смугові фільтри проектуються за допомогою каскадного з'єднання НЧ і ВЧ фільтрів. Обчислюючи згортку двох індивідуальних імпульсних характеристик, одержують еквівалентну імпульсну характеристику каскадних фільтрів. Режекторний фільтр проектується за допомогою рівнобіжного підключення НЧ і ВЧ фільтрів і додавання сигналів з їхніх виходів. Складаючи індивідуальні імпульсні характеристики, одержують еквівалентну імпульсну характеристику.
Дата добавления: 2015-03-03; просмотров: 1081;
