Розмикання передатних функцiй форсованих систем
Для реалiзацiї оптимальних i квазiоптимальних передаточних функцiй замкнутих систем виникає необхiднiсть розмикання замкнутої системи.
Оптимальна передаточна функцiя розiмкненої системи для диференцiйовного випадкового процесу має вигляд:
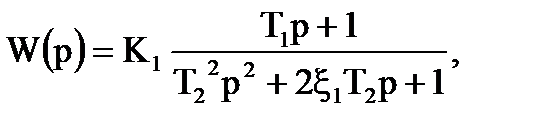 (7.4)
(7.4)
де 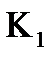 - коефiцiєнт передачi розiмкнутої системи для
- коефiцiєнт передачi розiмкнутої системи для
диференцiйовного випадкового процесу;
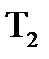 - постiйна часу розiмкнутої системи для диференцiйовного
- постiйна часу розiмкнутої системи для диференцiйовного
процесу;
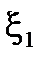 - вiдносний коефiцiєнт затухання розiмкнутої системи для
- вiдносний коефiцiєнт затухання розiмкнутої системи для
диференцiйовного випадкового процесу.
Параметри цiєї функцiї зв'язанi з аналогiчними коефiцiєнтами передаточної функцiї замкнутої системи (Приклад 6) спiввiдношеннями:
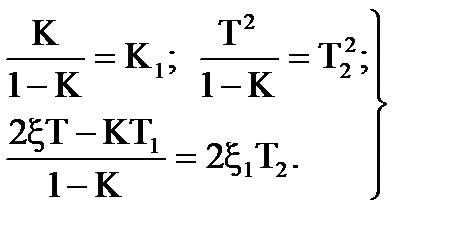 (7.5)
(7.5)
Визначили параметри оптимальної передаточної функції розiмкнутої системи. Коефiцiєнт передачi:
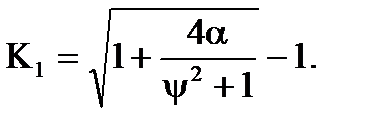 (7.6)
(7.6)
З збiльшенням ступеня регулярностi процесу значення коефiцiєнта передачi зменшується, чим бiльше вiдношення дисперсiй процесу i перешкоди, тим бiльше коефiцiєнт передачi. Добуток постiйної часу функцiї на параметр затухання процесу дорівнює:
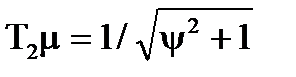 ,
,
i не залежить вiд вiдношення дисперсiй процесу та перешкоди, взятої в смузi процесу, коли α=0. Зi збiльшенням ступеня регулярностi указаний добуток зменшується, якщо ступiнь регулярностi дорiвнює нулю, то добуток постiйної часу на параметр затухання дорiвнює одиницi.
Вiдносний коефiцiєнт затухання розiмкнутої системи дорівнює:
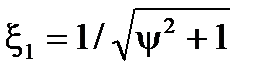 (7.7)
(7.7)
що спiвпадає з попереднiм виразом.
Таблиця 7.1. Структурний синтез оптимальних систем
| № | Спектральна щільність корисного сигналу | Оптимальна структура замкненої системи | Параметри системи | |
| Постійна часу, відносний коефіцієнт затухання | Коефіцієнт передачі | |||
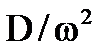
| 1/(Тр+1) | Т=1/α, 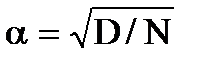
| ||
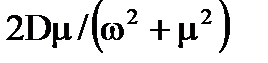
| К/(Тр+1) | 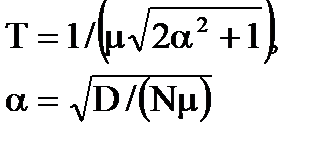
| 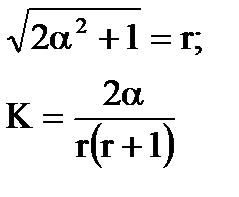
| |
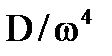
| 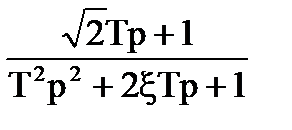
| 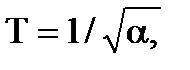 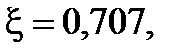
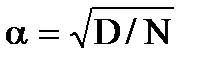
|
Продовження таблиці 7.1
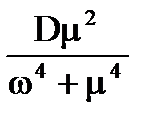
| 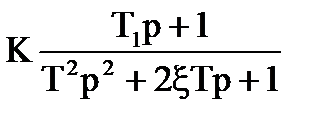
| 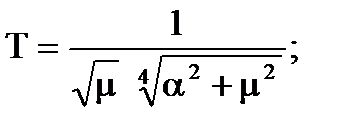 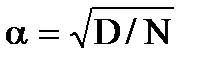 
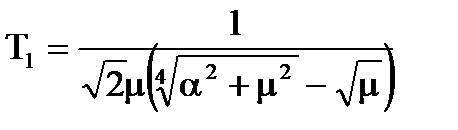
| 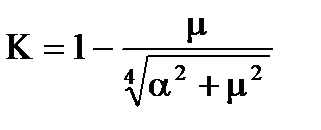
| |
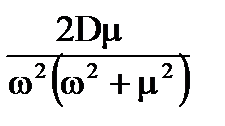
| 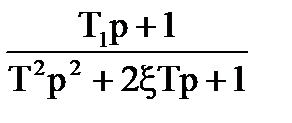
| 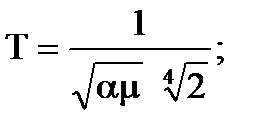 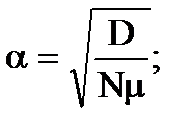 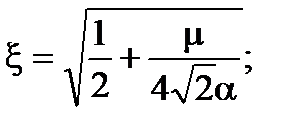 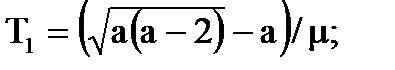 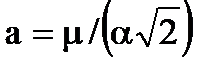
| ||
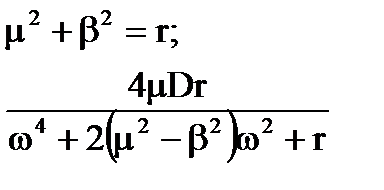
| 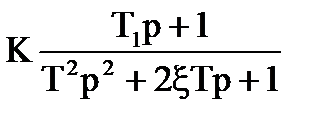
| 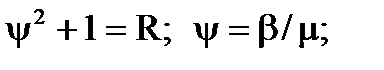 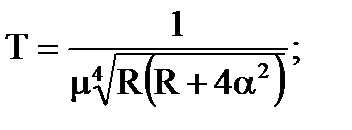 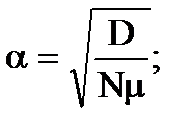 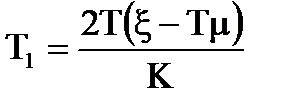 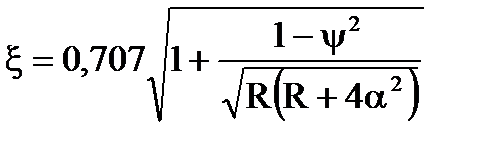
| 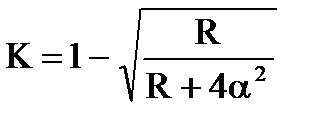
| |
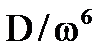
| 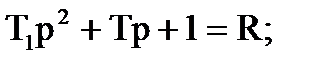
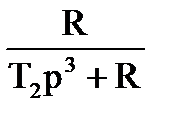
| 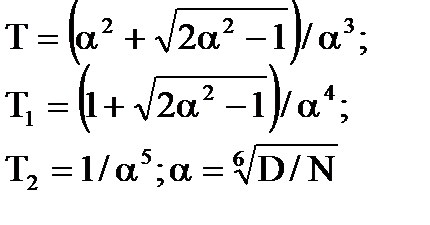
| ||
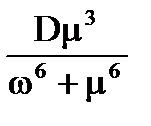
| 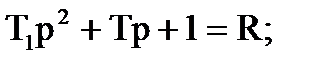
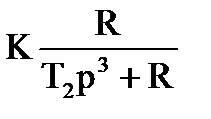
| 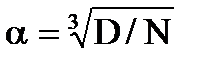 Див. Приклад 8
Див. Приклад 8
| 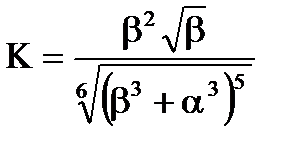
|
Таблиця 7.2. Результати структурного стохастичного синтезу оптимальних систем.
| № | Спектральна щільність корисного сигналу | Корені сигналу в площи ні р | Корені оптимальної передаточної функції (площина р) |
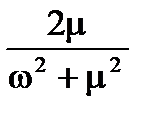
| 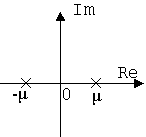
| 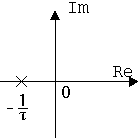
|
Продовження таблиці 7.2
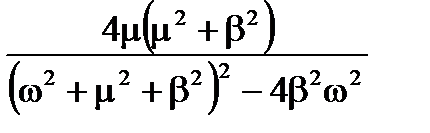
| 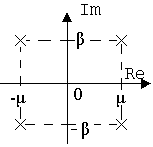
| 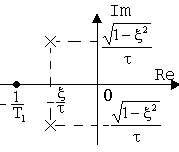
| |
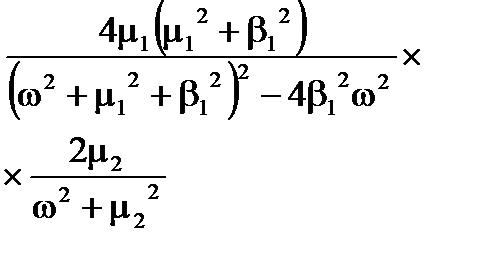
| 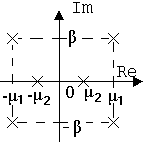
| 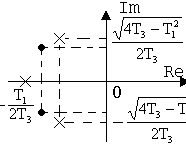
| |
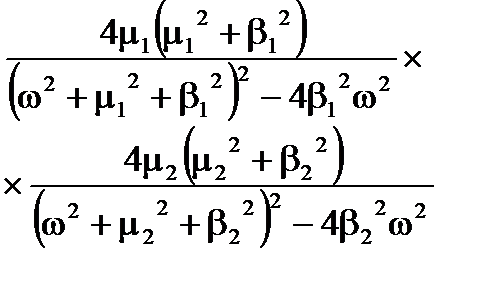
| 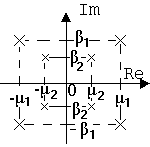
| 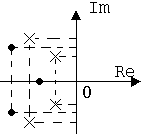
|
Особливiстю постiйної часу i вiдносного коефіцієнта затухання є незалежнiсть вiд вiдношення дисперсiй процесу та перешкоди.
Граничне значення коефiцiєнта передачi замкнутої системи, коли ступiнь регулярностi дорiвнює нулю, а вiдношення дисперсiй процесу i перешкоди - нескiнченностi, дорівнює одиницi. В цьому випадку передаточна функцiя розiмкнутої системи має вигляд:
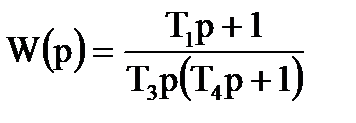 , (7.8)
, (7.8)
де 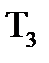 ,
, 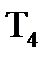 - постiйнi часу.
- постiйнi часу.
Добутки постiйних часу на параметр затухання відповідно дорівнюють:
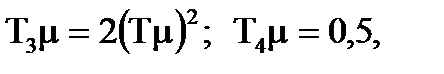
де μ – параметр затухання авто кореляційної функції.
Дослiдження впливу параметрiв випадкового процесу на постiйну часу T3 приведено у главi 3 при розглядi лiнiйних iнтегральних оцiнок якостi, коли К = 1.
Аналогiчно (7.4), запишемо оптимальну передаточну функцiю розiмкнутої системи для недиференцiйовного випадкового процесу (Приклад 7):
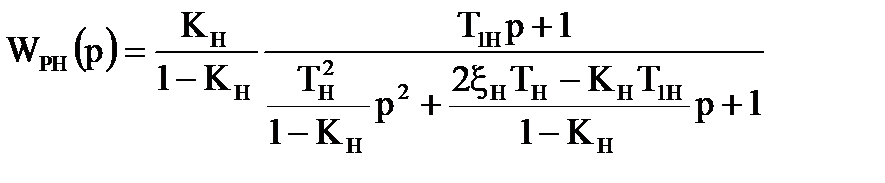 . (7.9)
. (7.9)
В задачi квазiоптимального синтезу параметри функцiї мають вигляд:
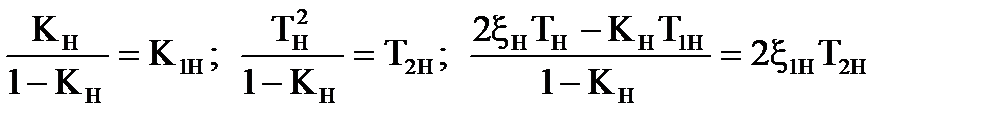 , (7.10)
, (7.10)
де: 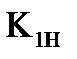 - коефiцiєнт передачi розiмкнутої системи для
- коефiцiєнт передачi розiмкнутої системи для
недиференцiйовного випадкового процесу;
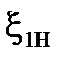 - вiдносний коефiцiєнт затухання розiмкнутої системи.
- вiдносний коефiцiєнт затухання розiмкнутої системи.
Оптимальний коефiцiєнт передачi розiмкнутої системи:
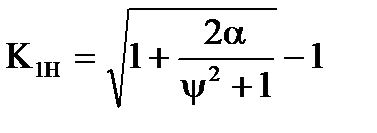 . (7.11)
. (7.11)
Постiйна часу i вiдносний коефiцiєнт передачi спiвпадають з рiвняннями (7.7) і прикладу 7. В задачi оптимального синтезу для недиференцiйовного випадкового процесу параметри визначаються пiдстановкою коефiцiєнта передачi, котрий менший, нiж в задачi квазiоптимального синтезу,особливо з зростанням вiдношення дисперсiй процесу i перешкоди. Тому значення постiйної часу i вiдносного коефiцiєнту затухання збiльшуються .
У вiдповiдностi з передаточною функцiєю оптимальної розiмкненої системи для диференцiйовного процесу в задачах квазiоптимального i оптимального синтезiв та недиференцiйовного процесу у задачi квазiоптимального синтезу (7.4) показник коливальностi при додатних значеннях ступеня регулярностi менше одиницi. Тому динамiчна система являється коливальною.
Постiйна часу T2 i вiдносний коефiцiєнт затухання вiдповiдають аналогiчним параметрам, отриманим для замкнутої системи, коли вiдношення дисперсiй процесу i перешкоди дорiвнює нулю. Параметри характеристичного рiвняння, постiйна часу i вiдносний коефiцiєнт затухання, не залежать вiд вiдношення дисперсiй корисного сигналу i перешкод у смузi процесу.
Характеристичне рiвняння передаточної функцiї розiмкнутої системи має вигляд:
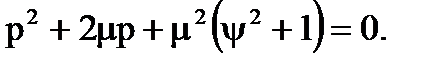
Коренi рiвняння дорiвнюють:
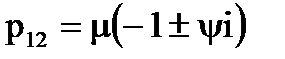 .
.
У випадку, коли 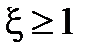 , можливе зпрощення передаточної функцiї регулятора, що можливо переважно для недиференцiйовних випадкових процесiв. Полiном знаменника:
, можливе зпрощення передаточної функцiї регулятора, що можливо переважно для недиференцiйовних випадкових процесiв. Полiном знаменника:
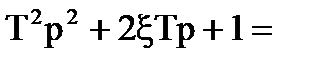
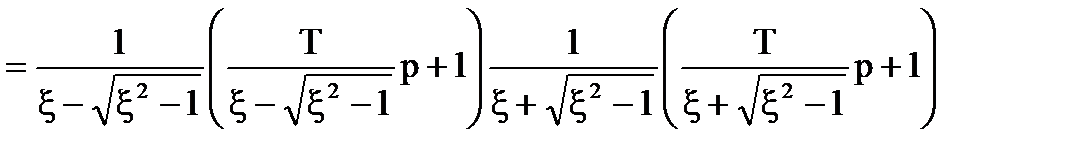 .
.
Зокрема, для недиференцiйовного випадкового процесу:
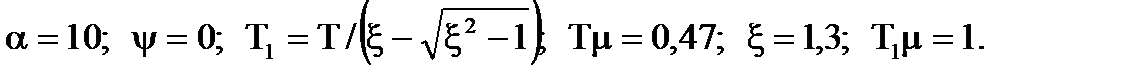
Для реалiзацiї оптимальних рiшень доцiльно розглядати передаточнi функцiї розiмкнутих систем (7.4), коли передаточна функцiя не може бути зпрощена, так як у задачах оптимального i квазiоптимального синтезу для диференцiйовних процесiв та в задачi квазiоптимального синтезу для недиференцiйовних вiдносний коефiцiєнт затухання не може перевищувать одиницi у вiдповiдностi з (7.7). В задачi оптимального синтезу для недиференцiйовних процесiв це можливо.
Розмикання передаточної функцiї замкнутої системи приводить к рiзним передаточним функцiям розiмкнутої системи в залежностi вiд величини коефiцiєнта передачi. Якщо коефiцiєнт передачi замкнутої системи одиничний, то розiмкнута частина являє собою добуток iнтегрувальної та iнтегродиференцiальної ланок. Цього можна досягти, якщо винести пiдсилювальну ланку за межi замкнутого контура.
Якщо коефiцiєнт передачi замкнутої системи менше одиницi, то передавальна функцiя розiмкнутої системи зовнiшньо спiвпадає з (7.11). Коефiцiєнт передачi, постiйна часу i вiдносний коефiцiєнт затухання розiмкнутої динамiчної системи дорiвнюють виразам (7.5) або (7.11).
Використовуючi прийом винесення коефiцiєнта передачi, отримали функцiю розiмкнутого кола (двократне розмикання), зовнiшньо спiвпадаючу з (7.8). Проте, параметри визначаються iз спiввiдношень:
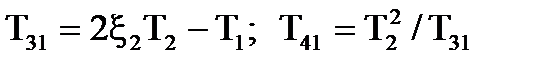 .
.
В iншому виглядi:
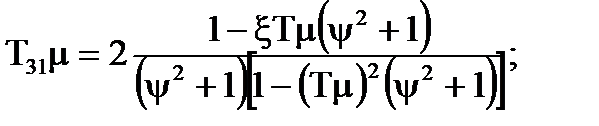 (7.12)
(7.12)
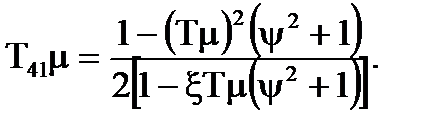 (7.13)
(7.13)
Аналогiчнi параметри при однократному розмиканнi дорiвнюють:
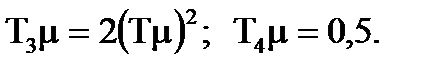
Коли вiдношення дисперсiї процесу i перешкоди дорiвнює нулю, то 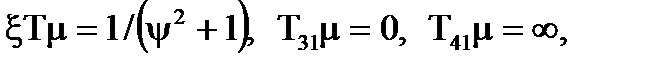 а для замкнутої системи
а для замкнутої системи 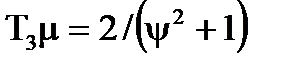 . Коли ступiнь регулярностi процесу дорiвнює нулю, постiйнi часу визначаються спiввiдношеннями:
. Коли ступiнь регулярностi процесу дорiвнює нулю, постiйнi часу визначаються спiввiдношеннями:
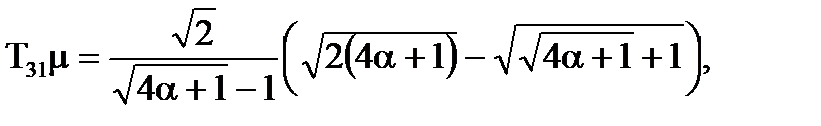
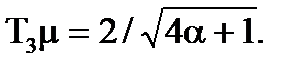
Тодi при α = 0,5 отримали 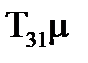 =1,52 i
=1,52 i 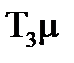 =1,17. Таким чином,
=1,17. Таким чином, 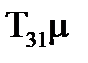 >
> 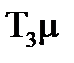 . Постiйнi часу
. Постiйнi часу 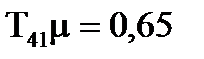 ,
, 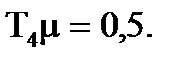 Отже зi збiльшенням значення вiдношення дисперсiї процесу i перешкоди постiйнi часу
Отже зi збiльшенням значення вiдношення дисперсiї процесу i перешкоди постiйнi часу 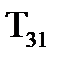 i
i 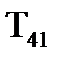 збiльшуються у порiвняннi з
збiльшуються у порiвняннi з 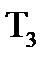 та
та 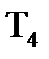 .
.
Розглянемо еквiвалентнi перетворення оптимального рiшення, коли постiйна часу повинна бути значно збiльшена. Квадрат постiйної часу дорiвнює:
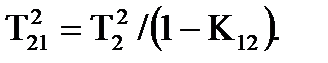
Подвоєний добуток постiйної часу на вiдносний коефiцiєнт затухання:
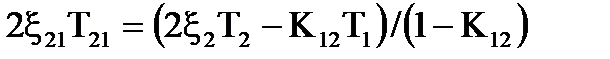 ,
,
звiдки:
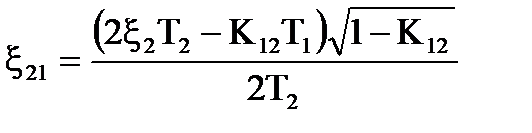 . (7.14)
. (7.14)
При розмиканнi постiйнi часу дорiвнюють:
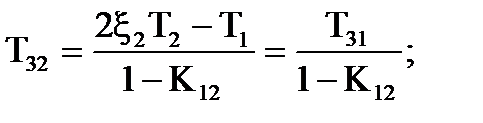
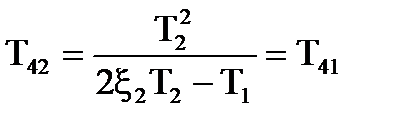 .
.
Таким чином, постiйна часу iнтегрування збiльшується, а 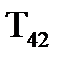 не змiнюється. Коефiцiєнт передачi
не змiнюється. Коефiцiєнт передачi 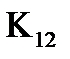 можна вибирати iз умов необхiдного спiввiдношення параметрiв процесу i об'єкту, але не бiльше одиницi. При двократному розмиканнi передаточної функцiї оптимальної динамiчної системи значення коефiцiєнта передачi дорiвнює:
можна вибирати iз умов необхiдного спiввiдношення параметрiв процесу i об'єкту, але не бiльше одиницi. При двократному розмиканнi передаточної функцiї оптимальної динамiчної системи значення коефiцiєнта передачi дорiвнює:
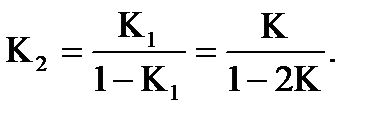
При трикратному розмиканнi:
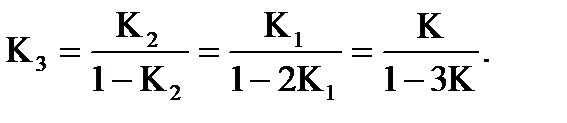
Граничнi значення коефiцiєнтiв передачi для наведених розмикань дорiвнюють:
| однократного | К<1; | 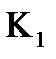 < < 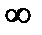 ; ;
| ||
| двократного | К<0,5; | 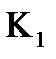 <1; <1;
| 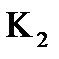 < < 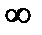 ; ;
| |
| трикратного | К<0,33; | 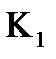 <0,5; <0,5;
| 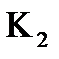 <1; <1;
| 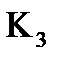 < < 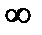 . .
|
В табл. 7.3 наведенi граничнi значення ступеня регулярностi процесу для постiйних вiдношень дисперсiй процесу i перешкоди, вiдповiднi рiзним умовам статистичного синтезу.
Якщо ступiнь регулярностi процесу виявиться менше табличного значення, то реалiзацiя оптимальної системи з заданим числом розмикань неможлива.
Параметри динамiчної системи для умов першого розмикання визначається виразами (7.5).
Для другого розмикання одержали наступнi залежностi. Коефiцiєнт передачi:
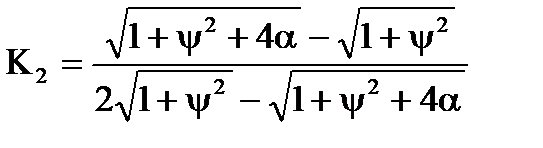 . (7.15)
. (7.15)
Якщо вiдношення дисперсiй процесу i перешкоди дорiвнює нулю, тодi 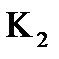 =0. Якщо ступiнь регулярностi дорiвнює нулю, тодi:
=0. Якщо ступiнь регулярностi дорiвнює нулю, тодi:
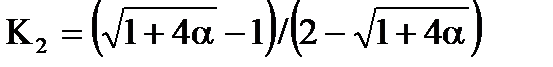 .
.
Умова дотатностi коефiцiєнта досягається тодi, коли 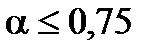 . Квадрат постiйної часу визначається на основi спiввiдношення:
. Квадрат постiйної часу визначається на основi спiввiдношення:
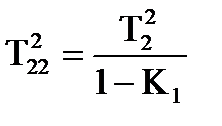 .
.
З урахуванням (7.6) знайдемо добуток постiйної часу на параметр затухання процесу:
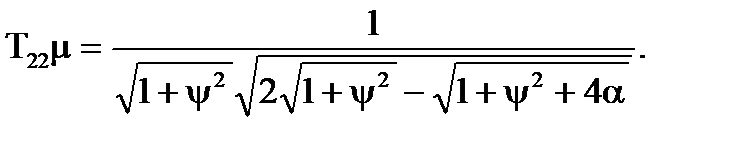 (7.16)
(7.16)
Таблиця 7.3.
Дата добавления: 2015-03-03; просмотров: 871;
