Структура та раціональний порядок елементарної ланки
Передавальна функція в загальному виді представляється відношенням двох багаточленів високого порядку може бути представлена в вигляді суми або добутку елементарних ланок. З алгебри відомо, що поліном довільного ступеня завжди може бути представлений у виді добутку простих множників виду a·s2+b·s+g, причому кожний з коефіцієнтів a, b, g у загальному випадку може дорівнювати нулю. Тому передатна функція електронного пристрою може бути представлена у виді добутку елементарних дробів виду:
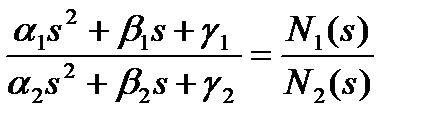 , (7.1)
, (7.1)
причому кожен з коефіцієнтів даного вираження, як було відзначено, також може дорівнювати нулю.
Виникає цікаве запитання як відрізняється реакція пристрою, коли ланка нефорсована, відсутні нулі. Це в повній мірі відповідає класичній теорії автоматичного регулювання. Але навіть в цьому випадку реакція наприклад восьми ланок першого порядку, чотирьох ланок другого порядку, двох ланок четвертого і однієї восьмого дає суттєво різні результати. Але динамічні властивості елементарних ланок другого і четвертого, інколи навіть восьмого порядків можуть бути близькими за заданими за умовами задачі властивостями.
Ситуація ускладнюється при форсуванні елементарних ланок. Білий шум призводить до неповного форсування коли порядок полінома чисельника на одиницю менший порядку полінома знаменника. Оскільки автоматично обмежено перегулювання і коливніть, то виграш може бути ще більший.
Ще більш гострим є питання про реакції в не мінімально-фазових системах – стійких, але з особливими динамічними властивостями.
Таким чином, опис будь-якого електронного пристрою може бути зведений до вираження виду:
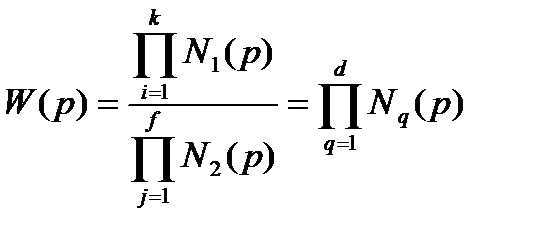 . (7.2)
. (7.2)
Індекси k, f, d вираження (7.2) зв'язані з індексами m і n вихідного диференціального рівняння електронного пристрою співвідношеннями: k ≤ m; d ≤ f ≤ n.
А з вираження (7.2) випливає важливий практичний висновок, що передатну функцію довільного виду можна представити у виді добутку декількох елементарних передатних функцій, причому набір цих функцій згідно (7.1) буде обмежений, тобто функція має стандартний вид. Якщо тепер кожній елементарній передатній функції поставити у відповідність типову ланку, то будь-який електронний пристрій може бути представлений у виді каскадного включення декількох типових ланок.
Аналогічно складна передатна функція може бути представлена в вигляді суми простих елементарних ланок, що відповідає паралельному з’єднанню типових динамічних ланок.
Операція факторизація визначає добуток елементарних ланок. Операція факторизації виконується порівняно просто. Для цього вимагається знайти коріння поліномів спектральної щільності зашумленного сигналу (полюси і нулі) і розкласти поліном на твір простих множників, відповідних лівій (стійкої) напівплощини і правій нестійкій напівплощини параметра Р (або відповідно верхньої і нижньої напівплощин параметра частоти).
Поняття абстрактної алгебри - група кільце та поле.
Група. Групою називають множину або набір елементів, (чисел, багаточленів) об’єднаних одною операцією, умовно називаною як групова операція. Приклади.
Кільце. Множина елементів яка об’єднана двома операціями одна з яких додавання інша множення називається кільцем. Вони бувають комутативними або унітарними. Приклади.
Поле.Полем називається комутативне кільце в якому для кожного не рівного нулю елемента є зворотний відносно прийнятої операції елемент, коли виконання операції дає нейтральний елемент. Ненульові елементи утворюють Авелеву групу за множенням. Це означає, що над елементами поля всі чотири раціональні операції (додавання, віднімання, множення, ділення на ненульові елементи) можуть бути проведені як над звичайними числами. Для полів залишаються в силі всі правила елементарної алгебри. Приклади.
Питання раціональної структури елементарної ланки залежить від поставленої задачі.
Статистичною характеристикою елементу системи або системи в цілому називається залежність вихідної величини хвих від вхідної величини хвх в положенні рівноваги:
хвих=f(хвх) (7.3)
Якщо залежність представлена лінійною функцією хвих=хвх0+kхвх, де k=tga, то характеристику і елемент (ланка) називають лінійним, тут k – коефіцієнт передачі, розмірність якого: одиниці вихідної величини, ділені на одиниці вхідної величина. У всіх інших випадках характеристику і елемент називають нелінійним.
У більшості випадків статичні характеристики нелінійні.
У загальному випадку за наявності вихідних величин динаміка елементу (ланки) системи описується нелінійним диференціальним рівнянням
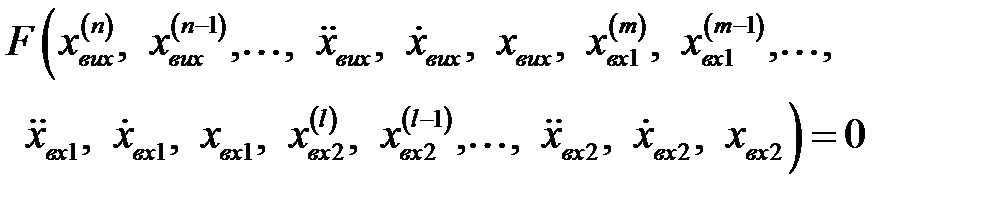
Приклад.Вивести диференціальне рівняння. Елемент (наприклад ланка із зворотним зв'язком) є пасивним чотириполюсником (мал.7.1). Вхідна величина – напруга на лівих клемах, вихідна – напруга на правих клемах.

Мал. 7.1. – Схема елементу.
На основі закону Кирхгофа запишемо
Uвх=UR1+UR2+UC2
UC1=UR2+UC2;
i=i1+i2
де UR1, UR2, UC2, UC1=Uвих – падіння напруги на відповідному резисторі або місткості. Використовуючи закон електротехніки:

Проводячи підстановки в основі управління і перетворюючи їх одержимо:
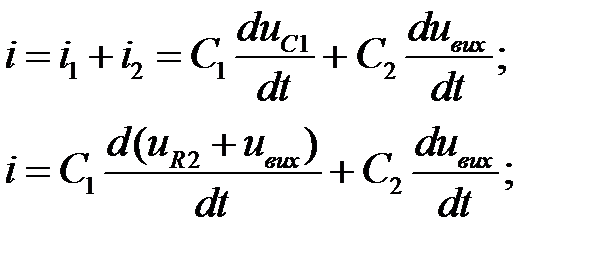
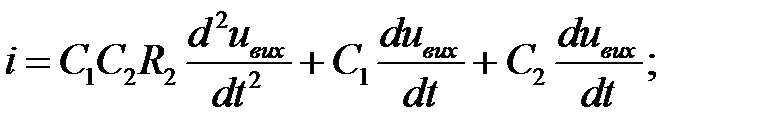
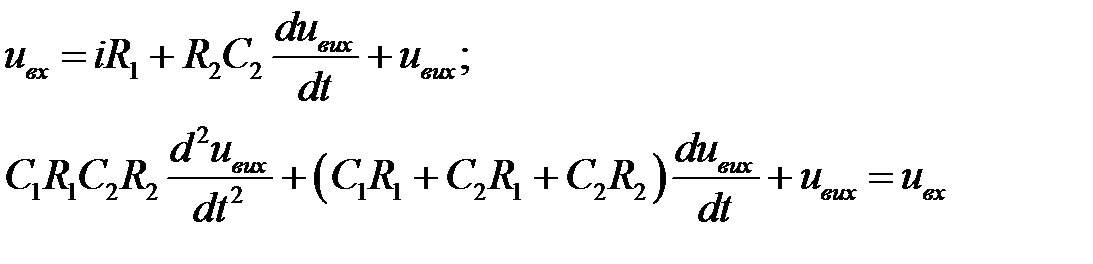
У загальному вигляді можна записати;
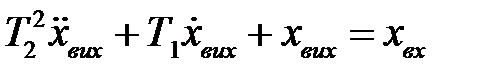 ,
,
де 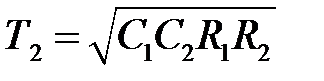 і Т1=С1R1+С2R1+C2R2 – постійні часу.
і Т1=С1R1+С2R1+C2R2 – постійні часу.
Дата добавления: 2015-03-03; просмотров: 911;
