Усталену похибку системи

Дисперсія помилки електронної системи може розглядатися як деякий функцiонал:

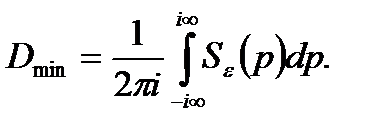(6.1)

Оптимальна перешкодостійка система найкращим чином вiдтворює корисний сигнал та в певній мірi придушує вплив неконтрольованих збурень. Функцiонал, який характеризує усталену динамiчну помилку, має мiнiмум. Фiзичний змiст оптимального перетворення суми корисного сигналу та перешкоди мiститься в рiвняннi складових помилки вiдтворення перешкод та неповного вiдтворення корисного сигналу.

Спектральна щiльнiсть помилки:

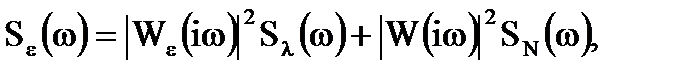
де 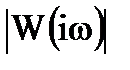та 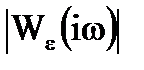- модулi амплiтудно-фазових частотних

характеристик замкнутої системи та вiдносної помилки.

Оптимальнi значення постiйних часу та вiдносних коефiцiєнтiв затухання забеспечують мiнiмiзацiю дисперсiй помилок в сталому режимi. Наприклад, для умов, приведених в таблицi 2.1, рядок 1, оптимальне значення постiйної часу Т= 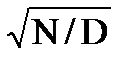забеспечує мiнiмум вiдносної величини усталеної помилки, яка має вид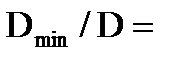 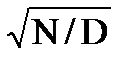. Чим вище вiдносний рiвень перешкод, тим бiльше постiйна часу та величина вiдносної залишкової дисперсiї. Пердаточна функцiя вiдносної помилки для функцiй прикладів 6.1 та 6.2 додатку 1 має вигляд:

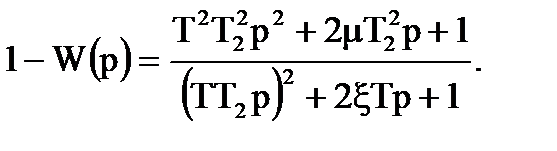(6.2)

Мiнiмальне значення усталеної помилки з врахуванням (6.1) визначається виразом:

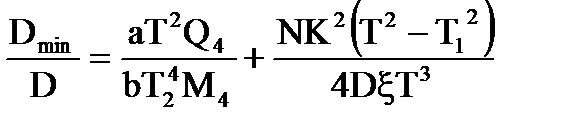, (6.3)

а параметри М₄, Q₄ – характеризуються визначниками:

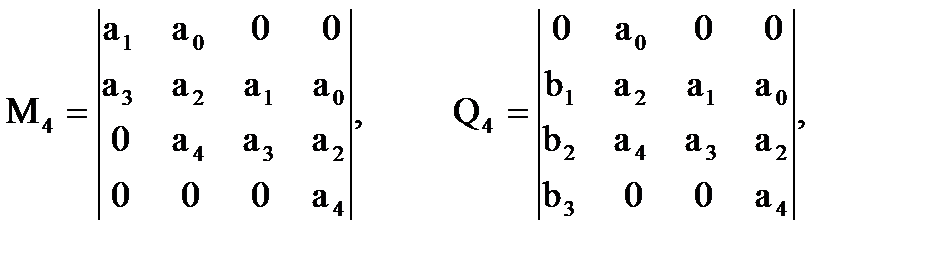(6.4)

де

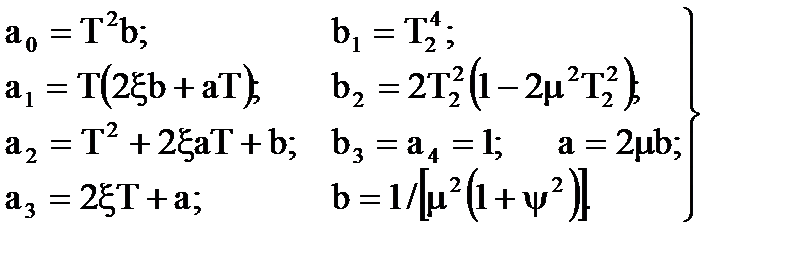(6.5)

Розкриваючи визначники, отримаєм вiдносну величину дисперсiї у задачi квазiоптимального синтезу для диференцiйовного та недиференцiйовного випадкових процесiв:

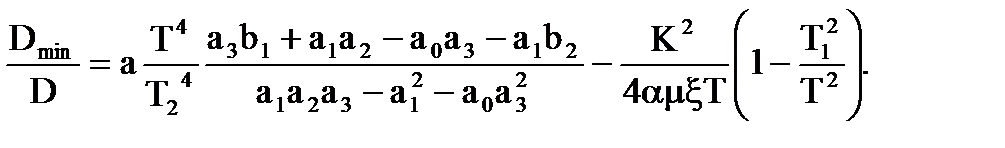(6.6)

Пiдставляючи значення параметрiв, запишемо:

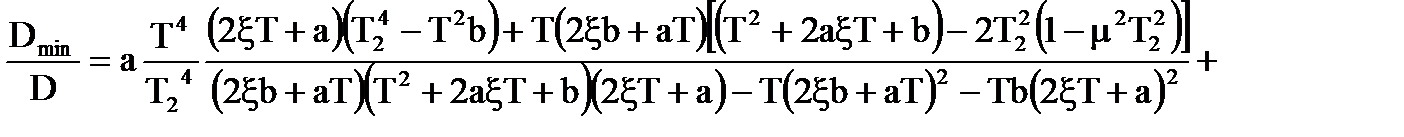
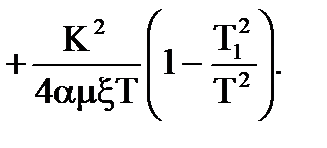(6.7)

В задачі оптимального синтезу для диференцiйовного випадкового процесу вiдносна величина дисперсiї перешкодозахищеної системи має вигляд:

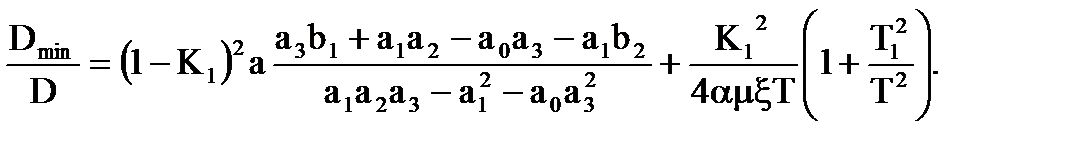(6.8)

Аналогiчна формула використовується для розрахунку вiдносної величини дисперсiї системи для недиференцiйовного процесу. Чим нижче вiдносний вплив перешкод, тим менше величина вiдносної помилки. Абсолютне значення резонансної частоти та швидкостi затухання не впливає на величину вiдносної помилки, а впливає тiльки їх вiдношення. Таким чином, усталена помилка синтезованої за критерiєм мiнiмуму середньоквадратичної помилки динамiчної системи тим менше, чим менше значення вiдносного рiвня перешкод, визначаємого коефiцiєнтом α.

Якщо розглянути залежностi вiдносної усталеної середньоквадратичної помилки вiд ступеня регулярностi диференцiйовного процесу при постiйному вiдношеннi дисперсiй процесу та перешкоди, то цi залежностi в задачах квазiоптимального та оптимального синтезу спiвпадають. Чим бiльше ступiнь регулярностi процесу i менше вiдношення дисперсiй процесу та перешкоди, тим бiльше вiдносна величина помилки, граничне значення якої дорiвнює одиницi.

Найменша вiдносна усталена середньоквадратична помилка спостерiгається для диференцiйовного випадкового процесу.

Оптимальний статистичний синтез САК при довiльнiй структурi для диференцiйовних процесiв приводить до максимальної усталеної помилки:

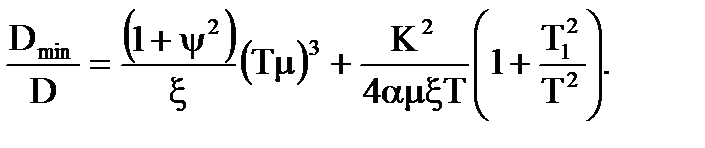, (6.9)

коли складовi дисперсiй не вирiвнюються, що посилюється зi збiльшенням вiдносного рiвня перешкод. Причому складова вiд неповного вiдтворення корисного сигналу бiльше, нiж складова вiд вiдтворення перешкод, що свідчить про недостатню швидкодiю, малий коефiцiєнт передачi та мале значення постiйної часу форсування.