Показникiв якостi динамічних систем

Враховуючi, що добуток часу регулювання на параметр затухання має мiнiмум, визначили спiввiдношення мiж безрозмiрними параметрами вхiдних випадкових процесiв, якi забеспечують вказану умову. Умова мiнiмуму добутку часу регулювання на параметр затухання для диференцiйовної функцiї вiдповiдає бiльшим значенням ступеня регулярностi, чим для недиференцiйовної.

На основi наведених громізких формул доцільно збудувати номограми областей постiйних значень вiдносної середньоквадратичної помилки i показника коливальностi в залежностi вiд безрозмiрних параметрiв вхiдних процесiв. При цьому зi збiльшенням ступеня регулярностi процесу при постiйному значеннi вiдношення дисперсiй сигнала i перешкоди вiдносна середньоквадратична помилка i показник коливальностi збiльшуються

Аналогiчнi номограми для постiйних значень коливальностi, перерегулювання, добутку часу регулювання на параметр затухання i вiдносної усталеної середньоквадратичної помилки в залежностi вiд ступеня регулярностi процесу i вiдношення дисперсiй процесу i перешкоди. Добуток часу регулювання на параметр затухання зменшується як зi збiльшенням ступеня регулярностi при постiйному вiдношеннi дисперсiй процесу i перешкоди, так i з збiльшенням вiдношення дисперсiй процесу i перешкоди при постiйному ступенi регулярностi процесу.

Використовуючi номограми, можна визначити напрям мiнiмального приросту вiдносної помилки. Вiдношення приростiв вхiдних безрозмiрних параметрiв процесiв визначається наступним чином.

Iз рiвняння (6.89) отримали вiдносну середньоквадратичну помилку у виглядi:

;

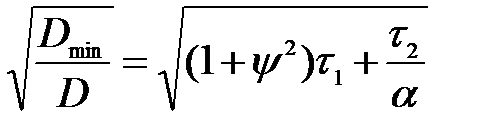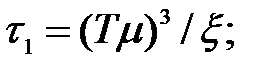
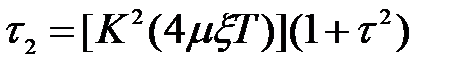Визначили прирiст вiдносної дисперсiї при приростi ступеня регулярностi процесу i вiдношення дисперсiй процесу i перешкоди у виглядi:

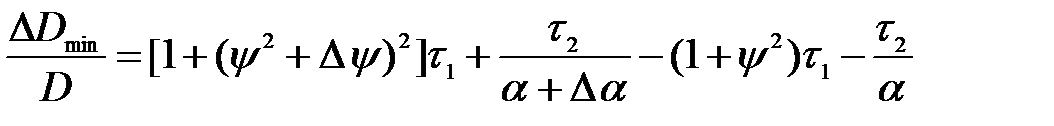абo:

;

де 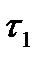, – допомiжнi безрозмiрнi параметри;

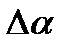– прирiст вiдношення дисперсiї процесу i перешкоди;

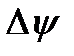– прирiст ступеня регулярностi процесу.

Прирiст обертається на нуль, якщо:

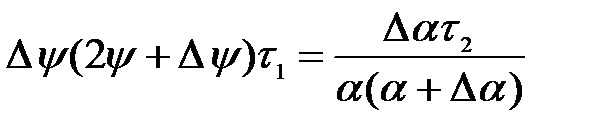Звiдси вiдношення приростiв вiдношення дисперсiй процесу i перешкоди до ступеня регулярностi процесу в першому наближеннi дорiвнює:

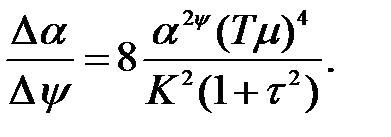
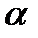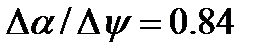Наприклад, при =4 i =3 (точка О) вiдношення . У заданiй точцi пiд кутом до осi абсцис, який визначається як обернена функцiя тангенсу отриманого числа, тобто r=40, проводиться промiнь . Доцiльно прямувати до збiльшення вiдношення дисперсiй процесу i перешкоди, а також до зменшення ступеня регулярностi процесу. Зі збiльшенням вiдношення дисперсiй процесу i перешкоди зменшується як усталена помилка, так i перерегулювання. Для динамiчних систем, одержаних для недиференцiйовного випадкового процесу, умова рiвностi усталеної середньоквадратичної помилки i перерегулювання зміщується в область більших значень ступеня регулярності процесу.