Проверка на нормальность распределения анализируемых данных

Оценить соответствие анализируемых данных нормальному закону можно с помощью модуля «Statistics/Distribution fitting». В диалоговом окне этого модуля (рис.5.6) в списке непрерывных распределений (Continuous Distributions) указывается тип распределения (Normal).

Рисунок 5.6. Диалоговое окно «Distribution fitting»

По нажатию кнопки «OK» будет отображено диалоговое окно настройки процесса оценки нормальности «Fitting Continuous Distributions» (рис.5.7), где по кнопке «Variable» следует выбрать переменные для анализа (например, ID_UNEMPLAYMENT – индекс уровня безработицы).

Рисунок 5.7. Диалоговое окно «Fitting Continuous Distributions»

Нажав кнопку «Plot of observed and expected distributions» (График наблюдаемого и ожидаемого распределений), получим гистограмму распределения данных о индексе уровня безработицы и красную кривую, соответствующую ожидаемому нормальному распределению (у этого ожидаемого распределения те же средняя арифметическая и стандартное отклонение, что и в анализируемой совокупности данных) (рис.5.8). Глядя на полученный рисунок, можно сказать, что в целом распределение значений индекса уровня безработицы соответствует нормальному. Это заключение, основанное на визуальном анализе распределения, имеет и более строгое подтверждение в виде результатов теста 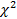(Chi-square test, см. в верхней части графика на рис.5.8). В данном случае этот тест проверяет нулевую гипотезу о том, что наблюдаемое распределение анализируемого признака не отличается от теоретически ожидаемого нормального распределения. Поскольку вероятность ошибиться, отклонив эту гипотезу оказалась больше 0,05 (Р = 0,29541), мы принимаем, что гипотеза действительно верна. Иными словами, распределение значений индекса уровня безработицы статистически не отличается от нормального распределения.

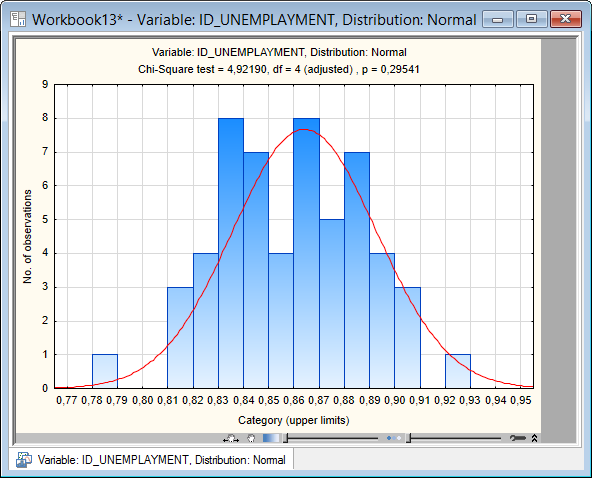
Рисунок 5.8. Гистограмма распределения значений индекса уровня безработицы и ожидаемая нормальная кривая

5.2.3. Тесты Колмогорова – Смирнова и Шапиро – Уилка

Следует отметить, что мощность теста 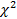при проверке нормальности распределения анализируемых данных относительно невысока (другими словами, его применение достаточно часто приводит к ошибочному выводу о нормальности распределения). Поэтому лучше воспользоваться и другими тестами. Их можно найти в уже рассмотренном выше модуле «Descriptive Statistics». После запуска этого модуля необходимо открыть закладку «Normality» и в поле «Distribution» (Распределение) разыскать опции «Kolmogorov-Smirnov and Lilliefors test for normality» (Тест Колмогорова-Смирнова и Лиллифорса на нормальность) и «Shapiro-Wilk’s W test» (W-тест Шапиро-Уилка). Равно как и критерий 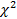, эти тесты проверяют нулевую гипотезу об отсутствии различий между наблюдаемым распределением фактора и теоретическим ожидаемым нормальным распределением. Наиболее предпочтительным, особенно при небольших выборках (N = 3 ÷ 50) является использование W- критерия Шапиро-Уилка, поскольку он обладает наибольшей мощностью в сравнении со всеми перечисленными критериями (т.е. чаще выявляет различия между распределениями в тех случаях, когда они действительно есть). Для выбора того или иного теста, достаточно поставить флажок рядом с его названием. После выбора анализируемой переменной (кнопка «Variables») и нажатия кнопки «Histograms» программа создаст гистограмму распределения значений фактора и ожидаемую нормальную кривую (рис.5.9). Результаты выбранных тестов на нормальность автоматически располагаются в заголовке этого графика. При Р > 0,05 можно заключить, что анализируемое распределение не отличается от нормального. В примере с данными об индексе уровня безработицы для теста Шапиро-Уилка получаем Р = 0,45749 (рис.5.9), что подтверждает сделанный ранее вывод о нормальности распределения этих данных.

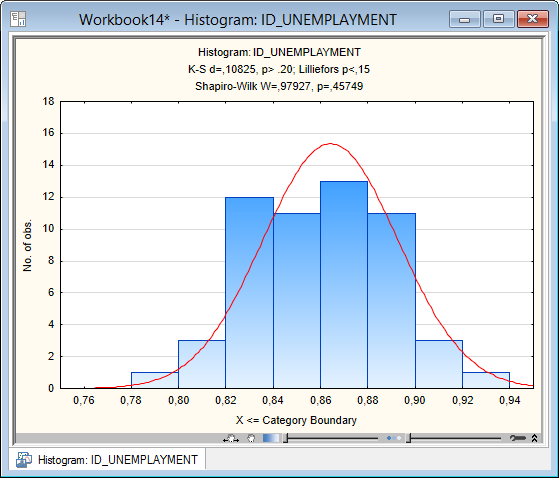
Рисунок 5.9 Гистограмма распределения значений индекса уровня безработицы и ожидаемая нормальная кривая по критерию Колмогорова-Смирнова и Шапиро-Уилка