Анализ Результатов Серии Экспериментов
После завершения серии экспериментов выводится диалоговая форма с результатами серии. Она содержит 3 вкладки:
1. Общая информация.
2. Таблица результатов.
3. Графики результатов.
3.9.3.1.Вкладка «Общая информация».
Данная вкладка высвечивается сразу по открытию результатов серии экспериментов.
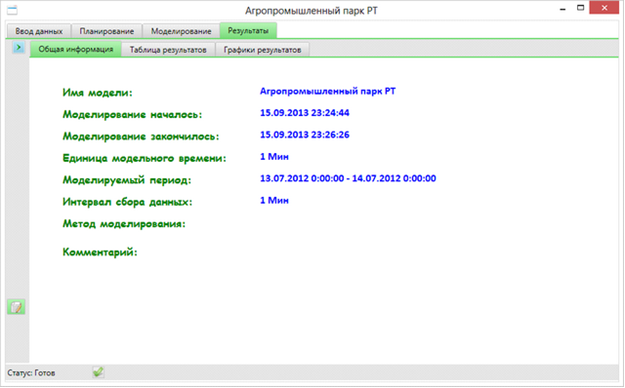
Рисунок 3.64. Вкладка «Общая информация» серии экспериментов
Вкладка содержит общее описание результата моделирования: наименование модели и серии экспериментов, время фактического начала и завершения серии экспериментов, единица модельного времени, моделируемый период, метод планирования экспериментов.
3.9.3.2.Вкладка «Таблица результатов».
Данная вкладка отображает таблицу, в которой выведен план серии и все целевые показатели. Каждая строка – это один эксперимент. Сначала выводятся заданные в конкретном эксперименте значения факторов, а затем, полученные в результате моделирования показатели модели.
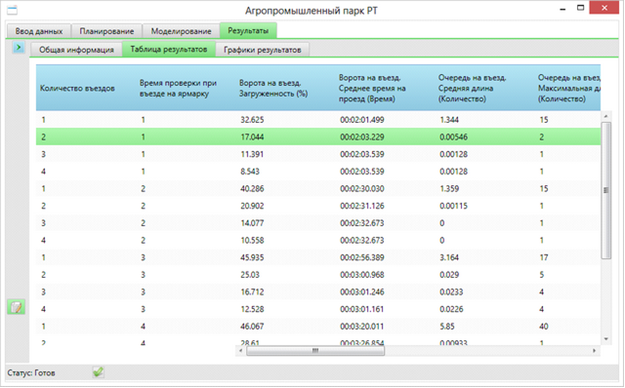
Рисунок 3.65. Вкладка «Таблица результатов» серии экспериментов
Планирование экспериментов
Имитация – это численный метод проведения экспериментов над математическими моделями сложных систем, подверженных случайным воздействиям
Любой численный метод имеет методическую ошибку. Цель планирования экспериментов - получение результатов с требуемой достоверностью при наименьших затратах. Планирование подразделяется на стратегическое и тактическое.
Стратегическое планирование
Для стратегического планирования используется концепция «черного ящика», суть которой - абстрагирование от физической сущности процессов, происходящих в моделируемой системе и выдаче заключений о ее функционировании только на основании входных и выходных переменных. Входные, независимые переменные называются факторами (x). Выходные – откликами (у), их величина зависит от значений факторов и параметров объекта исследования.
Структурная схема чёрного ящика представлена на рис.4.1.
| Имитационная модель |
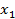
|
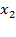
|
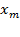
|
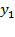
|
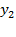
|
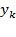
|
| Факторы |
| Отклики |
Рисунок 4.1. Структурная схема концепции черного ящика
При использовании концепции чёрного ящика должны выполняться следующие условия:
1. Рандомизация - случайность. Только при наличии случайности возможно корректное использование математического аппарата теории вероятностей и статистики.
2. Одновременное изменение всех факторов. Обеспечивает уменьшение стандартной ошибки при проведении экспериментов.
3. Последовательность планирования. Проведение экспериментов подразделяется на ряд последовательных этапов, и планирование каждого последующего этапа производится с учётом результатов, полученных на предыдущих этапах.
4. Кодирование. Не обязательно. Кодирование значительно упрощает расчёты и делает анализ результатов более наглядным, что весьма существенно при «ручной» обработке результатов. При применении ЭВМ кодирование также представляет некоторые преимущества в анализе результатов.
К факторам предъявляют следующие требования:
1. Легкая управляемость, что позволяет сравнительно несложно повторять проводимые эксперименты.
2. Факторы не должны являться функциями каких-то аргументов;
3. Факторы должны быть хотя бы линейно независимыми между собой, что позволяет упростить математическую модель, не вводя в неё произведения факторов между собой.
4. Любое сочетание факторов в стратегических планах не должно выводить объект из допустимого режима функционирования.
Планирование экспериментов зависит от вида математической зависимости, которую необходимо получить по результатам обработки. Если вид математической зависимости заранее не известен, то рекомендуется использовать степенные полиномы, позволяющие при увеличении степени полинома получать результаты с заданной достоверностью. Расчётная формула для вычисления коэффициентов полинома получается после преобразований:
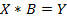
| (4.1) |
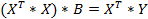
| |
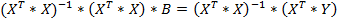
| |
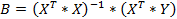
|
Рассмотрим пример представления математической зависимости результативного показателя эффективности от двух факторов, факторы в которой записаны в кодированном
виде:
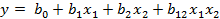
| (4.2) |
Пусть первый фактор представляет собой среднее время обслуживания, а второй фактор - среднее время между поступлением транзактов. В натурном виде они меняются в следующих диапазонах:
1. 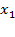 - меняется от 15 до 75 единиц времени.
- меняется от 15 до 75 единиц времени.
2. 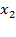 - от 100 до 300 единиц времени.
- от 100 до 300 единиц времени.
Рекомендуется кодированное представление факторов, которое определяет изменение любого фактора от -1 до +1, невзирая на то, в каких единицах он измеряется, в натурном виде и какие диапазоны изменения он занимает. Перевод факторов из натурного в кодированный вид поясняется в таблице 4.1.
Таблица 4.1. Перевод факторов из натурального в кодированный вид
| -1 | |||
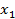
| |||
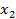
|
План полного факторного эксперимента.
В графическом виде план по проведению эксперимента представляет собой вершины квадрата, как это изображено на рис. 4.2.
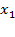
|
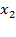
|
| 1,1 |
| 1,-1 |
| -1,1 |
| -1,-1 |
Рисунок 4.2. Графическое представление плана эксперимента
Вершины квадрата – план полного факторного эксперимента (ПФЭ). Обычно к этим точкам добавляется центральная точка, и пять проводимых экспериментов позволяют вычислить четыре коэффициента двухфакторной математической зависимости:
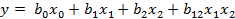
| 4.3 |
Этот же план можно представить в виде таблицы 4.2. Для обеспечения вычислений по одному и тому же алгоритму для всех коэффициентов к свободному члену полинома добавляется так называемый фиктивный фактор 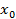 , который всегда равен единице.
, который всегда равен единице.
Таблица 4.2. План ПФЭ для двух факторов
| Факторы | 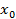
| 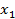
| 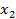
| 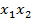
|
| ЦТ | ||||
| План ПФЭ | -1 | -1 | ||
| -1 | -1 | |||
| -1 | -1 | |||
План полного факторного эксперимента (ПФЭ) позволяет вычислить все коэффициенты степенного полинома, включая коэффициенты как при самих факторах, так и при всех сочетаниях факторов между собой в виде их произведений.
Достоинства плана ПФЭ.
1. Симметричность. Каждая точка плана имеет симметричные точки относительно осей координат. В математическом плане симметричность сводится к тому, что построчная сумма элементов всех столбцов плана, кроме левого, равна нулю.
2. Нормированность, которая в математическом плане сводится к тому, что построчная сумма квадратов элементов всех столбцов плана, кроме левого, равна 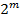 , где m – количество факторов.
, где m – количество факторов.
3. Ортогональность, которая заключается в независимости всех факторов друг от друга.
Кроме того, следует отметить сравнительную простоту составления плана ПФЭ, который представляет собой полный перебор совокупностей всех факторов по двум уровням. Таким образом, количество точек плана ПФЭ 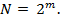 Отметим, что добавляемая к ним центральная точка не является точкой плана ПФЭ.
Отметим, что добавляемая к ним центральная точка не является точкой плана ПФЭ.
План ПФЭ имеет существенный недостаток, проявляющийся при сравнительно большом количестве факторов, так при m = 3, N = 8; при m = 7, N = 128, а при m = 10, N = 1024, что является неприемлемым.
План дробного факторного эксперимента
В некоторых случаях, если факторы независимы друг от друга, можно значительно уменьшить количество проводимых экспериментов, применяя план дробных факторных экспериментов (ДФЭ). В ДФЭ факторы разделяются на основные и дополнительные. Для основных факторов составляется план ПФЭ, а дополнительные меняются по законам изменения произведений основных факторов. Таким образом, если в эксперименте используется семь факторов, то по плану ПФЭ понадобилось бы провести 128 экспериментов. Если же они независимы друг от друга, то, выделив из них три основных фактора и составив для них план ПФЭ, можно ограничиться всего 9 экспериментами с учетом центральной точки. Планы ДФЭ сохраняют все названные достоинства планов ПФЭ.
Планы второго порядка
Если зависимость результативного показателя эффективности функционирования объекта исследования является нелинейной, для проведения экспериментов применяют планы второго порядка. На практике чаще всего для этого используют композиционные планы, в качестве ядра которых берутся рассмотренные ранее планы первого порядка ПФЭ и ДФЭ. Для получения требуемой нелинейной зависимости к планам первого порядка добавляются так называемые звездные точки по две на каждый фактор. Например, для двухфакторной зависимости добавляются четыре звездные точки. Составляется матрица планирования, а для вычисления всех коэффициентов по одному и тому же алгоритму к свободному члену b0 дописывается фиктивный фактор 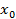 , который всегда равен 1.
, который всегда равен 1.
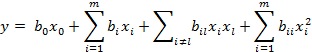
| (4.4) |
Для вычисления коэффициентов математической зависимости можно использовать ортогональный центральный композиционный план (ОЦКП) и ротатабельный центральный композиционный план (РЦКП). Планы второго порядка теряют названные ранее достоинства планов первого порядка ПФЭ и ДФЭ.
Композиционные планы ОЦКП и РЦКП имеют существенный недостаток, который начинает сказываться с увеличением количества факторов в проводимых экспериментах: чем больше факторов, тем больше расстояние звездных точек от центра осей координат, которое все больше и больше удаляется от заданных границ диапазонов изменения факторов, что является нежелательным.
Ортогональный центральный композиционный план
ОЦКП сохраняет свойство симметричности плана из-за того, что на каждый фактор вводят по две симметричные звездные точки.
Количество проводимых экспериментов:
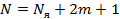 ,
,
где 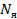 - число экспериментов в ядре плана,
- число экспериментов в ядре плана, 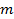 – число факторов.
– число факторов.
Ядром плана является ПФЭ или ДФЭ.
Если число факторов 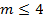 , то ядром плана является ПФЭ и число экспериментов в плане равно
, то ядром плана является ПФЭ и число экспериментов в плане равно 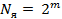 .
.
Если число факторов 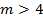 , то ядром плана является ДФЭ и число экспериментов в плане равно
, то ядром плана является ДФЭ и число экспериментов в плане равно 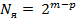 , где p – число взаимодействий, замененных факторами, учитываемыми в эксперименте.
, где p – число взаимодействий, замененных факторами, учитываемыми в эксперименте.
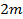 – это число экспериментов в «звездных точках», имеющих координаты:
– это число экспериментов в «звездных точках», имеющих координаты:

где 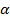 – величина «звездного плеча».
– величина «звездного плеча».
В центре плана – один эксперимент. Это точка факторного пространства с координатами 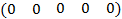 .
.
Для нахождения условий, обеспечивающих ортогональность, математическую зависимость 4.4 можно записать в виде:
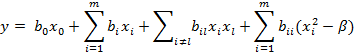
| 4.5 |
где 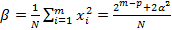 .
.
Величина 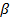 вводится для обеспечения ортогональности плана.
вводится для обеспечения ортогональности плана.
Матрицу планирования экспериментов для двух факторов можно представить в виде таблицы 4.3. В качестве ядра плана используется ПФЭ.
Число экспериментов равно
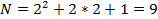
«Звездное плечо» 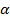 можно определить по формуле:
можно определить по формуле:
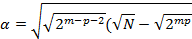
Значения 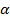 и
и 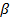 , обеспечивающие ортогональность плана при различных значениях
, обеспечивающие ортогональность плана при различных значениях 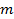 , приведены в таблице 4.4.
, приведены в таблице 4.4.
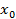 - фиктивный параметр, соответствующий коэффициенту
- фиктивный параметр, соответствующий коэффициенту 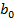 .
.
Таблица 4.3. План ОЦКП для двух факторов
| Факторы | № эксперимента | 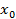
| 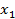
| 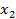
| 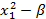
| 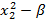
| 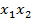
|
| Центральная точка | 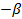
| 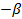
| |||||
| Ядро плана ПФЭ | 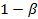
| 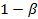
| |||||
| -1 | 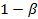
| 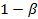
| -1 | ||||
| -1 | 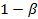
| 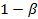
| -1 | ||||
| -1 | -1 | 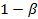
| 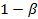
| ||||
| Эксперименты в звездных точках | 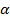
| 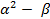
| 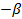
| ||||
- 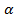
| 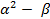
| 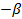
| |||||
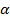
| 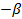
| 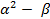
| |||||
- 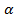
| 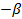
| 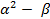
|
Таблица 4.4. Параметры ОЦКП
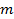
| Ядро плана | N | 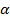
| 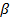
|
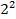
| 1,000 | 0,6667 | ||
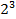
| 1,215 | 0,7300 | ||
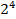
| 1,414 | 0,8000 | ||
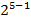
| 1,547 | 0,7700 | ||
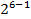
| 1,722 | 0,8430 | ||
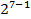
| 1,885 | 0,9000 | ||
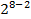
| 2,001 | 0,8889 |
В графическом виде план по проведению эксперимента представляет собой квадрат, как это изображено на рис.4.3.
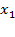
|
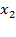
|
| 1,1 |
| 1,-1 |
| -1,1 |
| -1,-1 |
| -1,0 |
| 1,0 |
| 0,-1 |
| 0,1 |
Рисунок 4.3. Графическое представление плана эксперимента
Для 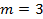 геометрической интерпретацией ПФЭ является куб, «звездные точки» ОЦКП лежат за пределами куба, т.к. они расположены на расстоянии большем, чем ±1 от центра плана, и лежат на поверхности сферы диаметром
геометрической интерпретацией ПФЭ является куб, «звездные точки» ОЦКП лежат за пределами куба, т.к. они расположены на расстоянии большем, чем ±1 от центра плана, и лежат на поверхности сферы диаметром 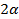 .
.
Ротатабельный центральный композиционный план
Метод РЦКП позволяет получить более точное математическое описание, что достигается благодаря увеличению числа опытов в центре плана и специальному выбору величины «звездного плеча».
Количество проводимых экспериментов:
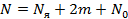 ,
,
где 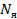 - число экспериментов в ядре плана,
- число экспериментов в ядре плана, 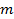 – число факторов.
– число факторов.
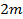 – это число экспериментов в «звездных точках», имеющих координаты:
– это число экспериментов в «звездных точках», имеющих координаты:

где 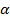 – величина «звездного плеча».
– величина «звездного плеча».
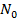 – число экспериментов в центре плана с координатами
– число экспериментов в центре плана с координатами 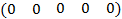 .
.
Ядром плана является ПФЭ и ДФЭ.
Характеристики РЦКП приведены в таблице 4.5.
Таблица 4.5. Параметры РЦКП
| Ядро плана | 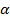
| 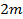
| 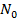
| 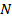
|
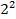
| 1,414 | ||||
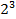
| 1,682 | ||||
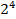
| 2,000 | ||||
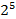
| 2,378 | ||||
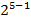
| 2,000 | ||||
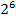
| 2,828 | ||||
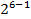
| 2,378 | ||||
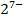
| 3,333 | ||||
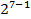
| 2,828 |
Чтобы композиционный план был рототабельным, величина «звездного плеча» 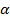 выбирается из условий:
выбирается из условий:
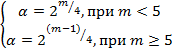
Матрица планирования строится так же, как и при ОЦКП. Отличие состоит только в том, что число экспериментов в центре плана выбирается из условия, что бы информация о значениях выходной переменной оставалась неизменной (или почти неизменной) для точек сферы единичного радиуса, т.е. что бы информационный профиль мало отличался внутри этой сферы. Планы, удовлетворяющие этому условию, называются рототабельными униформ-планами. Матрица РЦКП для двух факторов приведена в таблице 4.6.
Таблица 4.6. План РЦКП для двух факторов
| Факторы | № эксперимента | 
| 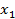
| 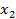
| 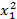
| 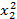
| 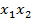
|
| Центральная точка | 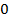
| ||||||
| Ядро плана ПФЭ | |||||||
| -1 | -1 | ||||||
| -1 | -1 | ||||||
| -1 | -1 | ||||||
| Эксперименты в звездных точках | 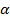
| 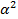
| 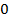
| ||||
- 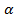
| 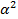
| 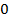
| |||||
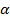
| 
| 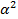
| |||||
- 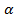
| 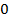
| 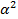
|
В графическом виде план по проведению эксперимента представляет собой квадрат, как это изображено на рис.4.4.
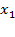
|
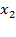
|
| 1,1 |
Рисунок 4.4. Графическое представление плана эксперимента
D - оптимальные планы
В D-оптимальных планах значения факторов не выходят за установленные границы диапазонов их изменения. Кроме того, они обладают еще одним существенным достоинством, обеспечивая минимальную ошибку во всем принятом диапазоне изменения факторов. На практике наиболее часто применяются планы Коно и планы Кифера.
Планы Коно
Для многофакторных экспериментов в геометрической интерпретации диапазон изменения факторов представляется многомерным кубом, который далее будем называть просто куб. Для двух факторов этот куб вырождается в квадрат. Эксперименты по плану Коно проводятся в вершинах куба, серединах ребер и центре куба. Характерной особенностью D-оптимальных планов является разница в количестве проводимых экспериментов для точек плана
различного вида. Приняты следующие удельные веса видов точек для двухфакторных экспериментов в планах Коно:
1. Вершины куба – 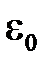 = 0,148.
= 0,148.
2. Середины ребер – 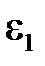 = 0,078.
= 0,078.
3. Центр куба – 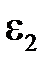 = 0,096.
= 0,096.
Расположение точек стратегического плана Коно на квадрате и кубе представлено на рис. 5.3.
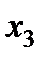
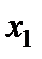
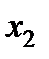
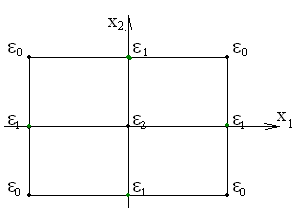
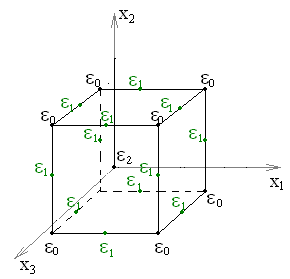
Рис. 5.3. Геометрическая интерпретация двухфакторного плана Коно
на квадрате и трехфакторного – на кубе
Количество точек для двухфакторного эксперимента (m = 2) и трехфакторного эксперимента (m = 3) приведено в табл. 5.4.
Таблица 5.4
| m = 2 | m = 3 |
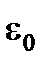 = 4 = 4
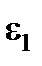 = 4 = 4
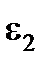 = 1 = 1
| 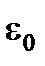 = 8 = 8
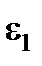 = 12 = 12
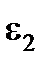 = 1 = 1
|
Планы Кифера
Эксперименты по плану Кифера проводятся в вершинах куба, серединах ребер и центрах граней. Для двухфакторных экспериментов по плану Кифера приняты следующие удельные веса.
1. Вершины куба – 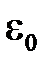 = 0,1458.
= 0,1458.
2. Середины ребер – 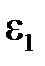 = 0,08015.
= 0,08015.
3. Центры граней – 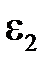 = 0,0962.
= 0,0962.
Расположение точек плана для двухфакторных и трехфакторных экспериментов представлено на рис. 5.4.
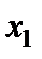
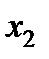
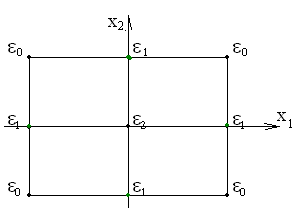
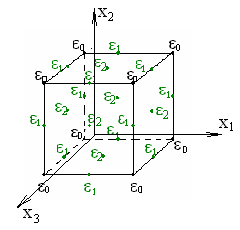
Рис. 5.4. Геометрическая интерпретация двухфакторного плана Кифера на квадрате и трехфакторного – на кубе
Количество точек в D-оптимальных планах Кифера приведено в табл. 5.5.
Таблица 5.5
| m = 2 | m = 3 |
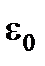 = 4 = 4
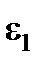 =4 =4
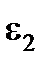 =1 =1
| 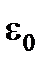 =8 =8
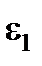 =12 =12
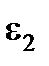 =6 =6
|
В табл. 5.6 приведем план Коно для двухфакторного экспериментав табл. 5.7 – план Кифера, которые позволяют построить математическую зависимость вида:
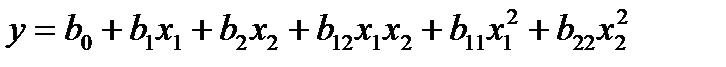
| (5.8) |
Таблица 5.6
| I | 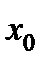
| 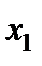
| 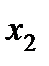
| 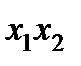
| 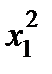
| 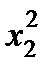
| 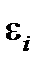
|
| –1 | –1 | 0,148 | |||||
| 0,078 | |||||||
| 0,148 | |||||||
| –1 | 0,078 | ||||||
| 0,096 | |||||||
| 0,078 | |||||||
| –1 | –1 | 0,148 | |||||
| –1 | –1 | 0,078 | |||||
| –1 | –1 | 0,148 |
Таблица 5.7
| I | 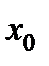
| 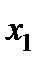
| 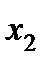
| 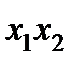
| 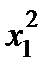
| 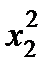
| 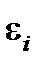
|
| –1 | –1 | 0,14580 | |||||
| 0,08015 | |||||||
| 0,14580 | |||||||
| –1 | 0,08015 | ||||||
| 0,09620 | |||||||
| 0,08015 | |||||||
| –1 | –1 | 0,14580 | |||||
| –1 | –1 | 0,08015 | |||||
| –1 | –1 | 0,14580 |
Отметим, что для того, чтобы не потерять корректность D-оптимальных планов и количество реализаций в каждом варианте было целым числом, общее количество проводимых экспериментов для планов Коно рекомендуется брать кратным 1000, а для планов Кифера – кратным 100000.
Дата добавления: 2015-01-13; просмотров: 3224;
