Вычисление основных статистических характеристик

Расчет описательных статистик производится при помощи модуля «Statistics/Basic Statistic/Tables». В этом модуле объединены наиболее часто использующиеся на начальном этапе обработки данных процедуры.

В панели модуля приводится перечень статистических процедур этого модуля:

1. Descriptive statistics - Описательные статистики.

2. Correlation matrices - Корреляционные матрицы.

3. t-test for independent groups - t-тест для независимых выборок.

4. t-test for dependent samples - t-тест для зависимых выборок.

5. Breakdown & one-wayANOVA - Классификация и однофакторный и дисперсионный анализ.

После выбора процедуры «Descriptive statistics» на экране появится одноименное диалоговое окно (рис.5.2).

Рисунок 5.2. Диалоговое окно «Descriptive statistics»

В этом окне при помощи кнопки «Variables» следует выбрать переменные для анализа (рис.5.3).

Рисунок 5.3. Окно выбора переменных

Чтобы выбрать статистики, подлежащие вычислению, необходимо перейти на вкладку «Advanced» (рис.5.4).

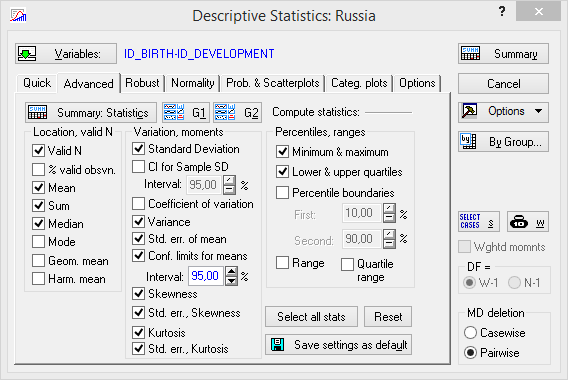
Рисунок 5.4. Диалоговое окно «Descriptive statistics\Advanced»

Список основных статистических характеристик:

1. Valid N - объем выборки.

2. Mean - среднее арифметическое. Среднее значение случайной величины представляет собой наиболее типичное, наиболее вероятное ее значение, своеобразный центр, вокруг которого разбросаны все значения признака.

3. Sum – сумма.

4. Median – медиана. Медианой является такое значение случайной величины, которое разделяет все случаи выборки на две равные по численности части.

5. Standard Deviation - стандартное отклонение. Стандартное отклонение (или среднее квадратическое отклонение) является мерой изменчивости (вариации) признака. Оно показывает на какую величину в среднем отклоняются случаи от среднего значения признака.

6. Variance – дисперсия. Дисперсия является мерой изменчивости, вариации признака и представляет собой средний квадрат отклонений случаев от среднего значения признака. В отличии от других показателей вариации дисперсия может быть разложена на составные части, что позволяет тем самым оценить влияние различных факторов на вариацию признака.

7. Standard error of mean - стандартная ошибка среднего. Стандартная ошибка среднего это величина, на которую отличается среднее значение выборки от среднего значения генеральной совокупности при условии, что распределение близко к нормальному. С вероятностью 0,68 можно утверждать, что среднее значение генеральной совокупности лежит в интервале + одной стандартной ошибки от среднего, с вероятностью 0,95 - в интервале + двух стандартных ошибок от среднего и с вероятностью 0,99 - среднее значение генеральной совокупности лежит в интервале + трех стандартных ошибок от среднего.

8. 95% confidence limits of mean - 95%-ый доверительный интервал для среднего. Интервал, в который с вероятностью 0,95 попадает среднее значение признака генеральной совокупности.

9. Minimum, maximum - минимальное и максимальное значения.

10. Lower, upper quartiles - нижний и верхний квартили. Верхний квартиль это такое значение случайной величины, больше которого по величине 25% случаев выборки. Верхний квартиль это такое значение случайной величины, меньше которого по величине 25% случаев выборки.

11. Range – размах. Расстояние между наибольшим (maximum) и наименьшим (minimum) значениями признака.

12. Quartile range - интерквартильная широта. Расстояние между нижним и верхним квартилями.

13. Skewness –асимметрия. Асимметрия характеризует степень смещения вариационного ряда относительно среднего значения по величине и направлению. В симметричной кривой коэффициент асимметрии равен нулю. Если правая ветвь кривой, начиная от вершины) больше левой (правосторонняя асимметрия), то коэффициент асимметрии больше нуля. Если левая ветвь кривой больше правой (левосторонняя асимметрия), то коэффициент асимметрии меньше нуля. Асимметрия менее 0,5 считается малой.

14. Standard error of Skewness -стандартная ошибка асимметрии.

15. Kurtosis – эксцесс. Эксцесс характеризует степень концентрации случаев вокруг среднего значения и является своеобразной мерой крутости кривой. В кривой нормального распределения эксцесс равен нулю. Если эксцесс больше нуля, то кривая распределения характеризуется островершинностью, т.е. является более крутой по сравнению с нормальной, а случаи более густо группируются вокруг среднего. При отрицательном эксцессе кривая является более плосковершинной, т.е. более пологой по сравнению с нормальным распределением. Отрицательным пределом величины эксцесса является число -2, положительного предела - нет.

16. Standard error of Kurtosis - стандартная ошибка эксцесса.

После нажатия на кнопку «Summary» окна «Descriptive statistics» на экране появится таблица с результатами расчетов описательных статистик (рис.5.5).

Рисунок 5.5. Окно с результатами расчета описательных статистик