Экономические индексы Ласпейреса, Пааше, Фишера. Индексы-дефляторы.

В рыночном хозяйстве особое место среди индексов качественных показателей отводится индексам цен. Основным назначением индекса цен является оценка динамики цен на товары производственного и непроизводственного потребления. Помимо этого индекс цен выполняет роль общего измерителя инфляции при макроэкономических исследованиях; используется при корректировке законодательно устанавливаемого размера оплаты труда, установлении ставок налогов.

Индексы цен нужны при разработке технико-экономических обоснований и проектов строительства новых предприятий. Без них нельзя обойтись при пересчете основных показателей системы национальных счетов (совокупного общественного продукта, национального дохода, капитальных вложений и т.д.) из фактически действующих цен в сопоставимые.

В конце 19 века были построены две формулы индекса цен, которые используются в качестве основных в статистике.

Это формула, предложенная немецким ученым Пааше в 1874 г. и в качестве веса индекса берется объем выпущенной продукции отчетного периода:

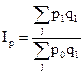
Немецкий ученый Э. Ласпейрес предложил определять индекс цен следующим образом в 1864 г., где в качестве веса берется объем выпущенной продукции базисного периода:

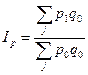
Индексируемой величиной обоих индексов является цены. Весами в же индексе цен Пааше выступает количество продукта текущего периода, а индексе цен Ласпейреса – количество продукции базисного периода. Значения этих индексов не совпадают и отличие объясняется тем, что индексы имеют различное экономическое содержание..

Индекс цен, исчисляемый по формуле Пааше, дает ответ на вопрос, насколько товары в текущем периоде стали дороже, чем в базисном. Индекс цен Ласпейреса показывает, во сколько бы раз товары базисного периода подорожали из-за изменения цен на них в отчетный период.

До начала 90-х годов отечественная статистика отдавала предпочтение индексу цен Пааше. Сложность его расчета заключается в том, что взвешивание по весам отчетного периода требует ежегодного (ежеквартального, ежемесячного) сбора и обработки значительных объемов информации для формирования системы весов. А это требует больших затрат трудовых и материальных ресурсов. Поэтому, начиная с 1991 г. отечественная статистика определяет индексы цен по формуле Ласпейреса, которой отдается предпочтение и в зарубежной статистике. При исчислении индекса цен по формуле Ласпейреса веса фиксируются на уровне базисного периода и остаются неизменными в течении некоторого промежутка времени, отсюда целью расчета индекса является измерение динамики стоимости базисного объема продукции.

Следует отметить, что индекс цен всегда имеет определенную степень условности. Это связано прежде всего с тем, что при его расчете учитываются изменение цен не по всей совокупности продукции, а по отдельным товарам, которые представляют так называемую товарную корзину. По мере отдаления от базисного года эта товарная корзина должна периодически пересматриваться. Только тогда она будет отражать реальную структуру объема производства. Особенно это важно в период резкого изменения экономических условий в народном хозяйстве.

Рассмотрим более подробно свойства индексов Ласпейреса и Пааше. Для удобства введем следующие обозначения:

I^П_р, I^П_q – индекс цен, физического объема продукции с текущими весами (индекс Пааше)

I^Л_р, I^Л_q – индекс цен, физического объема продукции с базисными весами (индекс Ласпейреса)

Свойство 1.

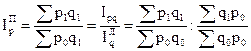
т.е. индекс цен в формуле Пааше равен отношению индекса стоимости продукции к индексу физического объема в формуле Ласпейреса.

Свойство 2.

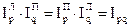
Свойство 3.

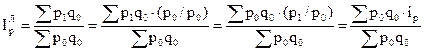
Если имеются индивидуальные индексы цен, то индекс цен по формуле Ласпейреса может быть исчислен как средняя арифметическая величина, где в качестве весов используется стоимость продукции базисного периода (р₀q₀). Именно этот способ определения цен наиболее часто используется на практике.

Индекс цен американского ученого И. Фишера представляет собой среднюю геометрическую из произведения двух агрегатных индексов цен Ласпейреса и Пааше.

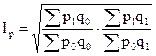
Эта формула имеет один недостаток: она лишена конкретного экономического содержания. Фишер назвал эту формулу идеальной формулой, идеальность которой заключается прежде всего в том, что индекс является обратимым во времени, т.е. при перестановке базисного и отчетного периодов полученный обратный индекс – это обратная величина первоначального индекса. Индекс Фишера в силу сложности расчета и трудности экономической интерпретации на практике используется довольно редко. Чаще всего он применяется при вычислении индексов цен за длительный период времени для сглаживания тенденций в структуре и составе объема продукции, в которых происходят значительные изменения.

Пересчет важнейших стоимостных показателей системы национальных счетов из фактических цен в сопоставимые осуществляется при помощи индекса-дефлятора. Дефлятор – это коэффициент, переводящий значение стоимостного показателя за отчетный период в стоимостные показатели базисного.

Индекс-дефлятор рассчитывается как отношение фактической стоимости продукции отчетного периода к стоимости объема продукции, структура которого аналогична структуре отчетного года, но определенного в ценах базисного года. В основе расчета индекса-дефлятора лежит формула Пааше – агрегатная формула индекса с текущими весами. Индекс-дефлятор для ВВП в 1992 г. определяется по формуле:

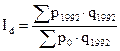
где I_d – индекс-дефлятор,

q₁₉₉₂ – объем продукции в 1992 г.,

p₀, p₁₉₉₂ – цены базисного периода и 1992 года соответственно

Реальный ВВП за 1992 год определяется по формуле:

R₁₉₉₂ = Q₁₉₉₂ ^.I_d

где Q₁₉₉₂ – номинальный ВВП

Важной особенностью индекса-дефлятора является то, что он не может быть использован для сравнительной оценки динамики цен за два периода. Индексы-дефляторы дают представление только об отношении стоимости продукции в текущем периоде к её стоимости в базисном периоде. При этом не учитывается отличие состава и структуры продукции в базисный период по сравнению с отчетным.

В статистической практике индексы-дефляторы определяются не только в целом по народному хозяйству, но и по отдельным регионам, различным товарным группам и т.д.