Границы и условия применения индексного метода
Индексный метод предполагает, что связь между признаками является жестко детерминированной, которая проявляется как в каждом отдельном случае (для отдельного товара, вида продукции, предприятия), так и в совокупности. Связь, изучаемая с помощью индексов, выражается в виде уравнения связи:
мультипликативного: 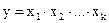
аддитивного: 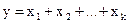
Вид функции, число переменных факторов (сомножителей или слагаемых) определяется логикой связи. многофакторная мультипликативная модель строится путем последовательного расчленения одного из факторов на составляющие.
Например, можно записать следующее уравнение связи:
|
|
|
= ..
Эту модель можно детализировать, тогда она будет включать не два, а 5 факторов.
|
|
|
|  |
= . . . .
Если мультипликативная модель имеет в качестве результативного первичный признак, то она называется полной. Примером такой модели является приведенный выше пример.
В корреляционном анализе, измеряя корреляцию между результатом и фактором, мы получаем полную меру корреляции независимо от того, как реализуется связь – непосредственно или опосредованно через влияние других неучтенных факторов. В индексном анализе мы измеряем только прямое влияние изменения фактора на изменение результата.
При построении уравнения связи иногда допускаются отступления от логики ради обеспечения увязки признаков, получения жестко детерминированной связи. Поэтому можно встретить уравнения связи, в которых не все составляющие элементы экономически обоснованы, нередки случаи появления среди факторов обратных величин. Это приводит к необоснованным выводам.
Применять только один индексный анализ недостаточно, т.к. уравнение связи как жестко детерминированная функция может быть построено только для некоторого числа факторов, которые непосредственно влияют на результат. Такие факторы могут оказаться недостаточными для объяснения его динамики. Для более полного описания связи между факторами необходимо использовать комплексный индексный и регрессионный анализ.
методика такого анализа такова. Определяется жестко детерминированное уравнение связи 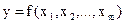 и строится уравнение регрессии для каждого компонента хj, на которые влияют свои факторы более низкого уровня.
и строится уравнение регрессии для каждого компонента хj, на которые влияют свои факторы более низкого уровня.
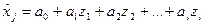
Оценив значимость каждого параметра отдельных регрессий, устанавливается круг причин каждого из хj, общий круг причин для пар факторов хi и хj ( 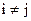 ). Используя полученное на основе регрессии значение
). Используя полученное на основе регрессии значение 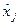 , мы получаем возможность измерить влияние каждого фактора на у. Далее вычисляются значения
, мы получаем возможность измерить влияние каждого фактора на у. Далее вычисляются значения 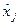 для базисного и отчетного периода и строится индекс следующим образом (при изучении влияния факторов х и w на у):
для базисного и отчетного периода и строится индекс следующим образом (при изучении влияния факторов х и w на у):
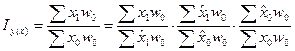
Если уравнение регрессии построено верно, то расхождения фактических и расчетных значений х для базисного и отчетного периодов будут незначительны и первый и последний индексы будут близки к единице.
Центральное место принадлежит второму индексу системы – он измеряет влияние на у изменений в расчетных значениях 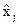 . Он описывает влияние на у факторов второго уровня (не жестко детерминированных) и силы их воздействия (коэффициенты аi из уравнений регрессии).
. Он описывает влияние на у факторов второго уровня (не жестко детерминированных) и силы их воздействия (коэффициенты аi из уравнений регрессии).
Содержание
| Введение ….………………………………………………………………………….. | |
| Раздел I. Описательная статистика ………………………………………………… | |
| Тема 1. Статистика как наука. Методы статистики ………………………………. | |
| Тема 2. Статистические показатели. Представление статистических данных …………...……………………… | |
| Тема 3. Статистическая группировка ……………………………………………… | |
| Тема 4. Средние величины …………………………………………………………. | |
| Раздел II. Аналитическая статистика ……………………………………………… | |
| Тема 5. Вариация массовых явлений. Показатели вариации ……………………. | |
| Тема 6. Выборочное наблюдение ………………………………………………….. | |
| Тема 7. Статистическое изучение взаимосвязи социально-экономических явлений ………………………………………. | |
| Тема 8. Статистическое изучение динамики социально-экономических явлений ………………………………………. | |
| Тема 9. Экономические индексы …………………………………………………... |
.
Дата добавления: 2015-03-03; просмотров: 1580;
