Основные модели экономического роста.

Нейтрализация отрицательных проявлений и развитие положительных тенденций экономического роста возлагается на государственное регулирование экономики. На вооружении государственного регулирования экономического роста имеются различные экономические модели.

Все предлагаемые модели представляются вполне рациональными. Они не исключают, а дополняют друг друга.

Модели представляют собой математические уравнения, которые выражают реальные экономические процессы в абстрактном и упрощенном виде. Те величины, которые находятся вне модели, принято называть экзогенными, а те, которые определяются с помощью модели - эндогенными. Любая модель увязывает те или иные экзогенные и эндогенные параметры. Создать модель означает не что иное, как найти функцию (оператор), связывающую названные параметры.

Современные теории экономического роста, которые нашли свое отражение в экономико-математических моделях, сформировались на основе двух источников: неоклассической теории уходящей своими корнями к теоретическим взглядам Ж.-Б.Сэя и получившей законченное выражение в работах Дж. Б. Кларка (СЩА), и кейнсианской теории макроэкономического равновесия.

Основным регулирующим фактором экономического роста являются инвестиции. В момент осуществления они повышают совокупный спрос, а в последующем, увеличивают совокупное предложение. Именно колебания инвестиций в соответствии с кейнсианской теорией, вызывают колебания в производстве национального дохода, порождают цикличность развития рыночной экономики.

Кейнсианская модель. Это простейшие модели, используемые в качестве математического инструментария для изучения экономической динамики и факторов, ее определяющих, а также для построения прикладных макроэкономических моделей и описания связи глобальных экономических показателей. Они, как и учение в целом, основаны на главенствующей роли спроса в обеспечении макроэкономического равновесия. Решающий элемент
спроса — инвестиции, которые посредством мультипликатора увеличивают прибыль. Одновременно они сами вызваны к жизни ростом прибыли, так как капитальные вложения представляют собой функцию увеличения прибыли. Отметим, что кейнсианцы не разделяют неоклассическую позицию эффективности производственных факторов и их взаимозаменяемости.

Американские экономисты Р. Харрод и Е. Домар еще в
50-е гг. отметили некоторые отличительные черты кейнсианского подхода к анализу проблем экономического роста: спрос не равен автоматически предложению, сбережения - инвестициям; важнейшую роль в экономическом росте играет формирование спроса и, прежде всего, спроса на инвестиции; основные технологические коэффициенты и пропорции не меняются вследствие негибкости цен и определяются техническим прогрессом.

В соответствии с кейнсианскими моделями норма накопления (сбережения) - главный стратегический фактор и основной параметр регулирования долговременного роста экономики. Этот рост устойчив, если устойчивы доля сбережений в доходе и отношение «капитал/продукт» (это гарантированный темп роста). Однако такая устойчивость не достигается автоматически. Отклонения фактического темпа роста от гарантированного порождают цикли­ческие колебания. Отклонения гарантированного от естественного темпа роста, т. е. темпа, соответствующего темпу роста населения, вызывают длительные отрицательные тенденции в форме экономической стагнации или инфляции. Поддержание устойчивого роста экономики требует государственного вмешательства, а именно - регулирования накопления и потребления с помощью мер фискальной и кредитно-денежной (монетарной) политики.

Модель Е. Домара. Это простейшая посткейнсианская модель. В ней в явном виде присутствует только рынок благ. Фактором увеличения совокупного спроса и, соответственно, совокупного предложения выступает прирост инвестиций. Рассматривая модель Домара, отметим, что в ней, в отличие от первоначальных кейнсианских моделей,
инвестиции — фактор создания не только дохода, но и новых мощностей. Динамическая сбалансированность спроса и предложения, по Домару, определяется динамикой капитальных вложений, которые образуют новые мощности и новые доходы. Следовательно, задача сводится к определению объема и динамики инвестиций. Е. Домар предложил для решения систему из трех уравнений: уравнение предложения, уравнение спроса, уравнение спроса и предложения совместно.

1. Уравнение предложения:

Δ Х = i σ

где: X - прирост производства, i - объем капитальных вложений, σ - средняя производительность капитальных вложений. 1: X - составляет прирост продукции за счет единицы капитальных вложений. В этом уравнении учитываются НТП, занятость, природные ресурсы.

2. Уравнение спроса:

М = Δ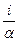

где α — средняя склонность к сбережениям, обратная величина которой определяет величину мультипликатора. В данном уравнении учитывается лишь прирост инвестиций. Основное уравнение (макроэкономического равновесия — равенство между приростом доходов и приростом производства:

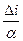= i σ

Исходя из него, получаем норму роста капитальных вложений. Модель Домара однофакторная и однопродуктовая, в ней учтены лишь инвестиции и один продукт.

Модель Р.Харрода К аналогичным выводам на несколько лет раньше пришел Р.Харрод. Как и в предыдущей модели, норма уравновешенного роста является функцией соотношения роста доходов и капитальных вложений, что дает повод называть эти модели моделями Харрода-Домара. Однако если модель Домара базируется на использовании мультипликатора, то в основе модели Харрода лежит теория акселератора, и, следовательно, она определяет норму сбалансированного роста доходов, с которой связаны капитальные вложения. Харрод особое внимание уделяет занятости рабочей силы при экономическом росте.

Модель Харрода позволяет на базе теории акселератора исследовать инвестиционные решения предпринимателей, где — ускорение.

Напомним, что принцип акселератора отражает и реальные связи между производством товаров для населения и производством капитальных товаров. Если спрос и доходы стабильны, то инвестиции необходимы лишь для обновления капитала. При росте потребительского спроса для расширения производства необходимы так называемые чистые капитальные вложения. Последние должны расти быстрее спроса, так как они долгосрочные. Формула акселератора:

Харрод исходит из двух посылок. Во-первых, накопление представляет постоянную долю национального дохода, оно растет темпами, равными темпам роста доходов, предельная и средняя склонность к накоплению равны между собой. Во-вторых, объем осуществляемых капиталовложений есть функция прироста дохода или спроса между Двумя периодами. Согласно основному уравнению Кейнса для равновесия сумма сбережений должна быть равна сумме инвестиций. Отсюда следует, что норма роста, умноженная на капитальный коэффициент, равна удельному весу накоплений в национальном доходе.

Для различных норм роста Харрод выдвигает следующее положение:система свободного предпринимательства (к которой идет наша страна) будет эффективно функционировать, если доходы будут расти ускоренными темпами. Инвестиции должны предвосхищать динамику потребительского спроса. Равновесие по этой модели весьма неустойчиво. Отсюда следует, что необхо­димо вмешательство государства через финансовую политику. Модель Харрода послужила толчком для разработки моделей Д.Хикса, Р.Гудвина и др.

Р. Харродом и Е. Домаром были созданы и проанализированы и другие ва­рианты модели. Особый интерес для российской экономики представляет вари­ант, основанный на различном подходе к инвестициям: с одной стороны, уве­личение выпуска продукции достигается при неизменной эффективности ин­вестиций (т. е. без учета влияния технического прогресса и роста производи­тельности труда и капиталоотдачи), с другой — при изменении их эффективно­сти (с учетом этих факторов).

Для случая, когда увеличиваются размеры капитала, потребляемого на про­изводство единицы продукции, либо возрастает объем капитала, приходящегося на данную массу рабочей силы, в модель вводится коэффициент потребности в капитале ( он обусловлен приростом капиталоемкости продукции — приростом капитала на единицу выпускаемой продукции).

Темп роста продукции в данном варианте модели Р. Харрода и Е. Домара ставится в зависимость от трех факторов: нормы сбережения, коэффициента потребности в капитале и изменения эффективности инвестиций.

Неоклассические модели. В центре неоклассического направления стоит идея оптимальности рыночной системы, рассматриваемой как совершенный саморегулирующийся механизм, позволяющий наилучшим образом всех производственные факторы не только отдельному экономическому субъекту, но и экономике в целом.

В реальной экономической жизни общества это равновесие нарушается. Однако моделирование равновесия позволяет найти отклонение реальных процессов от идеала. Наиболее разработанными и применяемыми стали: факторная модель Кобба-Дугласа, простая односекторная модель экономической динамики Р.Солоу, модель краткосрочного экономического равновесия Дж.Кейнса и модель динамического равновесия Харрода-Домара.

Важнейшей предпосылкой неоклассической теории являлась идея о нали­чии свободной конкуренции и установлении доли производственных факторов на уровне их предельных продуктов, что обеспечивало устойчивость экономического равновесия. На базе этих предпосылок экономисты неоклассического направления предложили свой вариант модели экономического роста. Это -производственная функция Кобба-Дугласа. Была выведена система показателей, характеризующих зависимости между затратами и выпуском продукции (коэффициенты эластичности выпуска по ресурсам), между самими затратами (предельная норма замещения и эластичность замещения ресурсов); была дана система количественных характеристик для экономического обоснования тех­нического прогресса: нейтрального и влияющего на соотношение эффективно­сти производственных факторов, материализованного, т. е. воплощенного в средствах производства, и нематериализованного, не воплощенного в средствах производства.

Эмпирическая оценка параметров производственных функции - важный аппарат анализа количественных взаимосвязей, определяющих потенциально возможный выпуск продукции. На основе этих оценок был сделан, в частности вывод, что главными стратегическими факторами долговременного экономического роста стал технический прогресс и определяющие его предпосылки: повышение качества оборудования, рост квалификации рабочей силы и уровня организации производства.

Экономисты неоклассического направления использовали производственную функцию не только для получения эмпирических оценок, но и как подходящую математическую форму для трактовки проблем динамического равновесия экономики. Они пытались доказать, что экономика внутренне устойчива и обладает необходимыми механизмами для автоматического восстановления нарушенного равновесия. Государственное вмешательство в экономику, по их мнению, должно быть сведено к минимуму и ограничиваться преимущественно сферой кредитно-денежной политики. Что касается механизма распределения национального дохода, то, согласно этой теории, каждый производственный фактор (труд и капитал) получает долю продукции в соответствии со своим объемом и предельной производительностью. Изменение этих долей происходит только под влиянием не нейтрального технического прогресса.

Факторная модель экономического роста. Производственная функция союз экономистов с математиками. Среди существующих в теории и применяемых на практике моделей экономического роста наиболее функциональными являются неоклассические факторные модели экономического роста, основой которых служит аппарат так называемых производственных функций. Среди аналитических инструментов неоклассических моделей главное место принадлежит производственной функции.

Производственная макроэкономическая функция - это соотношение между объемом выпуска и определяющими его динамику взаимосвязанными факторами производства. Если предположить, что развитие техники и технологии производства приводит к одинаковому увеличению предельного про­дукта капитала и труда, а также абстрагироваться от такого экономического ресурса, как земля, то обычная неоклассическая производственная функция будет иметь следующий вид

Y = f (K,N),

где К - капитал, N - труд.

С помощью данной двухфакторной модели производственной функции можно кратко проанализировать ее возможности.

Во-первых, данная модель позволяет проиллюстрировать роль и вознаграждение каждого фактора производства в создании единицы общественного продукта. Для этого необходимо все показатели производственной функции выразить в расчете на душу населения. Разделив обе части управления на N, получим функцию производительности труда от капиталовооруженности :

Y =f (k), где

у = 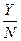- производительность общественного труда; k = -обьем общественного капитала, приходящегося на одного работника.

В конце 20-х гг. экономист П.Дуглас и математик Х.Кобб (оба — США) обработали три временных ряда характеристик американской обрабатывающей промышленности за 1899-1922 гг., рассмотрев рост основного капитала, количество отработанных часов и объем производства. Исследование показало, что за выделенный период основной капитал вырос в 4 раза, капиталовооруженность — в 2,7, число отработанных часов — в 1,61, а физический объем производства — в 2,4 раза. Исходя из того, что производст­венная функция должна быть линейной и гомогенной, они предложили следующую эмпирическую формулу:

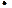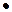y = 1,01 L K ,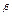

где у — объем производства; L — затраты труда, К - затраты капитала, «α» и «β» — степенные коэффициенты. Дальнейшие расчеты дали значения: α = 3/4, β = 1/4. Примерно такие же значения приводятся в учебнике «Экономикс» П. Самуэльсона и В. Нордхауса. Расчеты по обрабатывающей промышленности СССР за 1961-1970 гг. (а это сравнительно благоприятный период ее роста) дали следующие значения: α = 0,72 » β = 0,28. Степенные показатели означают, насколько увеличится объем производства, если соответствующий производственный фактор увеличится на 1%.

Важнейшие черты функции Кобба-Дугласа при интерпретации ее в неклас­сическом духе можно сформулировать следующим образом:

- предполагается постоянство прибыли и удельных расходов, отсутствие накопления, сумма эластичности производства (труд и капитал) равна единице. Степень взаимозаменяемости факторов колеблется от 0 до 1 и обычно менее единицы. Пределы взаимозаменяемости ставит данный уровень технического развития;

- теоретически возможна безграничная замена труда капиталом;

- функция не учитывает изменения качества производственных факторов, т. е. технический прогресс элиминирован. Отсюда можно сделать вывод, что функция приемлема лишь для экстенсивного экономического роста.

Функция Кобба-Дугласа представляет собой частный случай производственной функции. Начало разработки неоклассических моделей экономического роста относится к середине XX столетия. Первым исследователем здесь стал Р. Солоу. Затем последовали модели, в которых стал учитываться технический прогресс.

Неоклассические модели в условиях уравновешенного спроса внесли изменчивость капитального коэффициента. Соотношение «капитал \ производство» становится гибким вследствие того, что неоклассические модели учитывают не один, а два производственных фактора, и предполагают их взаимозаменяемость. Кроме технической взаимозаменяемости факторов производства необходима предпосылка неоклассической концепции о господстве совершенной конкуренции на рынке факторов производства. Отсюда происходит и название этих моделей.

Модель Р.Солоу представлена системой следующих уравнений:

1. y = f(K,N),

2. у = C + S,

3. S = S 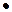y, где s-const,

4. S = K+μ 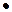K', где 0 < μ < 1, μ - const,

5. N = g 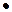N', g - const,

где у — общий выпуск продукции (он же — полный доход);

К - объем основного капитала;

N - численность занятых в производстве работников;

S - объем валового накопления (фонд накопления),

С - фонд потребления;

s - норма накопления,

g - коэффициент прироста рабочей силы,

K' - чистый прирост капитала,

N' - прирост рабочей силы

При этом:

- капиталовооруженность труда составит k = K/N;

- доля фонда потребления в общем выпуске продукции - (1 - S ),

- фонд потребления Z = ( 1 - S ) 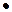у.

Фонд потребления экзогенно задается его долей в общем выпуске продукции. Из соотношений модели можно получить зависимость фонда потребления от уровня производительности, представить этот уровень как функцию от капиталовооруженности труда, а также определить размер инвестиций, необхо­димых для капиталовооруженности на неизменном уровне.

Р. Солоу в своей модели использует производственную функцию Кобба-Дугласа, в которой труд и капитал хорошо взаимозаменяют друг друга и сумма эластичности выпуска продукции по факторам производства равна единице (постоянная отдача от масштаба). Отсюда по Р.Солоу производственная функция принимает вид: у = f ( К, N ) .

В модели отсутствует функция совокупного спроса и предполагается, что спрос изменяется в таком же размере как и предложение.

Таким образом, в модели Р.Солоу средняя производительность труда есть функция его капиталовооруженности В модели Р. Солоу выпускается только один продукт, на производство которого затрачиваются капитал и труд. В отличие от модели Р. Харрода и Е. Домара фактором роста продукции в модели Р. Солоу выступает численность занятых в производстве работников. Рост численности занятых предполагается экзогенно заданным для любого момента времени, что предопределяет темп роста продукции и капитала при постоянных ценах. Рост ВНП становится возможным за счет различных комбинаций производственных факторов.

Механизм функционирования модели выглядит следующим образом. В каждый данный момент времени заданы численность занятых и объем капитала. Как только фактическая отдача этих факторов обеспечит полную занятость, для нахождения объема выпуска можно использовать производственную функцию:

y = f (K, N).

После этого склонность к сбережению покажет, какой объем выпуска будет использован на сбережения и инвестирован. Тем самым определяется чистое накопление капитала в текущем периоде. Прибавление этой величины к прежнему объему капитала даст его общий объем, доступный для использования в следующем периоде, и весь процесс расчетов можно производить снова.

Естественно, что неоклассические модели эффективны при совершенной конкуренции, хотя они в то же время рассматривают отклонения от нее.

Подробнее об этом см.: Гальперин В.М., Гребенников П.И., Ленусский А.И., Таразевич Л. С. Макроэкономика: Учебник. СПб.: Изд-во СПбГУЭФ, 1997, гл.13.