Рівняння електричних коливань
Розглянемо коло, до якого входить джерело струму з електрорушійною силою ε (в загальному випадку - змінною), індуктивність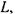 
ємність С та активний опір R, що з'єднані послідовно (мал. 2.25). Запишемо вираз, який пов'язує спад напруги на опорі 
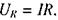напругу на конденсаторі 
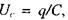напругу на індуктивності 
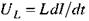та е.р.с. джерела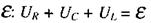 
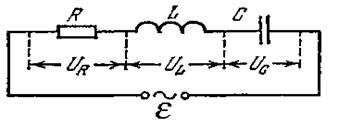
Мал. 2.25.
Оскільки за означенням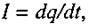 
після диференціювання за часом, одержимо диференційне рівняння електричних коливань:
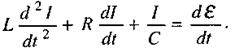(2.66)
Це рівняння виражає залежність сили струму від часу і є лінійним неоднорідним диференційним рівнянням другого порядку з постійними коефіцієнтами. Аналогічне рівняння можна отримати і для інших електричних величин (наприклад, заряду на конденсаторі q).
Вільні гармонічні коливання. Якщо джерело має постійну в часі ЕРС, тобто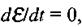 
то рівняння (2.66) стає однорідним. За аналогією з механічними коливаннями це є рівняння згасаючих коливань
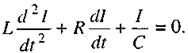(2.67)
За відсутності опору 
рівняння (2.67) перетворюється в рівняння вільних гармонічних коливань
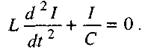
Розділивши ліву частину цього рівняння на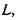 
матимемо:
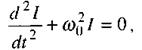(2.68)
де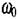 
- власна частота вільних електричних коливань
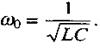(2.69)
Рівняння (2.68) має своїм розв'язком гармонічну функцію
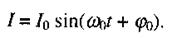(2.70)
Вираз, котрий стоїть під знаком синуса (або косинуса), називають фазою коливань 
У даному випадку 
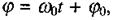де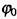 
- початкова фаза. Мінімальний проміжок часу, через який фаза повторює своє значення, називається періодом коливань. Період власних коливань
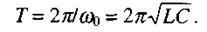(2.71)
Ця формула носить назву формули Томсона. Із зменшенням індуктивності котушки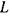 
та ємності конденсатора С зменшується період коливань, а значить зростає їхня частота.
Дата добавления: 2015-03-03; просмотров: 1135;