Хвильове рівняння. Поздовжні і поперечні хвилі
Припустимо, що хвильовий процес розповсюджується у додатному напрямку осі 0Х, а джерело коливань знаходиться в площині, перпендикулярній до напрямку розповсюдження, і коливається за законом 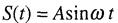 (мал. 1.29).
(мал. 1.29).
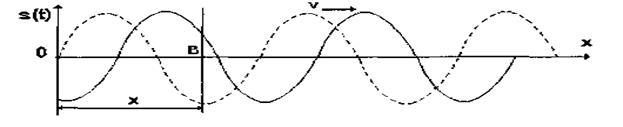
Мал. 1.29. Хвильовий процес.
Нехай 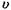 - швидкість розповсюдження хвильового процесу у середовищі. Через проміжок часу
- швидкість розповсюдження хвильового процесу у середовищі. Через проміжок часу 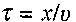 хвильовий процес досягне точки В, яка знаходиться на відстані х від джерела коливань, і викличе коливання цієї точки через час
хвильовий процес досягне точки В, яка знаходиться на відстані х від джерела коливань, і викличе коливання цієї точки через час 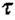 за законом:
за законом:
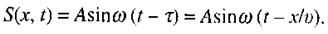 (1.57)
(1.57)
Рівняння (1.57) - це рівняння плоскої хвилі. Величину 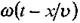 називають фазою хвилі. Геометричне місце точок, які коливаються в однаковій фазі, утворює хвильову або фазову поверхню. Поверхня, до якої дійшла хвиля у деякий момент часу, називається фронтом хвилі. У даному випадку фронт хвилі являє собою площину
називають фазою хвилі. Геометричне місце точок, які коливаються в однаковій фазі, утворює хвильову або фазову поверхню. Поверхня, до якої дійшла хвиля у деякий момент часу, називається фронтом хвилі. У даному випадку фронт хвилі являє собою площину 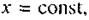 тому хвиля зветься плоскою. Форма хвильової поверхні визначається конфігурацією джерела коливань і властивостями середовища. В ізотропному середовищі від точкового джерела розповсюджується сферична хвиля, в якої хвильова поверхня є сфера.
тому хвиля зветься плоскою. Форма хвильової поверхні визначається конфігурацією джерела коливань і властивостями середовища. В ізотропному середовищі від точкового джерела розповсюджується сферична хвиля, в якої хвильова поверхня є сфера.
Під швидкістю розповсюдження хвилі розуміють швидкість розповсюдження фіксованої фази коливання. Дійсно, якщо 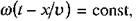 то після диференціювання цієї рівності отримаємо:
то після диференціювання цієї рівності отримаємо:
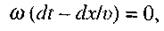
звідки 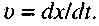
Як відомо, довжина хвилі 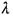 дорівнює відстані, яку проходить хвиля за час, що дорівнює періоду коливань:
дорівнює відстані, яку проходить хвиля за час, що дорівнює періоду коливань:
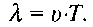
Враховуючи зв'язок між 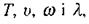 рівняння (1.57) можна
рівняння (1.57) можна
подати у вигляді:
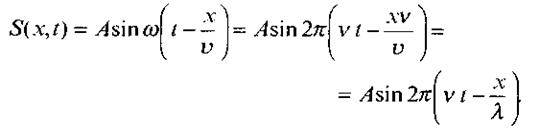
З рівняння плоскої хвилі випливає, що зміщення 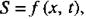 тобто хвиля має подвійну періодичність (як у просторі, так і у часі). Рівняння (1.57) є розв'язком диференційного рівняння другого порядку у частинних похідних:
тобто хвиля має подвійну періодичність (як у просторі, так і у часі). Рівняння (1.57) є розв'язком диференційного рівняння другого порядку у частинних похідних:
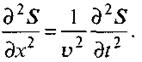 (1.58)
(1.58)
Рівняння ( .58) являє собою одновимірне хвильове рівняння плоскої хвилі. Якщо яка-небудь фізична величина описується таким хвильовим рівнянням, то це означає, що вона розповсюджується в просторі у вигляді плоскої хвилі зі швидкістю 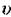 .
.
Дата добавления: 2015-03-03; просмотров: 2281;
