Напряженностьи потенциал — характеристики электрического поля

Силовой характеристикой электрического поля является напряженность, равная отношению силы, действующей в данной точке поля на точечный заряд, к этому заряду

Напряженность — вектор, направление которого совпадает с направлением силы, действующей в данной точке поля на положительный точечный заряд.

Напряженность электрического поля в произвольных точках аналитически задается следующими тремя уравнениями:

где Е_x, Е_y и Е_z — проекции вектора напряженности на соответствующие координатные оси, введенные для описания поля. Электрическое поле графически удобно представлять силовыми линиями, касательные к которым совпадают с направлением вектора напряженности в соответствующих точках поля.

Обычно эти линии проводят с такой густотой, чтобы число линий, проходящих сквозь единичную площадку, перпендикулярную им, было пропорционально значению напряженности электрического поля в месте расположения площадки.

Представим себе, что заряд q перемещается в электрическом поле дотраектории (рис. 12.1). Силы поля при этом совершают работу, которую можно выразить через напряженность [см. (12.1)]:

где dl — элементарное перемещение; Е_l— проекция вектора Е на направление dl. Покажем, что работа сил электростатического поля (электрического поля неподвижных зарядов) не зависит от траектории, по которой перемещается заряд в этом поле. Поля, обладающие таким свойством, называют потенциальными. Пусть заряд q переместился по замкнутой траектории 1-а-2-б-1 (рис. 12.1). Так как поле электростатическое, то положение зарядов, создающих поле, при этом не изменилось, и потенциальная энергия, зависящая от их взаимного положения, осталась прежней. Поэтому работа сил электростатического поля по перемещению заряда по замкнутой траектории равнанулю:

Так как силы, действующие на заряд q, определяются его положением в поле, то ражения для работ сил поля при перемещении заряда по одной и той же траектории в противоположных направлениях отличаются только знаком:

Подстановка этого выражения в(12.4) дает

Равенство (12.5) означает, что работа сил электростатического поля не зависит от траектории заряда, а зависит от величины заряда, положения начальной и конечной точек траектории и от напряженности поля.

На основании этого свойства вводят понятие разности потенциалов Δφ, которая для электростатического поля равна напряжению U.

Разностью потенциалов между точками поля называют отношение работы, совершаемой силами поля при перемещении точечного положительного заряда из одной точки поля в другую, к этому заряду:

где φ₁ и ф₂ — потенциалы в точках 1 и 2 электрического поля, U₁₂ — напряжение между этими точками. Разность потенциалов между двумя точками зависит от положения выбранных точек и от напряженности электрического поля, как следует из (12.6).

Наряду с разностью потенциалов в качестве характеристики электрического поля используют понятие потенциала. Однако для данной точки поля оно имеет однозначный смысл только в том случае, если задан потенциал какой-либо произвольной точки поля. На практике принято считать, что потенциал проводников, соединенных с землей, или потенциал шасси, на котором смонтировано радиоустройство (и в том и в другом случаях говорят о заземлении), равны нулю. В теоретических задачах обычно считают равным нулю потенциал бесконечно удаленных точек.

Вычислим потенциал поля точечного заряда,расположенного в однородном изотропном диэлектрике с диэлектрической проницаемостью ε (рис. 12.2). Пусть точки 1 и 2 находятся на одной силовой линии на расстояниях соответственно r₁ и r₂ от источника поля — заряда Q. Проинтегрируем выражение (12.6) по отрезку 1—2, учитывая, что в соответствии с законом Кулона (для точечного заряда)

где ε₀ ~ 8,85 • 10 ^-¹² Ф/м — электрическая постоянная.

Предположим, что потенциал в бесконечно удаленной точке равную нулю: φ₂ → 0 при r₂ →∞. Тогда из (12.7) получаем

или в более общем виде

Могли быть и другие предположения относительно значения потенциала в бесконечно удаленной точке, однако сделанное выше допущение привело к наиболее простому выражению (12.8), по которому обычно и вычисляют потенциал поля точечного заряда.

Потенциалы электрического поля в различных точках наглядно можно представить в виде поверхностей одинакового потенциала (эквипотенциальных поверхностей). Обычно проводят эквипотенциальные поверхности, отличающиеся от соседних на одно и то же значение потенциала. На рис. 12.3 изображены эквипотенциальные поверхности (штриховые линии) и силовые линии (сплошные) поля двух разноименных одинаковых точечных зарядов.

Аналитически зависимость электрического потенциала от координат в разных точках поля задается некоторой функцией координат

которая в частных случаях может иметь, например, вид (12.8). Так как напряженность электрического поля определяется через силу, а потенциал — через работу сил поля, то эти характеристики связаны между собой аналогично силе и работе. Интегральная зависимость напряженности поля и потенциала дается формулой (12.6) или выражением

Здесь с учетом знака «—» изменены пределы интегрирования: верхнему пределу интеграла соответствует в левой части уменьшаемое φ₂, нижнему — вычитаемое φ₁.

Получим дифференциальную связь между Е и φ. Предположим, что точки 2 и 1 расположены сколь угодно близко, тогда из (12.10)получим

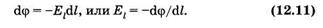
Производная от потенциала по направлению dφ/dl характеризует отношение приращения потенциала dφ к соответствующему расстоянию dl в некотором направлении l; E_l — проекция вектора Е на это направление.

Смысл формулы (12.11) виден из рис. 12.4. В точке 0 проведен вектор Е, который спроецирован на направления l_1, l₂ и 1₃. Эти проекции по модулю равны производным от потенциала по соответствующим направлениям: |dφ/dl₁|, |dφ/dl₂|, |dφ/dl₃|. Наибольшее изменение потенциала, приходящееся на единицу длины, происходит вдоль прямой, совпадающей с Е; знак «минус» в (12.Назначает, что потенциал быстрее всего убывает в направлении Е и быстрее всего возрастает в направлении - Е. Можно сказать, что вектор Е равен взятому с обратным знаком градиенту потенциала:

В направлении, перпендикулярном силовой линии, имеем

Из этого следует, что силовые линии и эквипотенциальные поверхности взаимно перпендикулярны.Если поле однородно, например поле плоского конденсатора, то из формулы (12.6) находим, что для двух точек, расположенных на одной силовой линии на расстоянии l,

Учитывая (12.11)и (12.9),можно записать проекции вектора напряженности электрического поля по трем координатным осям:

Тогда напряженность определяют по формуле

Если поле создано точечными зарядами, то напряженность в некоторой точке можно вычислить как векторную сумму напряженностей полей, создаваемых в этой точке каждым зарядом отдельно (принцип суперпозиции):

а электрический потенциал в этой точке — как алгебраическую сумму потенциалов от каждого заряда, предполагая, что потенциал бесконечно удаленных точек равен нулю:

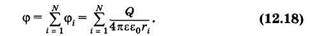
Существующие электроизмерительные приборы рассчитаны на измерение разности потенциалов, а не напряженности. Ее можно найти из этих измерений, используя связь E и φ.

<62 63 646566 67 68 >

Дата добавления: 2015-03-03; просмотров: 1517;