Понятие о мультиполе

Диполь является частным случаем системы электрических заря­дов, обладающей определенной симметрией. Можно указать еще примеры симметричных систем зарядов (рис. 12.13). Общее название подобных распределений зарядов — электрические мультиполи.

Они бывают разных порядков (l = 0, 1, 2 и т. д.), число зарядов мультиполя определяется выра­жением 2¹. Так, мультиполем нулевого порядка, (2° = 1) является одиночный точечный заряд (рис. 12.13, а), мультиполем первого порядка (2¹ = 2) — диполь, мультиполем второго порядка (2² = 4) — квадруполь (рис. 12.13, б), мульти­полем третьего порядка (2³ = 8) — октуполь (рис. 12.13, в) и т. д.

Потенциал поля мультиполя убывает на значи­тельных расстояниях r от него пропорционально 1/r^{l + 1}. Так, для заряда (l = 0) φ ~ 1/r, диполя (1 = 1) φ ~ 1/г², для квадруполя (l = 2) φ ~1/г³ и т. д.

Если заряд распределен в некоторой области пространства, то потенциал электрического поля в любой точке А вне системы за­рядов можно представить в виде некоторого приближенного ряда:

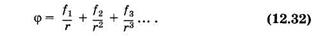
Здесь г расстояние от системы зарядов до точки А с потенциалом φ; f₁, f_2, f_{3, …}— некоторые функции, зависящие от вида мультиполя, его зарядов и от направления на точку А. Первое слагаемое (12.32) соответствует монополю, второе — диполю, третье — квадруполю и т. д. В случае нейтральной системы зарядов первое слагаемое равно нулю. Если r так велико, что можно пренебречь всеми членами ряда, начиная с третьего, тогда из (12.32) получа­ем потенциал поля диполя [см. (12.27)].

§ 12.4. Дипольный электрический генератор (токовый диполь)

В вакууме или в идеальном изоляторе электрический диполь может сохраняться сколь угодно долго. Однако в реальной ситу­ации (электропроводящая среда) под действием электрического поля диполя возникает движение свободных зарядов и диполь ли­бо экранируется, либо нейтрализуется.

На основании закона Ома для полной цепи, если r >> R_1>, то I = ξ/r.

Можно заключить, что в этом случае сила тока во внешней це­пи будет оставаться почти постоянной, она почти не зависит от свойств среды (при условии r>> R₁). Такая двухполюсная система, состоящая из истока и стока тока, называется дипольным элект­рическим генератором или токовым диполем.

Между дипольным электрическим генератором и электриче­ским диполем имеется большая аналогия, которая основывается на общей аналогии электрического поля в проводящей среде и электростатического поля.

Проиллюстрируем эту аналогию на примере плоского конден­сатора.

Пусть между пластинами плоского конденсатора находится среда с удельным электрическим сопротивлением р или, иначе, с удельной электрической проводимостью γ (γ = 1/ρ). Сопротивле­ние между пластинами конденсатора, как для проводника с сече­нием S и длиной l, равно

Если сравнить (12.33) с выражением для емкости плоского конденсатора

— — — линии тока (электрическое поле в проводящей среде) совпадают с линиями напряженности электростатического поля при одинаковой форме электродов;

— — — в том и другом случаях многие формулы имеют тождественный вид, переход от одних формул к другим осуществляется заме­ной εε₀ на γ, q на I, С на G (или 1/С на R). Закон Ома G =I/U аналогичен формуле С = q/U.

Воспользуемся этой аналогией и получим выражение для токового диполя. Аналогично электрическому моменту диполя введем дипольный момент дипольного электрического генератора:

где l — расстояние между точками истока и стока тока. Потенци­ал поля дипольного электрического генератора выражается фор­мулой, аналогичной (12.27):

По существу, электрический мультипольный генератор — это некоторая пространственная совокупность электрических токов (совокупность истоков и стоков различных токов).

Все, что было сказано выше о потенциалах полей системы за­рядов (электростатическое поле), справедливо и для такого гене­ратора (токового мультиполя) в слабо проводящей среде.