Модели непоршневого вытеснения нефти водой
Все известные методики расчета процесса разработки нефтяных месторождений с учетом непоршневого характера вытеснения нефти водой основаны на теории совместной фильтрации неоднородных жидкостей. Поясним ее вначале на примере вытеснения нефти водой из прямолинейного однородного пласта. Этот пример соответствует случаю вытеснения нефти водой из элемента однорядной схемы расположения скважин, происходящему в сечениях элемента, находящихся на значительном удалении от самих скважин, где характер движения вытесняемой и вытесняющей жидкостей близок к прямолинейному.
Рассматривая непоршневое вытеснение нефти водой в прямолинейном пласте, выделим элемент длиной 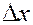 , высотой
, высотой 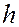 и шириной b в направлении, перпендикулярном к плоскости (рис. 46).
и шириной b в направлении, перпендикулярном к плоскости (рис. 46).
 |
Рис.46 Схема элемента пласта при непоршневом
вытеснении нефти водой
В общем случае слева в элемент пласта поступают, а справа вытекают нефть и вода. При этом расход воды слева равен 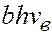 , а справа
, а справа 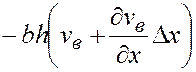 .
.
Количество накопленной воды в элементе пласта составляет
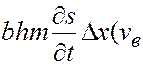 — скорость фильтрации воды;
— скорость фильтрации воды; 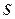 — водонасыщенность пласта;
— водонасыщенность пласта; 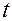 — время). Согласно закону сохранения массы вещества, разность между скоростями входящей в элемент пласта воды и выходящей из него равна скорости накопления объема воды в элементе пласта. Выражая сказанное в математической форме, получим
— время). Согласно закону сохранения массы вещества, разность между скоростями входящей в элемент пласта воды и выходящей из него равна скорости накопления объема воды в элементе пласта. Выражая сказанное в математической форме, получим
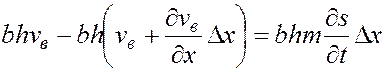 .
.
После сокращения соответствующих членов при устремлении 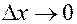 имеем
имеем
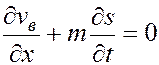 . (5.43)
. (5.43)
Поскольку в пористой среде содержатся только нефть и вода, то насыщенность пористой среды нефтью 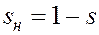 . Рассматривая аналогично предыдущему скорости проникновения нефти в элемент пласта и выхода из него, получим
. Рассматривая аналогично предыдущему скорости проникновения нефти в элемент пласта и выхода из него, получим
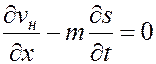 . (5.44)
. (5.44)
Складывая уравнения (5.43) и (5.44), имеем
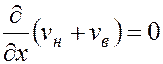 ;
; 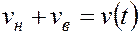 . (5.45)
. (5.45)
Таким образом, суммарная скорость фильтрации нефти и воды не изменяется по координате 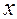 , что и следовало ожидать, так как нефть и воду принимают за несжимаемые жидкости.
, что и следовало ожидать, так как нефть и воду принимают за несжимаемые жидкости.
Следовательно, режим пласта жесткий водонапорный.
Скорости фильтрации воды и нефти подчиняются обобщенному закону Дарси, так что
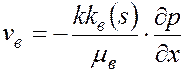 ;
; 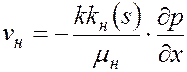 , (5.46)
, (5.46)
где 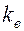 и
и 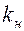 ,
, 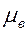 и
и 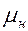 — относительные проницаемости, зависящие от водонасыщенности
— относительные проницаемости, зависящие от водонасыщенности 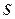 и вязкости воды и нефти.
и вязкости воды и нефти.
Рассмотрим функцию 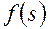 , называемую функцией Бакли- Леверетта. При этом
, называемую функцией Бакли- Леверетта. При этом
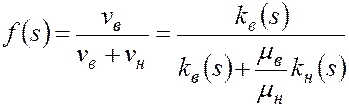 , (5.47)
, (5.47)
или
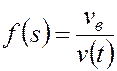 . (5.48)
. (5.48)
Из (6.48), дифференцируя 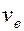 по
по 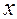 , получим
, получим
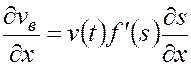 . (5.49)
. (5.49)
После подстановки (5.49) в (5.43) получим одно дифференциальное уравнение первого порядка для определения 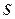 , т. е.
, т. е.
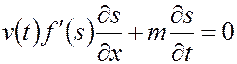 . (5.50)
. (5.50)
По мере вытеснения нефти водой из прямолинейного пласта фронт вытесняющей нефть воды продвигается к концу пласта и водонасыщенность в каждом сечении заводненной области непрерывно увеличивается. Процесс вытеснения нефти водой из прямолинейного пласта можно представить и иным образом, следя за изменением по пласту некоторой водонасыщенности. Если, например, в какой-то момент времени в некотором сечении пласта водонасыщенность составляла 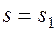 , то спустя определенное время эта водонасыщенность будет и в конце пласта, так как нефть постепенно извлекается из него и ее место занимает вода. Для указанного
, то спустя определенное время эта водонасыщенность будет и в конце пласта, так как нефть постепенно извлекается из него и ее место занимает вода. Для указанного 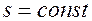 можно принять
можно принять
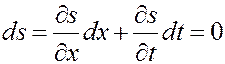
или
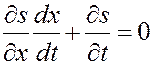 (5.51)
(5.51)
Сравним (5.50) и (5.51). Они будут идентичными, если положить
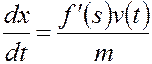 . (5.52)
. (5.52)
Умножим и разделим (5.52) на 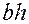 и проинтегрируем, получим
и проинтегрируем, получим
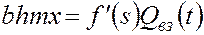 ;
; 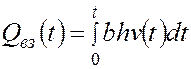 . (5.53)
. (5.53)
Обозначим
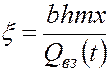 , (5.54)
, (5.54)
тогда
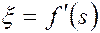 . (5.55)
. (5.55)
Задавая 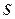 в формуле (5.55), можно определить расстояние от входа в пласт для данного значения водонасыщенности. Однако в период безводной эксплуатации закачиваемая вода еще не достигает конца пласта. Чтобы установить положение фронта вытеснения нефти водой и водонасыщенность на фронте вытеснения, рассмотрим материальный баланс закачанной в пласт воды. Если к моменту времени
в формуле (5.55), можно определить расстояние от входа в пласт для данного значения водонасыщенности. Однако в период безводной эксплуатации закачиваемая вода еще не достигает конца пласта. Чтобы установить положение фронта вытеснения нефти водой и водонасыщенность на фронте вытеснения, рассмотрим материальный баланс закачанной в пласт воды. Если к моменту времени 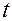 в пласт закачан объем воды, равный
в пласт закачан объем воды, равный 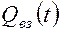 , длина фронта вытеснения составит
, длина фронта вытеснения составит 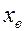 , насыщенность пласта связанной водой
, насыщенность пласта связанной водой 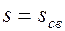 , то
, то
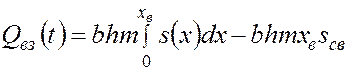 . (5.56)
. (5.56)
Введем следующие обозначения:
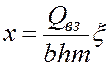 ;
; 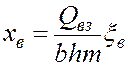 ;
; 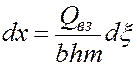 . (5.57)
. (5.57)
Тогда, подставляя (5.57) в (5.56), получим
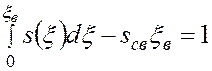 . (5.58)
. (5.58)
Поскольку 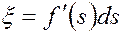 , то
, то
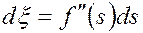 .
.
Следовательно, из (5.58)
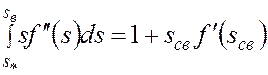 . (5.59)
. (5.59)
В выражении (5.59) принято, что при 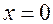 и
и 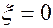 , т. е. на входе в пласт, мгновенно устанавливается водонасыщенность
, т. е. на входе в пласт, мгновенно устанавливается водонасыщенность 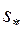 , при которой
, при которой 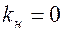 , а на фронте вытеснения значение ее в течение всего процесса составит
, а на фронте вытеснения значение ее в течение всего процесса составит 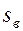 .
.
Выполним интегрирование в левой части (6.59) по частям. Имеем
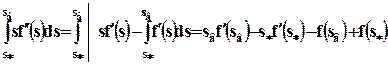 (5.60)
(5.60)
В соответствии со сказанным водонасыщенность 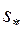 устанавливается в сечении
устанавливается в сечении 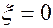 . Следовательно,
. Следовательно, 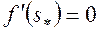 , поэтому и второй член в формуле (5.60) равен нулю. Далее, поскольку
, поэтому и второй член в формуле (5.60) равен нулю. Далее, поскольку 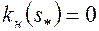 , то, согласно формуле (5.47),
, то, согласно формуле (5.47), 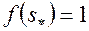 . Таким образом, из (5.59) и (5.60) получим
. Таким образом, из (5.59) и (5.60) получим
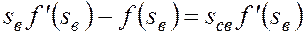 ,
,
откуда
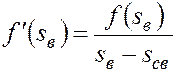 . (5.61)
. (5.61)
На рис. 47 приведен график, построенный с учетом кривых относительных проницаемостей, данных на рис. 40, при 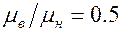 .
.
 По кривой
По кривой 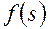 можно найти значение
можно найти значение 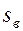 , графическим путем. В самом деле, согласно рис. 47
, графическим путем. В самом деле, согласно рис. 47

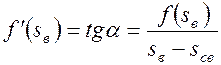 .
.
Рис.47. График зависимости
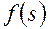 от S от S
| Рис.48. График зависимости 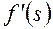 от S от S
|
Проведя касательную к кривой 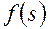 из точки
из точки 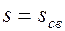 , по точке касания (см. рис. 47) определяем
, по точке касания (см. рис. 47) определяем 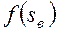 и
и 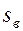 .
.
Для того же, чтобы найти распределение водонасыщенности по длине пласта, необходимо построить кривую 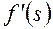 (рис. 48). Это можно сделать методом графического дифференцирования кривой
(рис. 48). Это можно сделать методом графического дифференцирования кривой 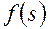 или, представив кривые относительных проницаемостей аналитически, выполнить дифференцирование аналитическим путем, сделав соответствующее построение.
или, представив кривые относительных проницаемостей аналитически, выполнить дифференцирование аналитическим путем, сделав соответствующее построение.
Определим теперь длительность безводного периода добычи нефти, т. е. момент времени 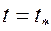 , когда фронт вытеснения достигнет конца пласта и, следовательно,
, когда фронт вытеснения достигнет конца пласта и, следовательно, 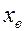 будет равен
будет равен 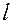 .
.
Будем считать, что к этому моменту времени в пласт закачано 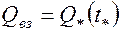 воды. Имеем из (5.57)
воды. Имеем из (5.57)
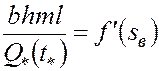 . (5.62)
. (5.62)
Из (5.62) определим 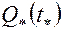 и, следовательно,
и, следовательно, 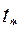 . Величина
. Величина 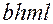 равна объему
равна объему 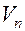 пор пласта. Так как режим жесткий водонапорный, объем закачанной в пласт воды к моменту времени
пор пласта. Так как режим жесткий водонапорный, объем закачанной в пласт воды к моменту времени 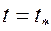 равен объему добытой из пласта нефти
равен объему добытой из пласта нефти 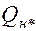 к этому же моменту времени, т.е.
к этому же моменту времени, т.е. 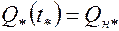 . Безводная нефтеотдача
. Безводная нефтеотдача 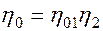 , где
, где 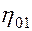 - коэффициент вытеснения нефти водой, достигнутый в безводный период. Поэтому
- коэффициент вытеснения нефти водой, достигнутый в безводный период. Поэтому
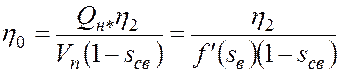 . (5.63)
. (5.63)
Заметим, что распределение водонасыщенности в пласте изменяется по мере продвижения в глубь пласта фронта вытеснения нефти водой таким образом, что значения 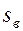 на фронте вытеснения
на фронте вытеснения 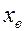 и
и 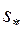 на входе в пласт остаются неизменными. Таким образом, кривая распределения водонасыщенности как бы «растягивается», оставаясь подобной себе. Такое распределение некоторого параметра, будь то водонасыщенность или какой-либо другой параметр, называется автомодельным. Соответствующие решения задач также именуются автомодельными.
на входе в пласт остаются неизменными. Таким образом, кривая распределения водонасыщенности как бы «растягивается», оставаясь подобной себе. Такое распределение некоторого параметра, будь то водонасыщенность или какой-либо другой параметр, называется автомодельным. Соответствующие решения задач также именуются автомодельными.
Полученные формулы позволяют рассчитать распределение водонасыщенности к моменту подхода воды к линии добывающих скважин, т. е. в безводный период разработки пласта.
Однако добыча нефти из пласта продолжается и после прорыва фронта вытеснения к концу пласта при 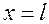 .
.
 Рис.49. Схема вытеснения нефти водой из прямолинейного пласта в водный период разработки.
Рис.49. Схема вытеснения нефти водой из прямолинейного пласта в водный период разработки.
Распределение водонасыщенности: 1-истинное; 2-фиктивное
Для определения текущей нефтеотдачи и обводненности продукции при 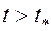 , т.е. в водный период разработки пласта поступим следующим образом. Будем считать, что продвижение фронта вытеснения происходит и в водный период разработки пласта, но этот фронт распространяется вправо за пределы пласта (рис. 49). Водонасыщенность на таком фиктивном фронте вытеснения и в этом случае остается постоянной, равной
, т.е. в водный период разработки пласта поступим следующим образом. Будем считать, что продвижение фронта вытеснения происходит и в водный период разработки пласта, но этот фронт распространяется вправо за пределы пласта (рис. 49). Водонасыщенность на таком фиктивном фронте вытеснения и в этом случае остается постоянной, равной 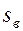 , а водонасыщенность при
, а водонасыщенность при 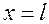 уже составит
уже составит 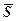 . Пусть в некоторый момент времени
. Пусть в некоторый момент времени 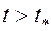 фиктивный фронт находится на расстоянии
фиктивный фронт находится на расстоянии 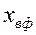 от входа в пласт (см. рис. 49). В соответствии с формулами (5.54) и (5.55) при
от входа в пласт (см. рис. 49). В соответствии с формулами (5.54) и (5.55) при 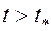 можно написать
можно написать
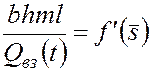 . (5.64)
. (5.64)
Из (5.62) и (5.64) получим
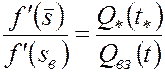 . (5.65)
. (5.65)
По формуле (5.65) находим 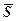 для различных значений времени
для различных значений времени 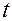 . Так, зная
. Так, зная 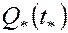 ,
, 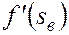 и
и 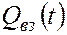 , определим вначале
, определим вначале 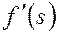 , а затем по графику функции
, а затем по графику функции 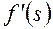 - значение
- значение 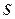 .
.
Дебиты нефти и воды в водный период разработки пласта составят
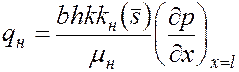 ;
; 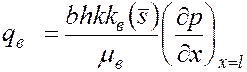 . (5.66)
. (5.66)
Отсюда для определения текущей обводненности продукции 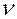 получим формулу
получим формулу
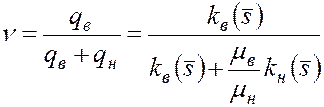 . (5.67)
. (5.67)
Текущую нефтеотдачу в водный период разработки пласта можно определить в принципе следующим образом:
1) установлением объема накопленной добычи нефти по формуле
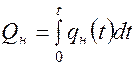 ;
;
2) отнесением этого объема накопленной добычи нефти к первоначальному объему нефти в пласте, равному 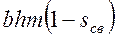 .
.
Однако во втором случае можно определять объем добытой из пласта нефти по изменению в нем водонасыщенности, учитывая опять-таки то, что режим разработки пласта жесткий водонапорный. Так, на основе равенства объема вошедшей в пласт воды объему вытесненной из него нефти имеем
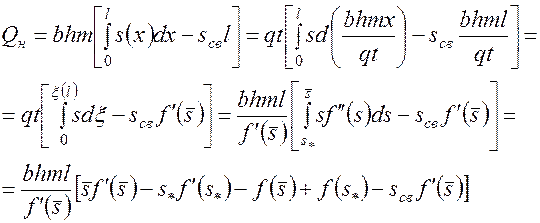 (5.68)
(5.68)
Формула (5.68) должна быть справедлива для всех моментов времени, когда 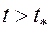 . При
. При 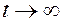 , вообще говоря, водонасыщенность должна стать равной
, вообще говоря, водонасыщенность должна стать равной 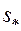 во всем пласте. Однако при любом другом значении времени водонасыщенность
во всем пласте. Однако при любом другом значении времени водонасыщенность 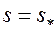 только на входе в пласт, т. е. при
только на входе в пласт, т. е. при 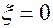 . Тогда, как следует из формулы (13),
. Тогда, как следует из формулы (13), 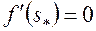 . Следовательно, из (5.68) получим
. Следовательно, из (5.68) получим
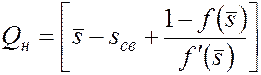 . (5.69)
. (5.69)
| ~ |
Из (5.69) вытекает, что текущая нефтеотдача пласта в период водной его эксплуатации
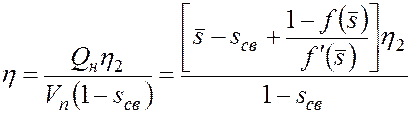 . (5.70)
. (5.70)
Таким образом, мы определили основные технологические указатели разработки элемента пласта — текущую нефтеотдачу и обводненность добываемой продукции.
Рассмотрим непоршневое вытеснение нефти водой в радиальном направлении, например, при разработке элемента семиточечной системы с использованием заводнения. Схема элементарного объема пласта для такого случая показана на рис. 50. Уравнение неразрывности фильтрующейся воды в таком объеме получим с учетом баланса втекающей и вытекающей воды за время 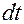 в виде
в виде
 Рис.50. Схема элементарного объема радиального пласта
Рис.50. Схема элементарного объема радиального пласта
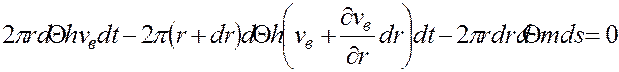 . (5.71)
. (5.71)
Раскрывая скобки в выражении (5.71), сокращая в нем соответствующие члены и заменяя обозначения обыкновенных производных на частные, имеем
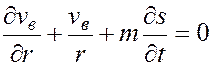
или
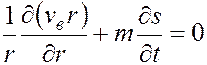 . (5.72)
. (5.72)
Вполне аналогичным образом, но с учетом того, что насыщен- ность пористой среды нефтью 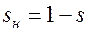 , установим соответствующее уравнение неразрывности для фильтрующейся в пласте нефти в следующем виде:
, установим соответствующее уравнение неразрывности для фильтрующейся в пласте нефти в следующем виде:
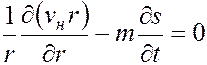 . (5.73)
. (5.73)
Складывая уравнения (5.72) и (5.73), получим
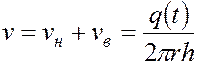 . (5.74)
. (5.74)
Вводя, как и в случае прямолинейного вытеснения нефти водой, функцию 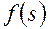 , определяемую формулой (5.47) (Бакли-Леверетта), и подставляя ее в (5.72) с учетом (5.74), будем иметь одно дифференциальное уравнение для определения водонасыщенности s в виде
, определяемую формулой (5.47) (Бакли-Леверетта), и подставляя ее в (5.72) с учетом (5.74), будем иметь одно дифференциальное уравнение для определения водонасыщенности s в виде
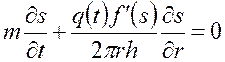 . (5.75)
. (5.75)
Так же, как и в прямолинейном случае, рассматриваем перемещение со временем в пласте линий 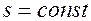 . В этом случае
. В этом случае
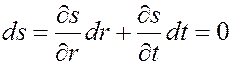 (5.76)
(5.76)
Из (5.75) и (5.76)
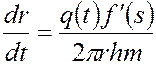 .
.
Отсюда
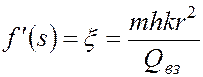 (5.77)
(5.77)
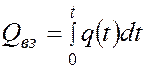 .
.
Рассмотрим баланс закачанной в пласт и извлеченной из него воды. Устремляя для простоты радиус скважины к нулю ( 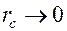 ), имеем
), имеем
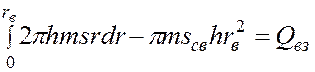 . (5.78)
. (5.78)
Учитывая, что
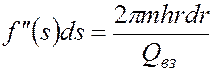 ;
; 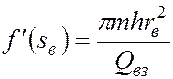 ,
,
и подставляя эти выражения в (5.78), приходим к интегральному соотношению
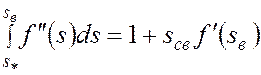 ,
,
в точности совпадающему с соответствующим соотношением (5.59) для случая вытеснения нефти водой из прямолинейного пласта. Можно поэтому утверждать, что и при вытеснении нефти водой из радиального пласта справедливы соотношение (5.60) и все последующие рассуждения, включая формулу (5.61), пригодную для нахождения водонасыщенности на фронте вытеснения нефти водой, а также описанный графический метод определения 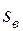 .
.
Время 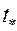 безводной разработки пласта радиусом
безводной разработки пласта радиусом 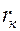 определим из (5.77). Если полагать, что
определим из (5.77). Если полагать, что 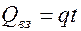 , имеем
, имеем
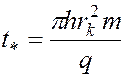 . (5.79)
. (5.79)
Аналогично по формулам (5.66) и (5.67) находим текущую обводненность 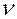 продукции, добываемой из пласта при
продукции, добываемой из пласта при 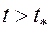 . Соответственно текущую нефтеотдачу
. Соответственно текущую нефтеотдачу 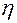 вычислим по формуле (5.70). Таким образом, определяем все важнейшие технологические показатели процесса вытеснения нефти водой.
вычислим по формуле (5.70). Таким образом, определяем все важнейшие технологические показатели процесса вытеснения нефти водой.
Дата добавления: 2015-02-28; просмотров: 1931;
